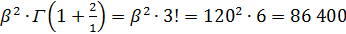Теоретическая часть.
Поле – скалярная функция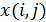 
, заданная на плоскости, где 
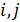– декартовы координаты. Если 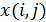есть случайная функция, то поле является случайным. Для двумерной сетки 
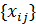есть совокупность случайных величин, как правило, взаимно зависимых. Простейшие модели случайных полей используют взаимно независимые случайные величины.
Случайное поле называется гауссовским, если оно описывается совместным гауссовским распределением вероятностей для совокупности 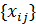. В противном случае поле являются негауссовским.
Основные характеристики одномерных распределений:
1. статистический момент – числовая харастеристика распределения данной случайно величины:
1.1. начальные моменты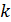 
-го порядка (
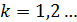) равны 
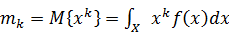, где 
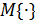- оператор математического ожидания: 
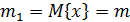является первым начальным моментом и математическим ожиданием случайной величины 
; 
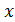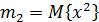– второй начальный момент и называется мощностью 
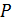случайной величины. В общем случае полное описание одномерной плотности вероятности возможно лишь бесконечной последовательностью начальных моментов.
1.2. центральные моменты 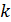-го порядка 
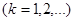равны 
: 
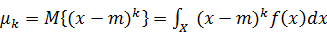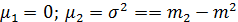– дисперсия (мощность флуктуаций (случайных изменений) есть полная мощность минус мощность постоянной составляющей).
2. среднеквадратическое отклонение (СКО)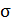 
- характеристика рассеяния случайной величины относительно её математического ожидания
3. кумулянты 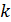-го порядка 
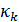- производные 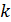-го порядка логарифма характеристической функции 
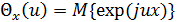в точке 
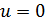, т. е. 
.
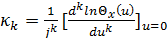4. кумулянтные коэффициенты – безразмерные коэффициенты, используемые для описания формы кривой распределения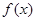 
: 
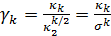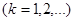, . Очевидно, 
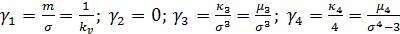и так далее. Обычно рассматриваются лишь два старших кумулянтных коэффициента: 
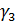– коэффициент асимметрии, 
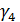– коэффициент эксцесса;
5. функция распределения – вероятность того, что случайная величина Х примет значение меньшее или равное х, где х – произвольное действительное число;
6. плотность вероятности – один из способов задания вероятностной меры (числовой характеристики события) на евклидовом пространстве (пространство с размерностью 3, которое описывается аксиомами евклидовой геометрии)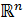 
.
Основные модельные распределения вероятности.
1. Равномерное распределение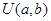 
задается на отрезке 
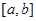, где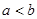 
и имеет на этом отрезке постоянное значение плотности вероятности, равное 
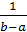. Статистические моменты даются формулой 
, 
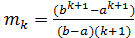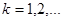. Если 
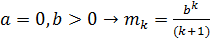. В частности, 
, 
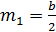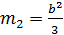, дисперсия 
.
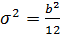2. Нормальное (гауссовское) распределение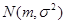 
имеет плотность вероятности 
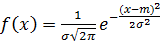, где математическое ожидание 
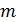и дисперсия 
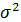являются параметрами распределения. Все кумулянтные коэффициенты, начиная с третьего, равны нулю.
3. Распределение Вейбулла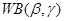 
с параметром масштаба 
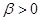и параметром формы 
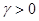имеет плотность вероятности 
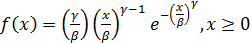. Начальные моменты распределения определяются выражением 
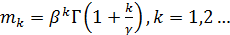, где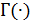 
– гамма-функция, 
, 
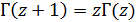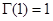. Для целых аргументов 
.
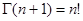3.1.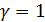 
- распределение Вейбулла переходит в экспоненциальное распределение 
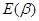с плотностью вероятности 
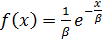. У этого распределения математическое ожидание и дисперсия равны соответственно 
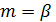и 
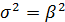. Коэффициент вариации равен единице, коэффициенты асимметрии и эксцесса равны 
, 
.
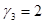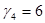3.2.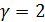 
- распределение Вейбулла переходит в распределение Релея 
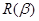с плотностью вероятности 
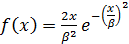, у которого математическое ожидание и второй момент равны 
, 
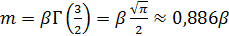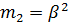. Дисперсия распределения 
.
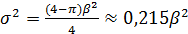4. Логарифмическое нормальное распределение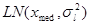 
имеет плотность (для 
) 
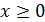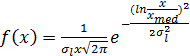, где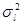 
есть дисперсия величины 
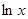. Математическое ожидание и дисперсия равны 
, 
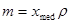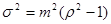, где отношение математического ожидания к медиане 
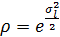. Начальные моменты логарифмического нормального распределения равны 
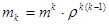. Распределение является двухпараметрическим. Медиана является параметром масштаба, а в качестве параметра формы можно выбрать 
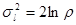, отношение математического ожидания к медиане 
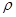, или квадрат коэффициента вариации 
.
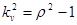Кумулянтные коэффициенты (всегда положительны, т.к.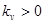 
) 
, 
.
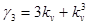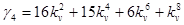Программное обеспечение, используемое в данной лабораторной работе для моделирования случайных полей, позволяет получать выборочные оценки математического ожидания, дисперсии, коэффициентов асимметрии и эксцесса, которые вычисляются по следующим формулам: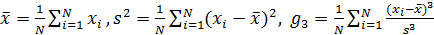 
, 
.
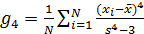Задание размера выборки N осуществляется вводом количества строк анализируемого поля (каждая строка содержит 256 выборок) в соответствующем окне изображения, т. 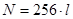е. 
, где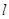 
– количество первых строк поля.
Практическая часть.
I. Выбор параметров.
Для моделирования типовых распределений по условию задания к лабораторной работе необходимо расположить гауссовское (нормальное) и непрерывное равномерное распределения в области положительных значений.
Для нормального распределения это достигается смещением центра рассеивания m (математическое ожидание M[X]=m) по шкале значений окна 2 в б о льшую сторону и уменьшением С.К.О., которое вызывает «заострение» пика распределения.
Были выбраны следующие значения математического ожидания и С.К.О. для гауссовского распределения:
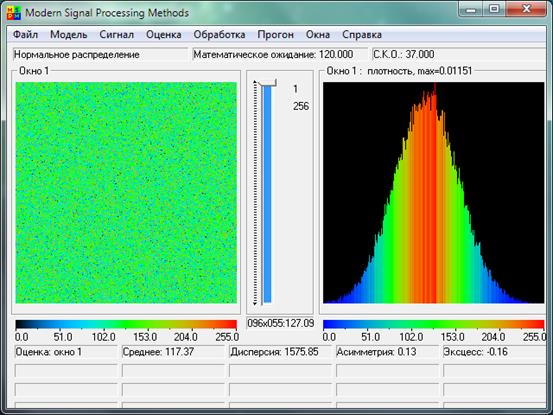
Рис. 1. Нормальное распределение с m=120, С.К.О.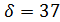 
; гистограмма по 256 строкам; объем выборки оценки 1 строка.
Исходя из того, что m=120, рассчитаем математические ожидания и дисперсии типовых распределений.
1) гауссовское (нормальное) распределение:
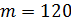
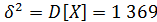
2) непрерывное равномерное распределение:
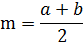
Пусть а=0, b>0, тогда:
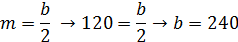
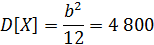
3) распределение Рэлея (распределение Вейбулла с параметром формы ):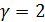
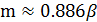
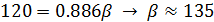- параметр масштаба
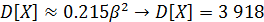
4) экспоненциальное распределение (распределение Вейбулла с параметром формы )::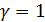
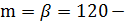параметр масштаба
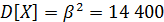
После выбора (подсчета) значений математических ожиданий и дисперсий подсчитаем мощность каждого распределения, для гауссовского распределения выражая её из формулы D[X]=m2-m2, где m2 есть математическое ожидание второго порядка и полная мощность; m – математическое ожидание первого порядка и мощность постоянной составляющей:
1) для нормального распределения:
m2=D[X]+m2=1 369+14 400=15 769
2) для равномерного распределения:
m2=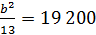 
3) для распределения Рэлея:
m2=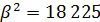 
4) для экспоненциального распределения:
m2= 