Поверхность теплопередачи каждого корпуса выпарной установки определяют по основному уравнению теплопередачи
Для определения тепловых нагрузок Q, коэффициентов теплопередачи k и полезных разностей температур Δt необходимо знать распределение упариваемой воды, концентраций растворов и их температур кипения по корпусам. Эти величины находятся методом последовательных приближений.
Производительность установки по выпариваемой воде определяют из уравнений материального баланса:
[1]
• Концентрации упариваемого раствора
Распределение концентраций раствора по корпусам установки зависит от соотношений нагрузок по выпариваемой воде в каждом аппарате.
На основании практических данных принимают, что производительность каждого корпуса по выпариваемой воде определяется соотношением: w 1 : w 2 : w 3 = 1,0: 1,1: 1,2. Тогда:
Далее рассчитывают концентрации растворов в корпусах:
Концентрация раствора в последнем корпусе x3 соответствует заданной концентрации упариваемого раствора хк.
• Температуры кипения растворов
Общий перепад давлений в установке равен:
[1]
В первом приближении общий перепад давлений распределяют между корпусами поровну. Тогда давления греющих паров в корпусах равны:
Давление пара в барометрическом конденсаторе:
[1]
что соответствует заданному значению PБ.К. (PБ.К = 0,12 атм = 0,012 МПа).
По давлению паров находим их температуры и энтальпии:
Таблица 1.
| Давление Р, МПа | Температура t, оС | Энтальпия h’’ г.п., кДж/кг | Энтальпия h’ конд, кДж/кг | Теплота парообразования r, кДж/кг |
| PГ.1. = 0,7 | tГ.1. = 164,96 | 2763,41 | 697,154 | 2066,26 |
| PГ.2. = 0,471 | tГ.2. = 149,47 | 2745,74 | 629,97 | 2115,77 |
| PГ.3. = 0,242 | tГ.3. = 126,37 | 2715,426 | 530,89 | 2184,54 |
| PБ.К. = 0,012 | tБ.К. = 48,66 | 2589,7 | 203,744 | 2385,9 |
Температура кипения раствора в корпусе отличается от температуры греющего пара в последующем корпусе на сумму температурных потерь ∑∆ от температурной (∆'), гидростатической (∆'') и гидродинамической (∆''') депрессий (∑∆=∆'+∆''+∆''').
Гидродинамическая депрессия обусловлена потерей давления пара на преодоление гидравлических сопротивлений трубопроводов при переходе из корпуса в корпус. Обычно в расчётах принимают
∆'''= 1,0 - 1,5 град на корпус. Примем для каждого корпуса ∆'''=1 град. Тогда температуры вторичных паров в корпусах будут равны:
Сумма гидродинамических депрессий:
По температурам вторичных паров определим их давления
Таблица 2
| Температура, ˚С | Давление, Мпа |
| tв.п.1. = 150,47 | Pв.п.1. = 0,489 |
| tв.п.2. = 127,37 | Pв.п.2. = 0,25 |
| tв.п.3. = 49,66 | Pв.п.3. = 0,0127 |
Гидростатическая депрессия обусловлена разностью давлений в среднем слое кипящего раствора и на его поверхности. Давление в среднем слое кипящего раствора каждого корпуса определяется по уравнению:
[2]
где Рвп - давление вторичного пара в корпусе, Па; H - высота кипятильных труб в аппарате, м; - плотность кипящего раствора, кг/м 3; - паронаполнение (объёмная доля пара в кипящем растворе), м3/м3.
Для выбора значения H необходимо ориентировочно оценить поверхность теплопередачи выпарного аппарата Fор. При кипении водных растворов можно принять удельную тепловую нагрузку аппаратов с естественной циркуляцией q = 20 000 50 000 Вт/м2. Примем q = 30 000 Вт/м2. Тогда поверхность теплопередачи 1-го корпуса ориентировочно равна:
где r1 - теплота парообразования вторичного пара, Дж/кг.
По приложению 4.2 [1] – ГОСТ 11987-81 выбираем аппарат с естественной циркуляцией, с соосной греющей камерой и кипением раствора в трубах (тип I).
Принимаем высоту кипятильных труб Н = 4 м, при диаметре труб d = 38 мм и толщине стенки ст = 2 мм.
При пузырьковом (ядерном) режиме кипения паронаполнение составляет = 0,4 0,6. Примем = 0,5. Плотность растворов NaCl при температуре 15˚С и соответствующих концентрациях в корпусах равна:
1 = 1010,02 (кг/м3);
2 = 1018,84 (кг/м3);
3 = 1234,6 (кг/м3)
При определении плотности растворов в корпусах пренебрегаем изменением её с повышением температуры от 15 ˚С до температуры кипения ввиду малого значения коэффициента объёмного расширения и ориентировочно принятого значения.
Давления в среднем слое кипятильных труб корпусов равны:
Этим давлениям соответствуют следующие температуры кипения и теплоты испарения растворителя:
Таблица 3
| Давление, МПа | Температура, ˚С | Теплота испарения, кДж/кг |
| P1.ср. = 0,4964 | t1.ср. = 151,56 | rвп.1. = 2109,34 |
| P2.ср. = 0,258 | t2.ср. = 128,46 | rвп.2. = 2178,54 |
| P3.ср. = 0,0218 | t3.ср. = 61,69 | rвп.3. = 2354,3 |
Гидростатическая депрессия по корпусам:
[2]
Сумма гидростатических депрессий равна:
[2]
Температурная депрессия ∆' определяется по уравнению:
[3]
где T - температура паров в среднем слое кипятильных труб, K; ∆'атм- температурная депрессия при атмосферном давлении.
По таблице теплофизических свойств раствора хлорида натрия и заданным концентрациям находим:
для 1-го корпуса ∆'атм = 0,685 (˚С)
для 2-го корпуса ∆'атм =0,78 (˚С)
для 3-го корпуса ∆'атм =9,6 (˚С)
Тогда температурная депрессия по корпусам равна:
Сумма температурных депрессий ∑∆'=0,95+0,93+7,4=9,28 (˚С)
Температуры кипения растворов в корпусах:
• Полезная разность температур
Общая полезная разность температур равна:
[2]
Полезные разности температур по корпусам (в °С) равны:
[2]
Тогда общая полезная разность температур:
Проверяем общую полезную разность температур:
Полезные разности температур отличаются менее чем на1 ˚С.
• Определение тепловых нагрузок
Совместным решением уравнений тепловых балансов по корпусам и уравнения балансов по воде для всей установки, определяем расход греющего пара в 1-ом корпусе, производительность каждого корпуса по выпариваемой воде и тепловые нагрузки по корпусам.
где Q1, Q2, Q3 – тепловые нагрузки по корпусам, кВт; D – расход греющего пара в 1-ом корпусе, кг/с; 1,03 – коэффициент, учитывающий 3% потерь тепла в окружающую среду; h''г.1.., h''г.2., h''г.3. - энтальпии греющих паров по корпусам кДж/кг; h''вп.1., h''вп.2., h''вп.3. - энтальпии вторичных паров по корпусам кДж/кг; h'1, h'2, h'3 – энтальпии конденсата по корпусам, кДж/кг; св – теплоёмкость воды кДж/кг.К; сн, с1, с2 – теплоёмкости раствора начальной концентрации в первом корпусе и втором корпусе, соответственно, кДж/кг,К; tн, tк.1., tк.2.– температура кипения исходного раствора при давлении в 1-ом корпусе и температуры кипения растворов по корпусам соответственно, оС
°C (где ∆'н – температурная депрессия исходного раствора); Q1.конц., Q2.конц., Q3.конц. – теплота концентрирования по корпусам, кВт; принимаем Q1.конц. = Q2.конц. = =Q3.конц. = 0, так как при концентрировании раствора NaCl теплота не поглощается, а выделяется. Таким образом, выделившееся количество теплоты идёт в запас.
Полученные расходы незначительно отличаются от принятого распределения. Т.к. погрешность не превышает 3%, пересчёт нагрузок не производится. Используя эти данные, найдём:
Q1 = 1942,28 (кВт)
Q2 = 1777,25 (кВт)
Q3 =2009,77 (кВт)
Результаты расчёта сведены в таблицу:
Таблица 4
| Наименование параметра | 1-й корпус | 2-й корпус | 3-й корпус |
| Производительность по упариваемой воде w, кг/с. | 0,84 | 0,92 | 0,95 |
| Концентрация растворов х, % | 1,4 | 2,6 | |
| Давление греющих паров Pг, Мпа | 0,7 | 0,471 | 0,242 |
| Температура греющих паров tг, ˚C | 164,96 | 149,47 | 126,37 |
| Температурные потери, град | 2,54 | 3,02 | 20,43 |
| Температура кипения раствора tк, ˚C | 152,01 | 129,39 | 69,09 |
| Полезная разность температур tп, град | 12,95 | 20,08 | 57,28 |
• Выбор конструкционного материала
Выбираем конструкционный материал, стойкий к среде кипящего раствора NaCl в интервале изменения концентраций от 1,0 до 30%. В этих условиях химически стойкой является сталь марки Х17, имеющая скорость коррозии не менее 0,1 мм в год, коэффициент теплопроводности ст = 25,1 Вт/(м.К).
• Расчёт коэффициентов теплопередачи
Коэффициент теплопередачи для первого корпуса определяют по уравнению аддитивности термических сопротивлений:
[4]
Примем, что суммарное термическое сопротивление равно термическому сопротивлению стенки δст/λст и накипи δн/λн. Термическое сопротивление загрязнений со стороны пара не учитываем. Получим:
Коэффициент теплоотдачи от конденсирующегося пара к стенке α1 равен:
[2]
где r1 - теплота конденсации греющего пара, Дж/кг; ρж, λж, μж - соответственно плотность (кг/м 3), теплопроводность Вт/(м·К), вязкость (Па·с) конденсата при средней температуре плёнки, t пл= t г.1. – ∆ t 1/2, где ∆ t 1 - разность температур конденсации пара и стенки, град.
Первый корпус
Расчёт ∆ t 1 ведут методом последовательных приближений. В первом приближении примем ∆ t 1=2 град. Тогда:
r1 =2063,1 кДж/кг ρж = 889 кг/м3
μж = 15,09∙10-5 Па∙с λж = 0,674Вт/(м∙К)
Для установившегося процесса передачи тепла справедливо уравнение:
где q - удельная тепловая нагрузка, Вт/м 2; Δtст - перепад температур на стенке, град; Δt2 - разность между температурой стенки со стороны раствора и температурой кипения раствора.
Отсюда:
[2]
Тогда:
[2]
Коэффициент теплоотдачи от стенки к кипящему раствору в условиях его естественной циркуляции для пузырькового режима в вертикальных трубах равен:
, [2]
где – плотность греющего пара в первом корпусе, – плотность пара при атмосферном давлении; – соответственно, теплопроводность, поверхностное натяжение, теплоемкость и вязкость раствора в первом корпусе.
Физические свойства кипящего раствора NaCl сведём в таблицу 5:
Таблица 5
| Параметр | Корпус | ||
| Теплопроводность λ, Вт/(м·К) [3] | 0,7 | 0,693 | 0,644 |
| Плотность растворов ρ, кг/м [3] | 955,12 | 965,88 | 1072,2 |
| Теплоемкость раствора с, Дж/ (кг·К)[4] | 4328,6 | 4207,6 | |
| Вязкость раствора µ·10-3, Па·с [3] | 0,3054 | 0,4638 | 0,5820 |
Скорость движения раствора принимаем равной v =2 (м/с). Подставив численные значения, получим:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' = α1∙∆t1
q' = 9885,438∙2= 19770,876Вт/м2
q'' = α2∙∆t2
q'' = 11129,7083∙4,43=49304,6078 Вт/м2
Как видим, q' ≠ q''
Расхождение между тепловыми нагрузками превышает 3%. Для второго приближения примем ∆ t 1=3 град.
Пренебрегая изменением физических свойств конденсата при изменении температуры на несколько градусов, рассчитаем α1 по соотношению:
Получим:
q' = 8932,502∙3= 26797,506Вт/м2
q'' = 11129,7083∙1,11=12353,976 Вт/м2
Как видим, q' ≠ q''
Для расчёта в третьем приближении строим графическую зависимость удельной тепловой нагрузки от разности температур между паром и стенкой в первом корпусе (рис. 1) и определяем ∆ t 1= 2,7 град. Получим:
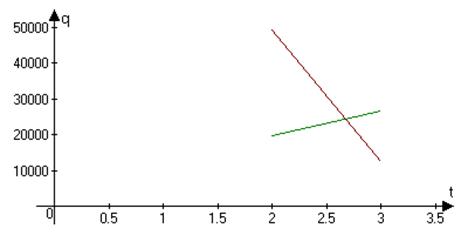
Рис. 1. Зависимость удельной тепловой нагрузки q от разности температур t в корпусе
q' = 9170,911∙2,7=24761,46 Вт/м2
q'' = 11129,7083∙2,08=23149,79Вт/м2
Как видим, q' ≈ q''
Находим коэффициент теплопередачи:
Второй корпус
Примем t = 8 ˚С. Тогда
tпл = tг.2 – ∆t1 /2
tпл = 149,47– 8/2 = 145,47 °С
r2 =2129,56 кДж/кг ρж = 915кг/м3
μж = 17,9∙10-5 Па∙с λж = 0,689 Вт/(м∙К)
Тогда:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' =2 389,26∙8 = 19114,08 Вт/м2
q'' = ∙5,772 = 20212,74 Вт/м2
Как видим, q' ≈ q''
Расхождение между тепловыми нагрузками не превышает 3%, расчёт коэффициентов теплоотдачи на этом заканчиваем.
Находим коэффициент теплопередачи:
Третий корпус
В первом приближении примем t = 19˚С. Тогда
tпл = tг.3 – ∆t1 /2
tпл = 126,37 – 19/2 = 116,87 °С
r3 =2211,9кДж/кг ρж = 940,52 кг/м3
μж = 21,53∙10-5 Па∙с λж = 0,6856 Вт/(м∙К)
Тогда:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' =3623,4∙22,72 = 82323,648 Вт/м2
q'' = 5411,203∙15,56 = 84122,54 Вт/м2
Как видим, q' ≈ q''
Расхождение между тепловыми нагрузками не превышает 3%, расчёт коэффициентов теплоотдачи на этом заканчиваем.
Находим коэффициент теплопередачи:
• Распределение полезной разности температур
Полезные разности температур в корпусах установки находим из условия равенства их поверхностей теплопередачи:
[1]
где ∆tп о, Qj, Kj - соответственно полезная разность температур, тепловая нагрузка, коэффициент теплопередачи для j- го корпуса.
Q1 =1942,28 (кВт)
Q2 = 1777,25 (кВт)
Q3 = 2009,77 (кВт)
Подставив численные значения, получим:
Проверим общую полезную разность температур установки:
Теперь рассчитаем поверхность теплопередачи выпарных аппаратов:
[1]
Найденные значения мало отличаются от ориентировочно определённой ранее поверхности Fор. Поэтому в следующих приближениях нет необходимости вносить коррективы на изменение конструктивных размеров аппаратов (высоты, диаметра и числа труб). Сравнение распределённых из условий равенства поверхностей теплопередачи и предварительно рассчитанных значений полезных разностей температур ∆tп представлено в следующей таблице.
Сравнение полезных разностей температур ∆tП, ранее принятых и в 1-м приближении, приведено ниже:
Таблица 6
| Параметр | Корпус | ||
| ∆tп в первом приближении, град. | 12,95 | 20,08 | 57,28 |
| Предварительно рассчитанные значения ∆tп, град. | 20,815 | 37,28 | 32,196 |
Как видно, полезные разности температур, рассчитанные из условия равного перепада давления в корпусах и найденные в первом приближении из условия равенства поверхностей теплопередачи в корпусах, существенно различаются. Поэтому необходимо заново перераспределить температуры между корпусами установки. В основу этого перераспределения температур будут положены полезные разницы температур, найденные из уравнений равенства поверхностей теплопередачи аппаратов.
• Уточнённый расчет
Полученные после перераспределения температур (давлений) параметры растворов и паров по корпусам представлены ниже:
Таблица 7
| Параметры | Корпус | ||
| Производительность по испаряемой воде ω, кг/с | 0,814 | 0,976 | |
| Концентрация растворов х, % | 1,4 | 2,6 | |
| Температура греющего пара tг. , °С | 164,96 | - | - |
| Полезная разность температур Δtп , град | 20,815 | 37,28 | 32,196 |
| Температура кипения раствора tк= tг -Δtп , °С | 144,145 | 112,19 | 94,174 |
| Температура вторичного пара tвп = tк – (Δ' + Δ"), °С | 142,91 | 110,17 | 74,74 |
| Давление вторичного пара Рвп, МПа | 0,39 | 0,145 | 0,038 |
| Температура греющего tг = tвп –Δ'", °С | - | 109,17 | 73,74 |
Q1 = 1942,28 (кВт)
Q2 = 1777,25 (кВт)
Q3 =2009,77 (кВт)
Первый корпус
Расчёт ∆ t 1 ведут методом последовательных приближений. В первом приближении примем ∆ t 1=2 град. Тогда:
r1 =2063,1 кДж/кг ρж = 889 кг/м3
μж = 15,09∙10-5 Па∙с λж = 0,674Вт/(м∙К)
Для установившегося процесса передачи тепла справедливо уравнение:
где q - удельная тепловая нагрузка, Вт/м 2; Δtст - перепад температур на стенке, град; Δt2 - разность между температурой стенки со стороны раствора и температурой кипения раствора.
Отсюда:
Тогда:
Коэффициент теплоотдачи от стенки к кипящему раствору в условиях его естественной циркуляции для пузырькового режима в вертикальных трубах равен:
,
где – плотность греющего пара в первом корпусе, – плотность пара при атмосферном давлении; – соответственно, теплопроводность, поверхностное натяжение, теплоемкость и вязкость раствора в первом корпусе.
Физические свойства кипящего раствора NaCl сведём в таблицу 5:
Таблица 5
| Параметр | Корпус | ||
| Теплопроводность раствора λ, Вт/(м·К) | 0,7 | 0,693 | 0,644 |
| Плотность растворов ρ, кг/м3 | 955,12 | 965,88 | 1072,2 |
| Теплоемкость раствора с, Дж/ (кг·К) | 4328,6 | 4207,6 | |
| Вязкость раствора µ·10-3, Па·с | 0,3054 | 0,4638 | 0,5820 |
Скорость движения раствора принимаем равной v =2 (м/с). Подставив численные значения, получим:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' = α1∙∆t1
q' = 9885,438∙2= 19770,876Вт/м2
q'' = α2∙∆t2
q'' = 11129,7083∙4,43=49304,6078 Вт/м2
Как видим, q' ≠ q''
Расхождение между тепловыми нагрузками превышает 3%. Для второго приближения примем ∆ t 1=3 град.
Пренебрегая изменением физических свойств конденсата при изменении температуры на несколько градусов, рассчитаем α1 по соотношению:
Получим:
q' = 8932,502∙3= 26797,506Вт/м2
q'' = 11129,7083∙1,11=12353,976 Вт/м2
Как видим, q' ≠ q''
Для расчёта в третьем приближении строим графическую зависимость удельной тепловой нагрузки от разности температур между паром и стенкой в первом корпусе (рис. 1) и определяем ∆ t 1= 2,7 град. Получим:

Рис. 1. Зависимость удельной тепловой нагрузки q от разности температур t в корпусе
q' = 9170,911∙2,7=24761,46 Вт/м2
q'' = 11129,7083∙2,08=23149,79Вт/м2
Как видим, q' ≈ q''
Находим коэффициент теплопередачи:
Второй корпус
Примем t = 8 ˚С. Тогда
tпл = tг.2 – ∆t1 /2
tпл = 149,47– 8/2 = 145,47 °С
r2 =2129,56 кДж/кг ρж = 915кг/м3
μж = 17,9∙10-5 Па∙с λж = 0,689 Вт/(м∙К)
Тогда:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' =2 389,26∙8 = 19114,08 Вт/м2
q'' = ∙5,772 = 20212,74 Вт/м2
Как видим, q' ≈ q''
Расхождение между тепловыми нагрузками не превышает 3%, расчёт коэффициентов теплоотдачи на этом заканчиваем.
Находим коэффициент теплопередачи:
Третий корпус
В первом приближении примем t = 19˚С. Тогда
tпл = tг.3 – ∆t1 /2
tпл = 126,37 – 19/2 = 116,87 °С
r3 =2211,9кДж/кг ρж = 940,52 кг/м3
μж = 21,53∙10-5 Па∙с λж = 0,6856 Вт/(м∙К)
Тогда:
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
q' =3623,4∙22,72 = 82323,648 Вт/м2
q'' = 5411,203∙15,56 = 84122,54 Вт/м2
Как видим, q' ≈ q''
Расхождение между тепловыми нагрузками не превышает 3%, расчёт коэффициентов теплоотдачи на этом заканчиваем.
Находим коэффициент теплопередачи:
• Распределение полезной разности температур
Полезные разности температур в корпусах установки находим из условия равенства их поверхностей теплопередачи:
где ∆tп о, Qj, Kj - соответственно полезная разность температур, тепловая нагрузка, коэффициент теплопередачи для j- го корпуса.
Q1 =1942,28 (кВт)
Q2 = 1777,25 (кВт)
Q3 = 2009,77 (кВт)
Подставив численные значения, получим:
Проверим общую полезную разность температур установки:
Теперь рассчитаем поверхность теплопередачи выпарных аппаратов:
Выбираем аппарат с поверхностью теплопередачи F = 63м2.
По ГОСТ 11987 – 81 выбираем выпарной аппарат со следующими характеристиками:
Таблица 9
| Номинальная поверхность теплообмена F,м2 | |
| Диаметр труб d, мм | 38x2 |
| Высота труб H, мм | |
| Диаметр греющей камеры dk, мм | |
| Диаметр сепаратора dc, мм | |
| Диаметр циркуляционной трубы dц, мм | |
| Общая высота аппарата Ha, мм | |
| Масса аппарата Ma, кг |
• Определение толщины тепловой изоляции
Толщину тепловой изоляции δн находят из равенства удельных тепловых потоков через слой изоляции от поверхности изоляции в окружающую среду:
[3]
где αв=9,3+0,058∙tст.2 - коэффициент теплоотдачи от внешней поверхности изоляционного материала в окружающую среду, Вт/(м2·К); tст.2. - температура изоляции со стороны окружающей среды (воздуха); для аппаратов, работающих в закрытом помещении, tст.2. выбирают в интервале 35-45 °С; tст.1. - температура изоляции со стороны аппарата, ввиду незначительного термического сопротивления стенки аппарата по сравнению термическим сопротивлением слоя изоляции tст.1. принимают равной температуре греющего пара; tв - температура окружающей среды (воздуха), °С; λн - коэффициент теплопроводности изоляционного материала, Вт/(м·К).
Рассчитаем толщину тепловой изоляции для 1-го корпуса:
tст.2. = 40 °С
tв = 20 °С
αв = 9,3+0,058∙40 = 11,62 Вт/(м2·К)
В качестве материала для тепловой изоляции выберем совелит (85% магнезии + 15% асбеста), имеющий коэффициент теплопроводности λ=0,09 Вт/ (м·К). Тогда:
[2]
Принимаем толщину тепловой изоляции 0,048 м и для других корпусов.
• Расчёт барометрического конденсатора
Для создания вакуума в выпарных установках обычно применяют конденсаторы смешения с барометрической трубой. В качестве охлаждающего агента используют воду, которая подается в конденсатор чаще при температуре окружающей среды (около 20 °С). Смесь охлаждающей воды и конденсата выливается из конденсатора по барометрической трубе. Для поддержания постоянства вакуума, в системе из конденсатора с помощью вакуум-насоса откачивают неконденсирующиеся газы.
Необходимо рассчитать расход охлаждающей воды, основные размеры (диаметр и высоту) барометрического конденсатора и барометрической трубы, производительность вакуум-насоса.
• Расход охлаждающей воды
Расход охлаждающей воды Gв определяют из теплового баланса конденсатора:
[4]
где - энтальпия паров в барометрическом конденсаторе, Дж/кг; tн - начальная температура охлаждающей воды, °С; tк – конечная температура смеси воды и конденсата, °С.
Разность температур между паром и жидкостью на выходе из конденсатора должна быть 3-5 град. Поэтому конечную температуру воды tк на выходе из конденсатора примем на 3 град ниже температуры конденсации паров:
tH = 20 (°C)
IБК = 2584,1 (кДж/кг)
св = 4,190(кДж/кг∙К)
Тогда:
• Диаметр конденсатора
Диаметр барометрического конденсатора dбк определяют из уравнения расхода:
, [2]
где ρ – плотность паров, кг/м3; v – скорость паров, м/с.
При остаточном давлении в конденсаторе порядка 10 4 Па скорость паров v = 15-25 м/с. Тогда
ρп = 0,098 кг/м3
Подбираем конденсатор с диаметром, равным расчетному или ближайший больший. Определяем его основные размеры. Выбираем барометрический конденсатор с диаметром:
dбк =800 мм.
• Высота барометрической трубы
В соответствии с нормами [6], внутренний диаметр барометрической трубы dбт равен 200 мм.
Скорость воды в барометрической трубе:
[2]
Высота барометрической трубы:
, [2]
где B – вакуум в барометрическом, Па; ∑ξ – сумма коэффициентов местных сопротивлений; λ – коэффициентов трения в барометрической трубе; 0,5 – запас высоты на возможное изменение барометрического давления, м.
[2]
[2]
где ξвх, ξвых - коэффициенты местных сопротивлений на входе в трубу и на выходе из неё.
Коэффициент трения λ зависит от режима течения жидкости. Определим режим течения воды в барометрической трубе:
ρв = 1000 (кг/м3). µв = 0,54·10-3 (Па∙с)
При Re = 274074 λ = 0,0065
отсюда
• Расчёт производительности вакуум-насоса
Производительность вакуум – насоса Gвозд определяется количеством газа (воздуха), который необходимо удалять из барометрического конденсатора:
где 2,5∙10 -5 – количество газа, выделяющегося из 1 кг воды; 0,01 – количество газа, подсасываемого в конденсатор через не плотности, на 1 кг паров.
Объемная производительность вакуум – насоса равна:
где R – универсальная газовая постоянная, Дж/(кмоль К); Мвозд - молекулярная масса воздуха, кг/моль(29 кг/моль); tвозд – температура воздуха, °С; Pвозд - парциальное давление сухого воздуха в барометрическом конденсаторе, Па.
Температуру воздуха рассчитывают по уравнению
Давление воздуха равно:
[2]
где Pп –давление сухого насыщенного пара (Па) при tвозд = 26,57°C. Подставив, получим:
[2]
Зная объёмную производительность Vвозд и остаточное давление, по каталогу подбираем вакуум-насос типа ВВН-6, мощностью N = 12,5 кВт.
• Конструктивный расчёт
Число нагревательных трубок диаметром 382, высотой 4 м:
[3]
где dcp = 0,036 м – средний диаметр трубки.
Толщина обечайки:
где D = 0,8 м – диаметр греющей камеры аппарата; P = 0,7 (МПа) – давление греющего пара; = 138 МН/м2 – допускаемое напряжение для стали; = 0,8 – коэффициент ослабления из-за сварного шва; Cк = 0,001(м) – поправка на коррозию.
= 0,81,3/21380,8 + 0,001 = 0,005 м.
Согласно рекомендациям принимаем толщину обечайки = 12 мм.
Выбираем опору с допускаемой нагрузкой 0,063 МН, конструкция которой приводятся на рис.3:
Рис. 3. Опора
Условные проходы штуцеров, мм:
для входа пара 500
для входа воды 50
для выхода парогазовой смеси 250
Список использованной литературы
• Касаткин А.Г. Основные процессы и аппараты химической технологии.Изд. 9-ое, М.,”Химия”, 1973, 750с.
• Дытнерский Ю. И. Основные процессы и аппараты химической технологии. Москва: 1991. 496 стр.
• Справочник химика, т. III, 1962., т У, М-Л., “Химия”, 1966, 974с.
• Каталог УКРНИИХИММАШа. Выпарные аппараты вертикальные трубчатые общего назначения. М., ЦИНТИХИМНЕФТЕМАШ, М., 1972.
• Таубман Е.И. Выпаривание. М.: Химия, 1982. 327 с.