Составление модели и выявление источников неопр-стей.

Модель – функц. зависимость, которая связывает выходные величины с входными; формула, по которой рассчитывается результат:

У = f(Х₁, …, Х_n). В свою очередь на каждую из вх-х величин влияют другие вел-ны, п.э. удобно построить диаграмму «причина – следст-вие», на кот. необх-мо нанести все источники неопр-стей:

2) Оценивание значений и станд-ных неопр-стей входных величин

Это можно сделать 2 спос-ми: 1)оцениванием неопр-сти, возник-щей от каждого отдельного ист-ка с послед-щим суммир-ем состав-щих; 2)непосредст. опред-ем сумм. вклада в неопр-сть от некот-х или всех ист-ков с использованием данных об эффективности метода в целом.

Станд. неопр-сти входных величин рассчитываются по методу А или В. От каждого источника рассчитывается неопр-сть в виде СКО.

По методу А: u(x_cx)= эту формулу используют когда получают несколько параллельных результатов. Оценку сходимости (СКО сходимости) можно взять из МВИ и тогда u(x_cx) = S_r или S_r может быть рассчитана по результатам экспериментальных исследований проведенных в лаборатории при разработке методики расчета неопр-сти: S_r = r/2,8, где r – предел повторяемости (сходимости).

По методу В: оценка неопр-сти зависит от вида распределения, которым вначале задаются. Наиболее часто используют 3 вида распределения: нормальное, треугольное, прямоугольное.

Прямоугольный закон явл-ся основным, используется когда известен интервал неточности измер-й ±а и неизвестна р (доверит. вер-сть). Об измеряемой вел-не известно только, что её знач-

Х

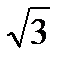е наверняка лежит в опр-ной области и что каждое значение между границами этой области с одинаковой вероятностью может приниматься в расчёт. u(x_i) = а/ , где а – половина интервала неточности измерений

Х

Треугольное распределение – знач-я возле ср. знач-я более вероятны, чем у границ; оценка получена в форме max значений диапазона (±а), опис-го симметричным распределением вероятностей, u(x_i) = а/ 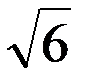, исп-ся, когда рассч-тся неопр- сть мерной посуды

Норм. распр-ние: оценка получена из повторных наблюдений случ. изменяющегося процесса; неопр-ть даётся в форме 95%-го или др. интервала доверия Q без указания вида распр-ния:u(x_i) = а/2, р = 0,95 или u(x_i) = а/3, р = 0,99

Этот закон используется когда известна а и известно р (вероятность, при которой этот интервал был рассчитан)

3) Анализ корреляций Корреляция – зав-сть между вх-ми величинами х_i. Имеется ввиду не только математич. зависимость, но и логическая зависимость. Например, если х₁ и х₂ измеряют одним и тем же средством измерения, то между ними есть связь.Если установлена связь между входными величинами, то силу связи оценивают коэф-том корреляции r(x₁, x₂) и коэф-ты корреляции используют в формулах при дальнейших расчетах, однако чаще всего в методиках указывают, что корреляционная связь отсутствует.

4) Расчет оценки выходной величины. Оценка выходной величины – это и есть результат измерения; оценку рассчитывают подставляя в

формулу связи оценки входных величин х_i вместо входных величин Х_i.

5) Расчет стандартной неопр-сти выходной величины. Станд неопр-сть вых-й вел-ны (сумм. станд. неопр-сть) рассч-ся суммир-ем станд. неопр-стей вх-х вел-н с учетом КЧ: u_c(y) = , где с_i – коэф-ент чувствительности (КЧ), который показывает как изменяется выходная величина у с изменением входной величины х_i, с_i = - частн. произв-ная выходной величины у от входной величины х_i

Иногда КЧ принимаются = 1, когда много влияющих факторов, которые не входят в формулу и нельзя вычислить их КЧ.

Если с_i = 1, формула упрощается u_c(y) = . Эту формулу можно использовать если все x_i выражены в одних единицах, т.е. когда эта модель – сумма или разность: у = х₁ ± х₂. Если x_i выражены в разных единицах (модель – частное или произведение, н-р, у = х₁·х₂/х₃), тогда суммировать можно только относительные неопр-сти:

6) Расчет расширенной неопр-сти. Расширенную неопр-сть U получают путем умножения стандартной неопр-сти выходной величины u_c(y) на коэф-ент охвата к: U = ku_c(y). К = 2 при р = 0,95 и к = 3 при р = 0,99

При выборе коэф-та охвата след. учитывать требуемый ур-нь достоверности; инф-цию о предполагаемом распределении; информацию о количестве наблюдений, использованных для оценки случайных эффектов.

7) Представление результата: 1) у (ед-ц) при станд. неопределенности u_c(y)(единиц) – если мерой неопр-сти явл-ся сумм. станд. неопр-ть;

2) (у±U) ед. измерения р = 0,95, где цифра следующая за ± расширенная неопр-сть, рассчитанная при доверительной вероятности 0,95 – если мерой неопр-ти явл. расшир. неопр-ть.

 

 

Эмпирический метод оценивания неопределенности. Использование оценок правильности и прецизионности, полученных в одной лаборатории, в разных лабораториях, по результатам контроля компетентности лаборатории для оценки неопределенности.

Основной принцип эмпирического подхода закл-ся в определении оценок неопр-сти из оценок прецизионности и правильности. Оценки

прецизионности и смещения могут быть получены:

1) по рез-там внутрилаб-ного контроля;

2) по результатам межлабораторного контроля (аккредитованные лаборатории участвуют в сличительных испытаниях, результаты которых могут быть использованы для оценки неопр-сти);

3) по результатам контрольной компитентности лабораторий (проводит орган по аккредитации либо другая вышестоящая организация);

4) по результатам оценки точности методики выполнения измерений (данные по точности есть в МВИ)

Эмпирический метод позволяет оценить неопр-сть измерительного метода, а не неопр-сть конкретного результата.

Оценки прециз-сти и смещения охватывают все эффекты случ. и систематические, влияющие на результаты измерений. Лаборатории, получив оценку неопр-сти по этому методу, могут использовать ее для оценки точности результатов измерений, полученных по конкретной МВИ.

По рез-там контроля в одной лаб-рии можно оценить лаб-ную неопр-сть конкр-го метода. Неопр-сть измер-й оцен-тся как корень из суммы квадратов станд. отклонения S, хар-щего прецизионность измер-й, и оценки b, рассч-й для смещения: , S – СКО промежуточной прецизионности или СКО повторяемости. Лучше использовать СКО промежуточной прецизионности, т.к. оно учитывает влияние большого числа факторов. b = 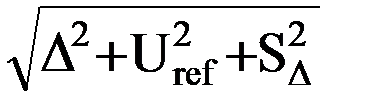, где D - смещение, D = ; и U_ref – неопр-сть эталонного материала, используемого для оценки смещения; S_D - СКО результатов оценки смещения.

Результаты межлаб-ных иссл-ний могут быть использованы для оценки неопр-сти метода в целом. Для оценки неопр-сти используется СКО воспроизводимости.

Если лаборатория участвует в сличительном испытании по проверке ее технической компетентности, то она может использовать данные, полученные в результате такой проверки при оценки неопр-сти. Такая проверка чаще всего связана с измерением стандартного образца. По результатам проверки можно рассчитать смещение: D = . Оценку смещения используют для расчета неопр-сти: .

 

 

101. Общие принципы валидации методов. Виды валидации. Методы подлежащие валидации. Классификация методов испытаний.

Виды валидации процесса:

· Перспективная валидация-валидация, выполняемая до начала серийного производства продукции, предназначенной для реализации.

· Сопутствующая - валидация, которая проводится в ходе серийного производства продукции, предназначенной для продажи.

· Ретроспективная валидация - аттестация серийного процесса производства реализуемого продукта, основанная на полученных данных о производстве и контроле серий продукции.

· Повторнаявалидация (ревалидация) - повторение первичной валидации процесса для обеспечения гарантии того, что изменения в процессе (оборудовании), выполненные в соответствии с процедурой контроля изменений, не ухудшают характеристики процесса и качество продукции.