A. Тындекс музыка
Для всех песен, которые помечены как уже скаченные, посчитаем сумму прЕкольностей. Переберём все прочие песни, и попробуем прибавлять их прЕкольность к этой сумме.
Будем обновлять ответ, если
а) никакого ответа у нас ещё нет
б) у нового ответа прЕкольность ближе к требуемой
в) у нового ответа прЕкольность так же близка к требуемой, что и у текущего, но при этом она больше
B. Сравнить деревья
Вариант 1: делаем строковое представление каждого дерева, и сравниваем эти представления. Делать их можно так:
Строковое представление вершины = буква в ней + символ ‘{‘ + строковые представления её дочерних вершин, упорядоченные лексикографически + символ ‘}’
Важно как-то помечать переходы на уровень ниже или выше (например, символами ‘{‘ и ‘}’), иначе разные деревья могут дать одинаковые строковые представления.
Вариант 2: делаем то же самое, но не со строками, а с хэшами
C. Рефакторинг
Считаем два массива (назовём их a и b). Далее, найдём все позиции i, на которых a[i] не равно b[i]. Их количество – количество благоприятных исходов (когда Витя находит ошибку). Разделив его на общее количество возможных исходов (то есть на количество элементов одного массива) получим искомую вероятность.
D. Топология
Вариант 1: серия DFS (или BFS), объединённых внешней очередью. Запускаем обход для какой-то области, все клетки другого цвета, которых она касается, заносим в очередь (и помечаем, что родительской для них является текущая область). Затем достаём клетки из очереди и повторяем для них то же самое. Параллельно с этим формируем дерево.
Вариант 2: алгоритм 0-1-BFS. Клетки того же цвета добавляем в начало дека, другого цвета – в конец.
E. Добрый гном
Изначально нам известно, что клад лежит в клетке с номером от 1 до 
. Если гном уже сообщал нам какую-то информацию, то у диапазона допустимых значений будут другие границы.
Пусть мы выбрали какое-то значение из этого диапазона и выкопали яму в клетку с соответствующим номером. Если мы при этом угадали клетку с кладом, то на этом его поиск будет завершён, но нас интересует худший случай (в котором мы совершим максимальное количество действий). Пусть после выкапывания мы получаем информацию от гнома о том, меньше номер клетки с кладом, чем номер текущей клетки, или больше.
(на рисунке L и R – текущие границы диапазона возможных значений для номера клетки с кладом)
После ответа гнома, у нас остаётся только правая либо левая часть диапазона. В худшем случае мы остаёмся с больший из двух диапазонов. Чтобы больший из двух диапазонов был как можно меньше, они должны быть равны между собой (или отличаться всего на 1).
Этого мы добьёмся, если номер клетки для раскопок всегда будем выбирать как середину текущего диапазона. Продолжать мы это можем столько раз, сколько можно поделить на 2. Этот процесс можно проэмулировать, либо можно написать формулу с двоичным логарифмом.
F. Злой гном
Будем решать задачу методом динамического программирования.
Рассмотрим произвольный момент времени: Паша находится в какой-то позиции и имеет какие-то знания о том, выше какой и ниже какой высоты клад не может находиться, при этом в текущей позиции он яму уже копал. Его состояние в этом случае мы можем описать следующими параметрами:
Координата x
Координата y
L – минимальное значение номера клетки с кладом
R - максимальное значение номера клетки с кладом
Если теперь мы переберём все клетки от L до R, для каждой клетки C найдём ответ на вопрос «за какое минимальное количество единиц времени мы точно найдём ответ, если следующей выкопанной клеткой будет C», а потом из всех этих ответов выберем минимум, то мы сможем дать ответ на тот же вопрос и для текущей клетки.
Координаты x и y меняют значение от 1 до 20, L и R – от 1 до 400. То есть, всего нужно рассмотреть 20*20*400*400 = 64000000 состояний. Чтобы дважды не рассматривать одно состояние, нам нужно запоминать уже вычисленные значения.
Сократим количество памяти, которое на это потребуется.
Заметим, что после очередного ответа гнома или L = Cur + 1, или R = Cur – 1 (где Cur – значение в клетке x, y, которую мы выкапывали последней). Значит, нам достаточно хранить только одну границу диапазона, а вторая вычисляется по x, y и знанию о том, правую или левую границу мы храним явно.
Тогда состояний будет всего 20*20*400*2
В добавок к этому, нужно учитывать, что изначально мы находимся в клетке (1, 1), но не выкапывали в ней яму (и не обязаны начинать раскопки именно с неё). Это можно обойти, добавив в рекурсивную функцию дополнительный параметр для начальной ситуации. Если мы находимся в ней, то L и R не должны вычисляться исходя из X и Y, а равны 1 и соответственно.
G. Страница "Тренировки"
Первый вариант решения – явно построить дерево и посчитать число вершин в нём. Рёбрами дерева будут являться части пути и короткие названия.
Второй вариант решения – отсортируем все полные названия лексикографически. Каждое новое полное название добавит столько вершин в дерево, сколько новых звеньев на его конце (то есть с момента, когда пути стали различаться в сравнении с предыдущей строкой).
H. Поиск предателя
Рассмотрим сначала несколько частных случаев.
Случай 1.
Пусть у нас есть всего один день, 1024 подозреваемых и 10 задач. Тогда мы без труда найдём предателя следующим образом: каждому подозреваемому сопоставим число от 0 до 1023. В двоичной записи этих чисел как раз 10 бит. Дадим каждому подозреваемому свой, уникальный набор задач (те задачи, чьи биты равны 1 в номере подозреваемого).
По тому, какие задачи были слиты, однозначно восстанавливается номер предателя.
Случай 2
У нас есть 10 задач, но подозреваемых меньше, всего 1000. Максимизируем количество задач, которые не будут скомпрометированы.
1) Заметим, что мы можем никому из подозреваемых не давать номер 1023 (состоящий из 10 единиц в двоичной записи). Тогда никому мы не дадим все 10 задач. Значит, кто бы ни оказался предателем, он сольёт не более 9 задач. Одну задачу мы спасли.
2) Сколько существует номеров, в которых единичных бит ровно 9? Нетрудно посчитать, что их 10 (мы выбираем 1 бит из 10, который будет равен 0). Если мы отнимем от 1024 сначала 1, а потом ещё 10, то всё ещё останется 1013 номеров, чего нам достаточно для 1000 подозреваемых. То есть, мы можем не давать никому номера, требующие выдачи 9 задач одному человеку. Таким образом, кто бы ни слил задачи, мы точно спасём хотя бы 2 из них.
3) Можем ли мы спасти 3 задачи? Для этого нам бы потребовалось из 1013 вариантов вычесть количество чисел, в которых 8 единичных бит из 10. Посчитать их количество можно как 
(или, что то же самое,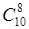 
). Таких чисел
1023 – 45 < 1000, так что оставшихся номеров нам не хватит на всех подозреваемых.
Если дней больше одного, то в первый день мы можем назначит какой-то номер целой группе подозреваемых. Если мы выясним, что именно в ней предатель (если сработает эта комбинация), то на второй день число людей n будет равно числу людей в этой группе, число дней станет меньше на 1, а число ещё не слитых задач будет равно числу нулевых бит в номере группы.
То есть, чем меньше в номере группы единиц, тем больше задач мы сможем использовать для поиска предателя в ней в оставшиеся дни.
Напишем для нахождения ответа рекурсивную функцию SOL (m, k, p) - максимальное количество людей, среди которых мы можем найти предателя за m дней, имея в распоряжении k задач, из которых слитыми окажутся максимум t.
C(k, t) людям мы можем рассказать какие-нибудь t из k задач, и по соответствующей маске определим сразу предателя.
Каждый из С(k, t - 1) наборов по t-1 задач из k мы можем рассказать количеству людей равному SOL(m - 1, k - (t - 1), 1).
И так далее до С(k, 1)
Среди всех SOL (m, k, p) > n выберем минимальное p – это минимизированное количество идей, которые не будут сохранены.
I. Маркерная доска
Построим граф, вершинами которого являются слова. Между вершинами есть ребро тогда, когда слова в них отличаются только в 1 букве. Если мы берём одно слово из какой-то компоненты связности, то сможем получить из него все остальные.
Таким образом, нужно определить число компонент связности такого графа.
J. Марш несогласных
Можем сразу вычислить матожидание ответа, который даёт любой несогласный (среднее арифметическое всех возможных ответов из набора несогласных). Назовём эту величину Xср.
Посчитаем теперь матожидание для каждого района. Если с вероятность p ученик из района является несогласным, то матожидание для ответа ученика из этого района составит
p * Xср + (1 – p) * 4
Зная матожидания для всех районов, получим искомую величину. Для этого просуммируем матожидания для районов, умноженные на число учеников из них, а полученную сумму поделим на общее количество учеников.
Убедитесь в том, что выводите достаточное количество знаков после десятичной точки.
K. Пароль от старого сейфа
Переберём все пароли. Для каждого из них будем проверять, есть ли i-я буква пароля среди букв на цилиндре i. В тех ограничениях, в которых дана задача, делать это можно даже перебирая каждый раз все буквы на цилиндре.
Отобранные таким образом пароли нужно отсортировать в алфавитном порядке.