1.1 Расчет параметров и составление уравнения двигателя постоянного тока (объем - 2 часа).
Цель и задачи занятия:
- изучение принципа действия двигателя постоянного тока;
- получение дифференциальных уравнений описывающих работу двигателя постоянного тока;
- получение передаточной функции двигателя постоянного тока.
Наибольшее использование в системах автоматического управления, работающих на постоянном токе, имеют двигатели с независимым возбуждением. Такие двигатели, управляемые путем изменения напряжения на якоре, позволяют получить широкий диапазон регулирования скорости вращения, благодаря чему широко применяются в качестве исполнительных элементов в регулируемом приводе многих производственных механизмов и в силовых следящих системах.
Принципиальная схема двигателя постоянного тока с независимым возбуждением показана на рисунке 1.
 |
Рассмотрим статический режим работы двигателя. В этом случае без учета реакции якоря для двигателя можно записать:
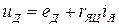, (1.1)
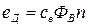, (1.2)
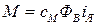, (1.3)
где: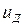 
- напряжение на якоре двигателя [в],
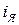- ток якоря [а],
- сопротивление цепи якоря [ом],
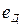- э.д.с. вращения [в],
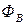- поток возбуждения [вб],
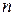- скорость вращения двигателя [об/мин],
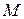- момент, развиваемый двигателем [н·м],
, 
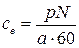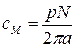- конструктивные постоянные,
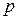- число пар полюсов,
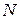- число активных проводников якоря, равное удвоенному числу витков обмотки якоря 
,
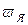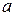- число пар параллельных ветвей обмотки якоря.
В установившемся режиме момент двигателя уравновешивается приведенным к валу статическим моментом сопротивления рабочего механизма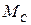 
, то есть в этом случае 
.
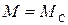Следует обратить внимание на соотношение
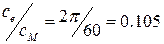, (1.4)
которое может использоваться в расчетах.
Из (1.1) – (1.3) получаем уравнения механической характеристики двигателя в виде
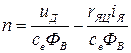, (1.5)
или
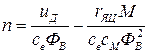. (1.6)
В формулах (1.5) и (1.6) в правой части первый член соответствует скорости вращения при идеальном холостом ходе (
, 
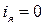), а второй – снижению скорости вращения двигателя под нагрузкой. Механическая характеристика двигателя пр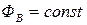и 
, и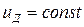 
выражается уравнением прямой (рисунок 2, прямая 1). При увеличении сопротивления якорной цепи жесткость механической характеристики двигателя ухудшается (прямая 2).
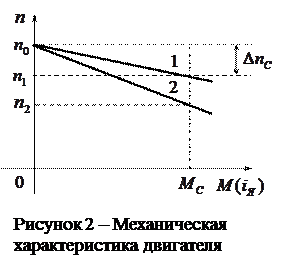Конструктивные постоянные двигателя можно определить по его номинальным данным. Из уравнения (1.5), можно определить
. (1.7)
Для определения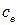 
можно воспользоваться также формулой
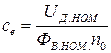, (1.8)
где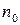 
- скорость вращения при идеальном холостом ходе, определенная по механической характеристике при 
.
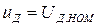Из уравнения (1.3) можно определить значение
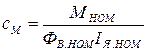. (1.9)
Момент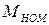 
можно определить по механической характеристике при 
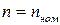или по формуле
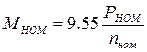, (1.10)
где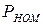 
- номинальная мощность на валу двигателя, [вт].
Формулы (1.7) – (1.9) используются для приближенного вычисления постоянных 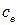и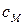 
, так как номинальные данные для двигателя представляют собой усредненные величины.
Рассмотрим регулирование скорости вращения двигателя путем изменения напряжения на якоре. Механические характеристики двигателя, построенные по уравнению (1.6) при разных напряжениях на якоре, изображены на рисунке 3. При уменьшении напряжения механическая характеристика смещается параллельно вниз пропорционально величине напряжения.
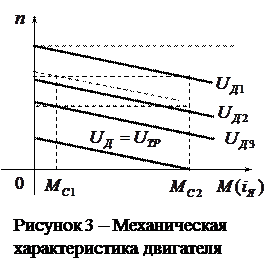Статические характеристики позволяют определить диапазон изменения напряжения на якоре двигателя, требуемый для поддержания заданной скорости вращения при заданных пределах изменения статического момента 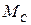. Соответствующие значения тока якоря можно найти используя соотношение (1.3). График, приведенный на рисунке 3, позволяет также определить зону нечувствительности двигателя, определяемую напряжением трогания (
).
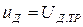Это напряжение соответствует началу вращения двигателя и зависит от момента сопротивления на валу 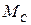. Величина 
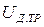может быть найдена также из (1.3) или (1.4) пр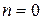и 
и .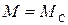
Составим уравнение динамики двигателя в отклонениях при 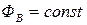, не учитывая для упрощения реакцию якоря. За входную величину примем напряжение на якоре, а за выходную – скорость вращения. Рассмотрим случай, когда момент сопротивления на валу двигателя не зависит от скорости вращения. При этом введем следующие обозначения
, 
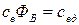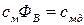. (1.11)
Для цепи якоря, учитывая, что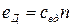 
, при нулевых начальных условиях запишем
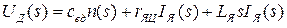. (1.12)
Заменив в формуле для динамического момента двигателя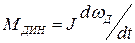 
угловую скорость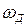 
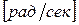на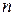 
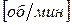, получим в изображениях уравнение равновесия моментов:
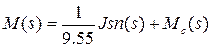, (1.13)
где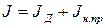 
- момент инерции на валу двигателя 
,
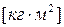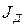- момент инерции якоря двигателя,
- момент инерции нагрузки приведенный к валу двигателя,
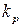- коэффициент передачи редуктора соединяющего вал двигателя с нагрузкой.
Используя зависимость
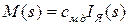. (1.14)
После совместного решения (12) – (14) запишем уравнение двигателя:
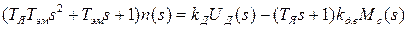, (1.15)
где 
- постоянная времени цепи якоря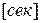 
,
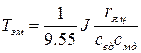- электромеханическая постоянная времени ,
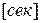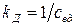- коэффициент передачи двигателя по управляющему воздействию 
,
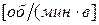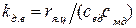- коэффициент передачи двигателя по возмущающему воздействию 
.
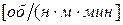Вычислить индуктивность якоря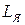 
сложно, поэтому на практике ее определяют экспериментально. Приближенно величина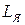 
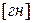
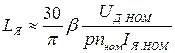, (1.16)
где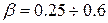 
- коэффициент нижнее значение которого принимается для компенсированных машин, верхнее – для некомпенсированных.
Для определения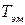 
имеется также соотношение
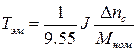, 1. (17)
где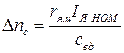 
- падение скорости двигателя в номинальном режиме.
Анализируя уравнение (1.15), можно установить, что при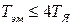 
двигатель обладает колебательными свойствами, которые являются нежелательными. Поэтому при конструировании двигателей стремятся выполнить соотношение 
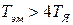. В этом случае уравнение динамики двигателя можно записать в виде
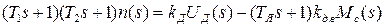, (1.18)
где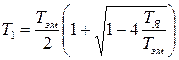 
, 
.
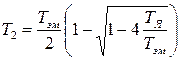В случае когда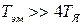 
, пренебрегая величиной 
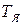, уравнение двигателя можно свести к приближенному уравнению первого порядка.
Передаточные функции двигателя по управляющему и возмущающему воздействиям равны соответственно:
, 
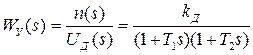. (1.19)
Часто за выходную величину двигателя принимается угол поворота вала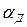 
, обычно измеряемый в радианах. При этом, учитывая, что 
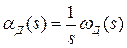, а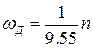 
, получаем вместо (19) другие передаточные функции двигателя
,
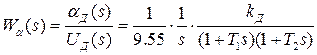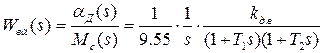. (1.20)
Контрольные вопросы.
1) Какими уравнениями описывается статический режим работы двигателя постоянного тока?
2) Какой вид имеет механическая характеристика двигателя постоянного тока?
3) Какой вид имеют передаточные функции двигателя постоянного тока по управляющему и возмущающемуся воздействию?
1.2 Расчет параметров и составление уравнения двухфазного асинхронного двигателя (объем - 2 часа).
Цель и задачи занятия:
- изучение принципа действия двухфазного асинхронного двигателя;
- получение дифференциальных уравнений описывающих работу двухфазного асинхронного двигателя;
- получение передаточной функции двухфазного асинхронного двигателя.
Двухфазные асинхронные двигатели широко используются в автоматических системах. Наибольшее применение как исполнительные элементы они находят в маломощных следящих системах. Практическое достоинство этих двигателей заключается в том, что они не имеют коллектора и поэтому обладают высокой надежностью.
В основном выпускаются двухфазные асинхронные двигатели двух типов: с полым немагнитным ротором из материала с хорошей электропроводимостью (обычно из алюминия) и ферромагнитным ротором, имеющим короткозамкнутую обмотку в виде беличьей клетки. Имея меньший к.п.д., двигатели первого типа отличаются малой инерцией ротора и лучшими регулировочными свойствами. Мощность указанных типов двигателей не превышает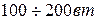 
.
Принципиальная схема двухфазного асинхронного двигателя показана на рисунке 4. Обмотка возбуждения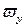 
и обмотка возбуждения 
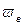расположены перпендикулярно друг к другу. Необходимый фазовый сдвиг между напряжениями на обмотках, равный 
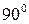, обеспечивается с помощью конденсатора 
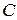, включенного в цепь обмотки возбуждения. Могут применяться и другие схемы включения обмоток.
Механические характеристики асинхронного двигателя нелинейные и зависят не только от собственных параметров, но и от параметров выходного каскада усилителя и схемы включения обмоток. Поэтому механические характеристики, используемые в расчетах, должны соответствовать реальным условиям работы двигателя.
Как правило, такие характеристики определяются экспериментально. Обычно в справочниках приводятся технические данные двигателей для показанной на рисунке 4 схемы соединения обмоток при управлении от источника с большой мощностью и малым внутренним сопротивлением.
С помощью механичес-ких характеристик 
(рисунок 5а) можно найти
управляющее напряжение при заданном статическом моменте сопротивления на валу и напряжение трогания двигателя.
Составим линейное уравнение динамики двигателя в отклонениях, проведя линеаризацию его механических характеристик. За входную величину примем напряжение на управляющей обмотке, а за выходную – угол поворота вала, полагая момент сопротивления не зависящим от скорости вращения, что соответствует большинству применений двухфазных асинхронных двигателей.
Механические характеристики двигателя следует линеаризовать в точке или области рабочего режима путем построения касательных к действительным характеристикам. Если по форме механические характеристики близки к линейным, то их можно заменить приближенными линейными характеристиками в виде параллельных прямых (рисунок 5б). Наклон данных прямых равен усредненному наклону прямых, соединяющих при заданных управляющих напряжениях точки пусковых моментов и холостого хода.
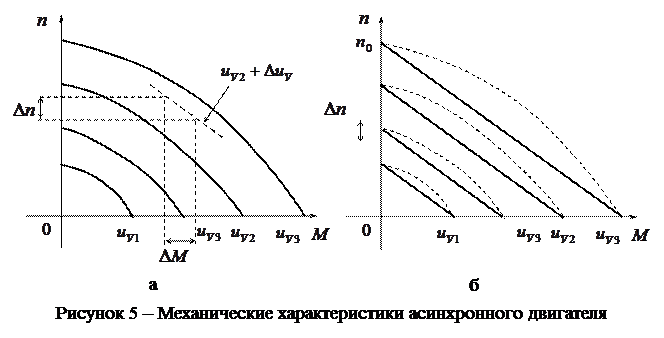
Из дальнейшего рассмотрения исключим инерционность по цепи управления двигателя, так как эта величина практически очень мала. Проведя аналогию с двигателем постоянного тока при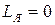 
, на основании уравнения (1.6) для асинхронного двигателя при постоянной амплитуде напряжения возбуждения и малых отклонениях переменных можно записать:
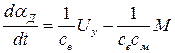, (1.21)
где: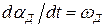 
- скорость вращения двигателя [рад/сек],
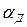- угол поворота двигателя [рад],
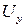- действующее значение напряжения на обмотке управления [в],
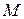- момент двигателя 
,
, 
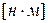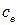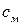- постоянные двигателя, определяемые в области рабочего режима 
, 
.
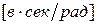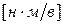При этом уравнение равновесия моментов имеет вид
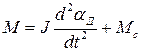. (1.22)
Решив совместно (1.21), (1.22) и перейдя к изображениям, получим уравнение двухфазного асинхронного двигателя
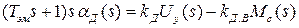, (1.23)
где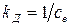 
, 
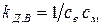- коэффициенты передачи двигателя соответственно по управляющему и возмущающему воздействиям,
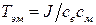- электромеханическая постоянная времени [сек],
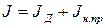- момент инерции на валу двигателя ,
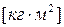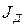- момент инерции ротора двигателя .
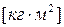Постоянные 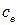, 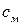могут быть найдены на основании (1.21) по механическим характеристикам. При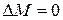 
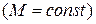получаем
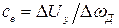. (1.24)
Принимая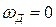 
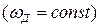, находим
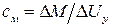. (1.25)
В случае приведения механических характеристик двигателя (рисунок 5б)
, 
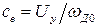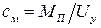, (1.26)
где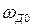 
, 
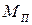- скорость при холостом ходе и пусковой момент двигателя при напряжении .
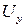При отсутствии механических характеристик постоянные двигателя можно определить приближенно по его номинальным данным. Если механическую характеристику двигателя на рабочем участке от номинальной скорости вращения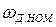 
до 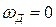при номинальном напряжении управления 
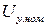считать линейной, то
, 
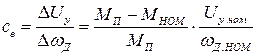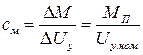, (1.27)
где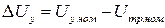 
, 
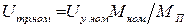- напряжение трогания двигателя при номинальном моменте.
В последнем случае коэффициенты уравнения двигателя запишутся как
, 
, 
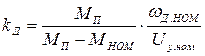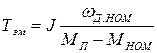. (1.28)
Так как в справочных сведениях скорость вращения двигателя задается в оборотах в минуту, следует учитывать соотношение
.
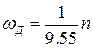Передаточные функции двигателя на основании (1.23) имеют вид:
, 
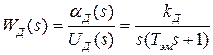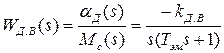. (1.29)
Контрольные вопросы.
1) Какими уравнениями описывается статический режим работы двухфазного асинхронного двигателя?
2) Какой вид имеет механическая характеристика двухфазного асинхронного двигателя?
3) Какой вид имеют передаточные функции двухфазного асинхронного двигателя по управляющему и возмущающемуся воздействию?
1.3 Составление передаточных функций динамических звеньев (объем - 1 час).
Цель и задачи занятия:
- переход к операторной записи дифференциального уравнения;
- получение передаточных функций динамических звеньев;
- рассмотрение различных примеров получения передаточных функции динамических звеньев.
Для расчета систем автоматического регулирования они обычно разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления, но описываемое определенным дифференциальным уравнением. В соответствии с этим классификация звеньев производится именно по виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, гидравлические, электрические, пневматические и т.д.).
Предположим, что динамическое звено описывается однородным линейным дифференциальным уравнением первого порядка, представленным в стандартной форме:
.
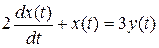Учитывая, что оператор преобразования Лапласа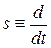 
, а переменные равны, соответственно
, 
, 
,
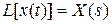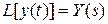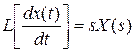получим операторную запись данного дифференциального уравнения:
.
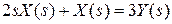Далее можно получить выражение передаточной функции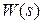 
динамического звена описываемого заданным дифференциальным уравнением. Для этого необходимо определить отношение вида 
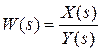. Тогда получим:
.
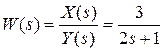Пусть динамическое звено описывается однородным линейным дифференциальным уравнением второго порядка, представленным в стандартной форме:
.
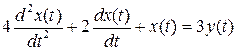Учитывая, что оператор преобразования Лапласа 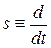, а переменные равны, соответственно
, , , 
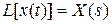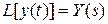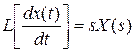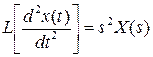
получим операторную запись данного дифференциального уравнения:
.
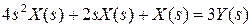Далее можно получить выражение передаточной функции 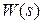динамического звена описываемого заданным дифференциальным уравнением. Для этого необходимо определить отношение вида 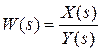. Тогда получим:
.
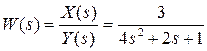Рассмотрим пример, когда динамическое звено описывается неоднородным линейным дифференциальным уравнением второго порядка, представленным в стандартной форме:
.
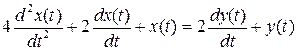Учитывая, что оператор преобразования Лапласа 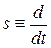, а переменные равны, соответственно
, , , 
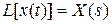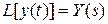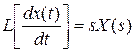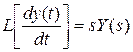
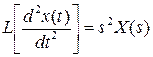
получим операторную запись данного дифференциального уравнения:
.
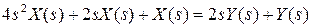Далее можно получить выражение передаточной функции 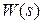динамического звена описываемого заданным дифференциальным уравнением. Для этого необходимо определить отношение вида 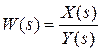. Тогда получим:
.
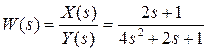Контрольные вопросы.
1) Как осуществляется переход к операторной форме записи дифференциального уравнения?
2) Приведите основные формулы преобразования Лапласа?
1.4 Частотная передаточная функция и частотные характеристики динамических звеньев (объем - 2 часа).
Цель и задачи занятия:
- переход от передаточной функции к частотной передаточной функции;
- вещественная и мнимая части частотной передаточной функции;
- амплитудная фазовая частотная характеристика динамического звена;
- амплитудная частотная характеристика динамического звена;
- фазовая частотная характеристика динамического звена.
Для получения частотной передаточной функции можно произвести формальную замену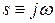 
. Это связано с тем, что формулы, описывающие передаточную функцию 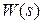, и частотную передаточную функцию 
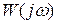совпадают. Рассмотрим реализацию этой процедуры на простом примере, пусть передаточная функция динамического звена, называемого апериодическим звеном первого порядка имеет следующий вид:
.
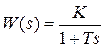Получим выражение для частотной передаточной функции
.
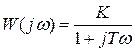Представим частотную передаточную функцию в ви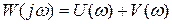де 
, где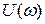 
- действительная часть, а 
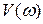- мнимая часть частотной передаточной функции. Для получения вещественной и мнимой частей необходимо избавиться от мнимой составляющей в знаменателе частотной передаточной функции. Для этого умножим числитель и знаменатель частотной передаточной функции на комплексно сопряженный сомножитель знаменателя частотной передаточной функции. В итоге мы избавимся от комплексной составляющей в знаменателе. Рассмотрим вышеприведенный пример:
,
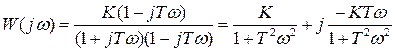тогда
, 
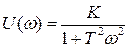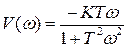. (1.30)
Тогда, частотную передаточную функцию можно представить в виде графика на комплексной плоскости. Для этого необходимо найти изменение годографа вектора частотной передаточной функции при изменении частоты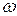 
от 0 до 
.
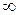Полученная характеристика называется амплитудно-фазовой частотной характеристикой (АФХ) динамического звена. Для рассматриваемого примера эта характеристика представлена на рисунке 6.
Как видно из рисунка данная характеристика представляет собой полуокружность радиуса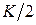 
имеющего центр в точке с координатами 
и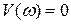 
. При угловой частоте 
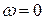АФХ начинается с точки с координатам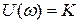и 
и 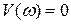. При угловой частоте 
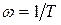АФХ проходит через точку с координатами и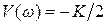 
.
Рассмотрим точку АФХ при угловой частоте равной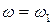 
. В этой точке модуль и аргумент частотной передаточной функции равны соответственно
, 
.
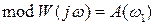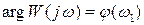Полученная функция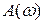 
определяет амплитудную частотную характеристику динамического звена. Её можно определить, зная вещественную и мнимую части частотной передаточной функции (1.30), тогда
.
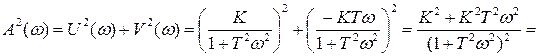
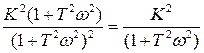отсюда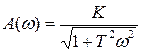 
.
Вид амплитудной частотной характеристики апериодического звена первого порядка приведен на рисунке 7.
Как видно из рисунка 7 при угловой частоте равной 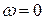значение 
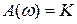, далее с увеличением угловой частоты характеристика уменьшается, и стремиться к нулю. При частоте 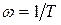значение амплитудной частотной характеристики равно 
.
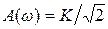Далее рассмотрим значение аргумента частотной передаточной функции.
Значение аргумента частотной передаточной функции представляет собой следующее выражение:
.
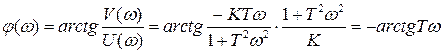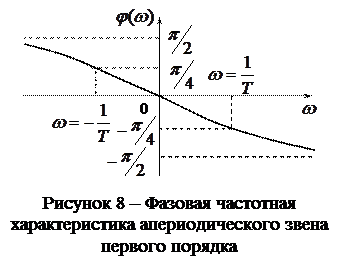Полученную функцию называют фазовой частотной характеристикой апериодического звена первого порядка. Она имеет вид представленный на рисунке 8. Как видно из рисунка 8 фазовая частотная характеристика проходит через точку сдвига фазового угла 
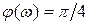или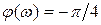 
при значении угловой частоты равно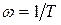й или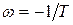 
соответственно.
Далее рассмотрим апериодическое звено второго порядка, передаточная функция которого имеет:
.
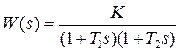Получим выражение для частотной передаточной функции
.
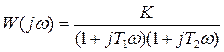Определим действительную 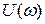и мнимую 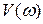составляющие частотной передаточной функции:
,
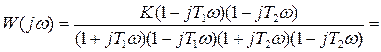
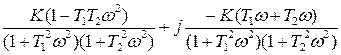тогда
, 
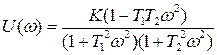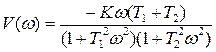. (1.31)
Тогда, АФХ апериодического звена второго порядка имеет вид представленный на рисунке 9.
Амплитудную частотную характеристику 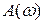апериодического звена второго порядка определим на основе вещественной и мнимой частей частотной передаточной функции (1.31):
= 
=
= 
=
= 
,
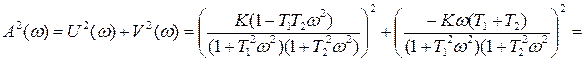
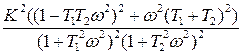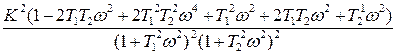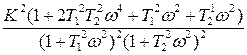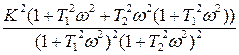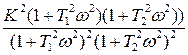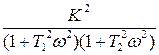отсюда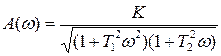 
.
Вид амплитудной частотной характеристики апериодического звена второго порядка приведен на рисунке 10.
Определим выражение фазовой частотной характеристикой апериодического звена второго порядка:
=
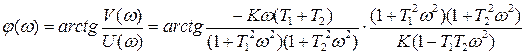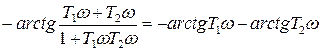
Она имеет вид представленный на рисунке 11.
Рассмотрим колебательное звено, передаточная функция которого имеет следующий вид:
.
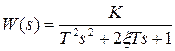Частотная передаточная функция этого звена равна
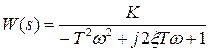
Определим действительную 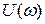и мнимую 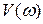составляющие частотной передаточной функции:
,
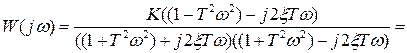
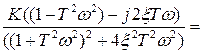
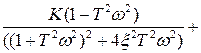
тогда
, 
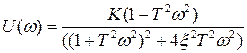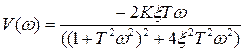. (1.32)
Тогда, АФХ колебательного звена имеет вид представленный на рисунке 12.
Амплитудную частотную характеристику 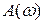колебательного звена определим на основе вещественной и мнимой частей частотной передаточной функции (1.32):
= 
= 
,
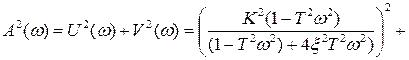
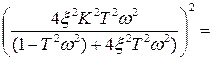
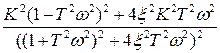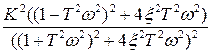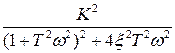Отсюда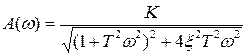 
.
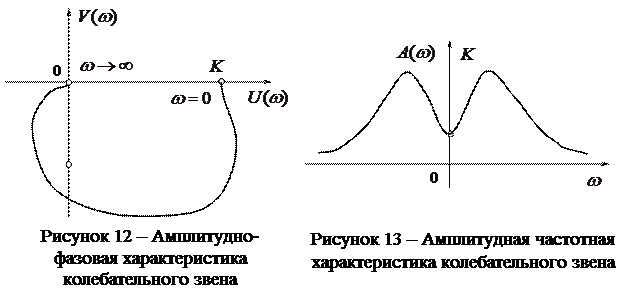Вид амплитудной частотной характеристики колебательного звена приведен на рисунке 13.
Определим выражение фазовой частотной характеристикой колебательного звена:
=
.
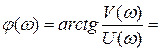
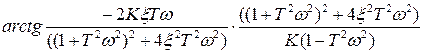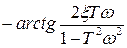Она имеет вид представленный на рисунке 14.
Контрольные вопросы.
1) Как строится АФХ динамического звена?
2) Как строится АЧХ динамического звена?
3) Как строится ФЧХ динамического звена?
1.5 Логарифмические частотные характеристики динамических звеньев (объем - 1 час).
Цель и задачи занятия:
- построение логарифмической амплитудной частотной характеристики;
- построение логарифмической фазовой частотной характеристики;
Главным достоинством логарифмических амплитудных частотных характеристик (ЛАЧХ) динамических звеньев является возможность построения их во многих случаях практически без вычислительных работ. В инженерных расчетах строят на одном графике друг под другом асимптотическую ЛАЧХ и логарифмическую фазовую частотную характеристику (ЛФЧХ).
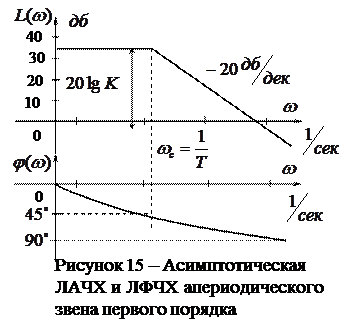Рассмотрим в качестве примера построение асимптотических ЛАЧХ и ЛФЧХ апериодического звена первого порядка (рисунок 15), передаточная функция, которой имеет следующий вид:
.
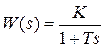Для построения асимпто-тической ЛАЧХ апериодического звена первого порядка необходимо определить значение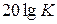 
. Эту величину отложим вдоль оси
кординат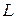 
в децибелах.
Далее определяется значение частоты среза по формуле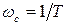 
. Эту величину откладывают по оси абсцисс 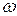в логарифмическом масштабе. Далее проводят прямую линию до частоты среза, после нее
ЛАЧХ имеет наклон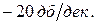 
(рисунок 15). График ЛФЧХ строится как и ранее только частота откладывается в логарифмическом масштабе.
Рассмотрим построение асимптотической ЛАЧХ и ЛФЧХ апериодического звена второго порядка (рисунок 16), передаточная функция, которой имеет следующий вид:
.
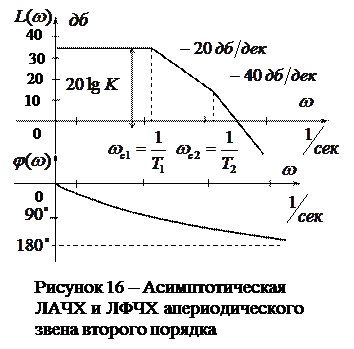
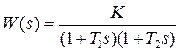Для построения асимптотичес-кой ЛАЧХ апериодического звена второго порядка также необходимо определить значе-ние 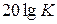. Эту величину отложим вдоль оси ординат 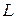в децибелах. Далее определяется значение двух частот среза по формуле 
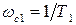и 
. Эти величины откладывают по оси абсцисс 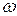в логариф-мическом масштабе. Далее проводят прямую линию до первой частоты среза, после нее проводится линия с наклоном
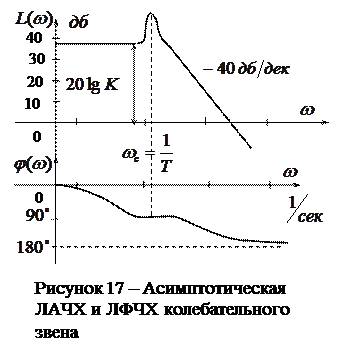
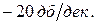до второй частоты среза. После этой частоты среза проводится линия с наклоном 
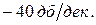(Рисунок 16). График ЛФЧХ строится как и ранее только частота откладывается в логарифмическом масштабе.
Рассмотрим построение асимптотической ЛАЧХ и ЛФЧХ колебательного звена (рисунок 17) передаточная функция, которой имеет следующий вид:
.
|
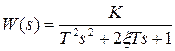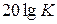. Эту величину отложим вдоль оси ординат 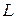в децибелах.
Далее определяется значение частоты среза по формуле 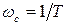. В точке частоты среза ЛАЧХ имеет пик зависящий от величины 
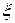. После пика проводят линию с наклоном