Схема поперечного сечения бруса показана на рисунке 5. Сечение является сложным, так как состоит из трех простых сечений (элементов). Первый и третий элементы составного сечения – неравнополочные уголки с размерами 50´32´4 мм, второй элемент – прямоугольник с размерами 160´20 мм.
1, 3 – уголок 50´32´4 мм; 2 – прямоугольник 160´20 мм
Рисунок 5 – Схема поперечного сечения бруса
При определении геометрических характеристик поперечных сечений прокатных профилей будем использовать ГОСТ 8239-89 (Двутавры стальные горячекатаные), ГОСТ 8240-89 (Швеллеры стальные горячекатаные), ГОСТ 8509-93 (Уголки стальные горячекатаные равнополочные), ГОСТ 8510-86 (Уголки стальные горячекатаные неравнополочные). Геометрические характеристики сечений в виде простых геометрических фигур (прямоугольник, круг, кольцо, треугольник) находятся с помощью формул.
Рекомендуется все расчеты выполнять в сантиметрах, а окончательные результаты вычислений перевести в метры.
Вычертим сечение бруса на листе формата А4 в масштабе 1:1 и покажем основные размеры (рисунок 6).
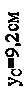
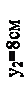
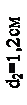
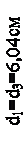
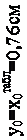
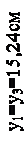
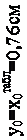
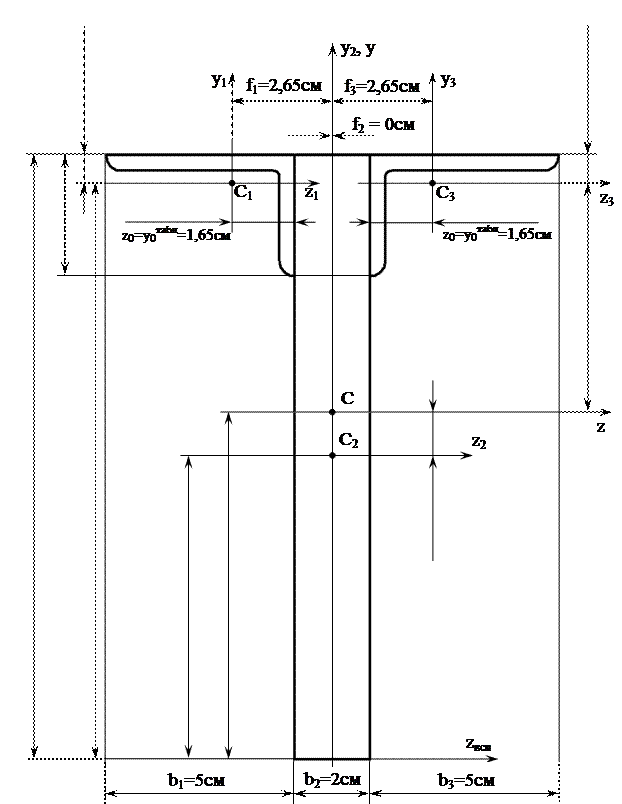
Рисунок 6 – Чертеж составного сечения бруса
Покажем на чертеже положение центров тяжестей простых сечений. Центр тяжести прямоугольника находится на пересечении осей симметрии – горизонтальной Z2 и вертикальной У2. По ГОСТ 8510-86 определим, что расстояние от большей полки до центральной оси (обозначим горизонтальные оси уголков Z1 и Z3), параллельной полке уголка, составляет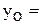 
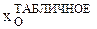=0,76 см. Расстояние от меньшей полки уголка до центральной оси (обозначим вертикальные оси уголков У1 и У3), параллельной полке уголка, составляет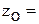 
=1,65 см.
Проведем горизонтальные оси Z1, Z2 и Z3 и вертикальные оси У1, У2 и У3. Пересечение осей Z1 и У1, Z2 и У2, Z3 и У3 обозначим С1, С2 и С3 соответственно. С1, С2 и С3 – центры тяжести простых сечений.
|
|
Важным для решения практических задач является следующее замечание. Если сечение имеет ось симметрии, то центр тяжести сечения обязательно лежит на этой оси. Кроме того, ось симметрии всегда является одной из двух главных осей инерции сечения. Вторая главная ось перпендикулярна первой и проходит через центр тяжести сечения.
Составное сечение (рисунок 6) имеет вертикальную ось симметрии У, которая совпадает с осью У2 прямоугольника. Следовательно, центр тяжести сечения лежит на оси У, а ось У является одной из двух главных осей инерции всего сечения. Чтобы найти положение другой главной оси Z, нужно определить место центра тяжести составного сечения на оси У.
Для этого зададим вспомогательную ось ZВСП. Вспомогательную ось рекомендуется совмещать с самой нижней из осей Z1, Z2 или Z3 или проводить по нижней границе (точке) сечения параллельно осям Z1, Z2, Z3. Совместим ось ZВСП с нижней границей составного сечения.
Расстояние от вспомогательной оси ZВСП до центра тяжести составного сечения по высоте определяется формулой:
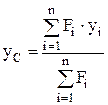, (4)
где n – число элементов составного сечения;
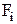– площадь i-го элемента составного сечения, см2;
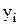– расстояния от вспомогательной оси до центра тяжести i-го элемента
составного сечения, см.
По ГОСТ 8510-86 найдем площади уголков:
.
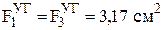Вычислим площадь прямоугольника:
.
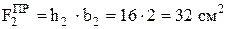Определим расстояния от вспомогательной оси до центра тяжести каждого простого сечения (рисунок 6):
|
|
;
.
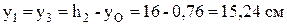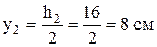Тогда:
.
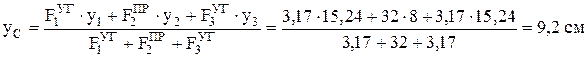На оси У на расстоянии 9,2 см вверх от оси ZВСП отметим точку С – центр тяжести составного сечения. Через точку С перпендикулярно оси У проведем ось Z – вторую главную ось инерции этого сечения.
Главные моменты инерции составного сечения можно вычислить по формулам:
; 
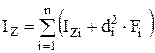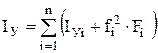, (5)
где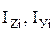 
– моменты инерции i-го сечения относительно собственных цен-
тральных осей Zi и Уi, см4;
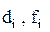– расстояния от главных осей инерции Z и У составного сечения до
осей Zi и Уi, см.
По ГОСТ 8510-86 найдем моменты инерции уголков:
;
.
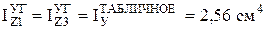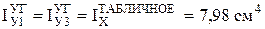Вычислим моменты инерции прямоугольника:
;
.
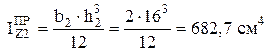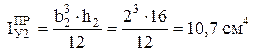По чертежу составного сечения (рисунок 6) определим:
;
;
;
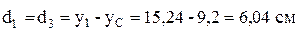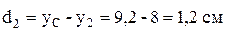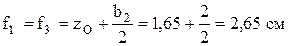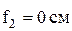, так как оси У и У2 совпадают.
Вычислим моменты инерции составного сечения относительно главных осей Z и У:
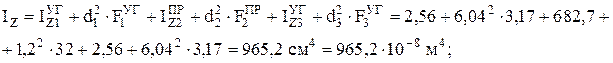
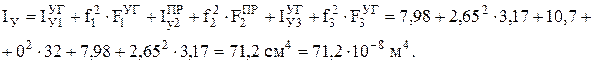
Умение определять геометрические характеристики сложных поперечных сечений брусьев является важной частью практических навыков решения задач, так как все виды расчетов в сопротивлении материалов (расчеты на прочность, жесткость, устойчивость) производятся относительно главных осей инерции. В расчетные формулы входят главные моменты инерции или другие геометрические характеристики сечений, производные от них.