Задание 4
Расчет плоской рамы методом конечных элементов
Задание:
Определить внутренние силовые факторы в элементах и перемещения узлов плоской рамы в случае статического приложения сил и при заданном гармоническом воздействии.
Методические указания и пример расчета
Формирование матриц жесткости и масс в глобальной системе координат для рамы
Узловые перемещения рамного конечного элемента в локальной системе координат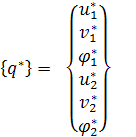 
выражаются через глобальные узловые обобщенны перемещения 
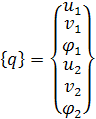и углы α и β рис.1 в виде
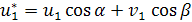
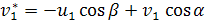
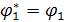
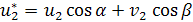
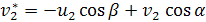
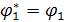
Рис. 1. Преобразование на плоскости узловых перемещений рамного конечного элемента
В матричной форме это преобразование запишем так
где
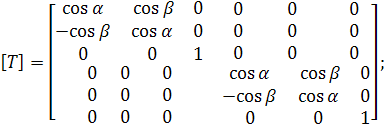(2)
Направляющие косинусы локальной оси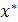 
определяются глобальными координатами узлов
(3)
(4)
где
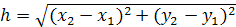(5)
длина элемента.
Матрица жесткости конечного элемента в глобальной системе координат преобразуется с учетом выражения (1) и зависимости для потенциальной энергии элемента, которая не зависит от выбора системы отсчета:
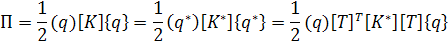
тогда
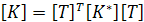(6)
Аналогично преобразуется и матрица масс конечного элемента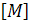 
, на основании того, что кинетическая энергия элемента не зависит от направления осей координат, по аналогии с потенциальной энергией получим:
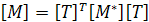(7)
Узловые силы и моменты, приложены к узлам рамы, которые задаются в глобальной системе координат, в преобразованиях не нуждаются.
Силы, заданные в локальной системе отсчета для каждого элемента должны быть приведены к глобальной системе отсчета. Распределенные нагрузки приведенные к узловым силам в локальной системе координат совершают возможную работу на глобальных возможных перемещениях
|
|
,
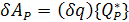где узловые силы в локальной системе отсчета равны
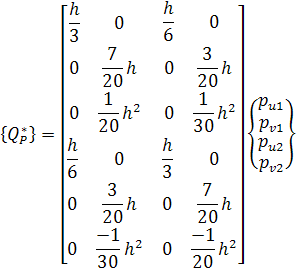
Выразим глобальные перемещения через локальные по уравнениям (1):
,
учитывая
,
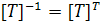
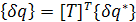или
,
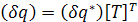тогда
,
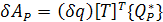Коэффициенты в выражении возможной работы при вариациях обобщенных координат 
есть вклад в обобщенные силы от распределенных внешних нагрузок
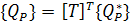(8)
Добавляя в выражение (8) вклад сил заданных в глобальной системе отсчета и объединяя уравнения равновесия для всей совокупности конечных элементов, получим уравнения равновесия системы при статической задаче:
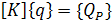(9)
И уравнения динамического равновесия для движения всей конструкции:
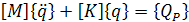(10)
Рассмотрим, как формируется матрица жесткости и уравнения равновесия для механической системы, содержащей рамные конечные элементы (рис. 2), к которой приложены распределенные силы интенсивности p=40 Н/м, сосредоточенные сила F=700 Н и момент M=200 Н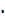 
м (в статике и в динамике при частоте гармонического воздействия всех сил в одной фазе 
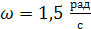). Известны размеры 
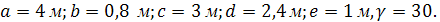Жесткость стержней на растяжение-сжатие составляет EF= 
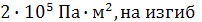EI=4000 
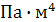. Удельная масса стержней рамы m=100 кг/м.
Без учета закрепления узлов необходимо ввести 24 обобщенных перемещений (по три на каждый из 8 узлов). Матрица жесткости для такой системы будет иметь размер 24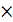 
24, а матрица каждого элемента, приведенная к глобальной системе координат, имеет размер 
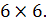Таким образом, конечные элементы, узлы которых совпадают должны вносить общий суммарный вклад в соответствующие элементы матрицы жесткости, причем шарнирно-соединенные элементы получают в точке соединения разные глобальные номера узлов. Это обусловлено тем, что углы поворота таких узлов разные.
|
|
Рис. 2 Рама с номерами узлов: 1...8 и номерами стержней 1...5 (в окружностях)
Рис. 3 Нумерация глобальных обобщенных координат для трех первых элементов с указанием в скобках номеров внутренней нумерации
В качестве исходных данных для формирования матрицы жесткости потребуется координатная матрица для узлов и топологическая матрица для конечных элементов. Координатная матрица – это таблица, которая содержит информацию о номере узла и его координатах, а также о способе его закрепления и приложенных сосредоточенных силовых воздействиях. В соответствии с количеством узлов выбирается число обобщенных перемещений. Для конструкции рисунка 2 с учетом размеров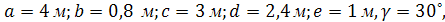 
координатная матрица имеет вид
Таблица 1. Координатная матрица.
| № узла | Координаты | Сосредоточенные силы | Закрепления по | |||||
| x | y |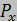 
| 
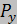
| M | x | y | φ | |
| -1 | -1 | -1 | ||||||
| 
| |||||||
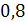
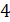
| 3,8 | 
| 
| ||||||
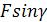
| 3,8 | ||||||||
| 3,8 | ||||||||
| 3,8 | -1 | -1 | -1 | |||||
| 6,2 | M | |||||||
| 7,2 | -1 | -1 |
В последних трех столбцах 0 – соответствует свободному перемещению узла в данном направлении, а (-1) - закрепленному, в соответствии с направлением оси, целые положительные числа указывают на номер узла, у которого данное перемещение должно быть одинаковым с текущим узлом.
Топологическая матрица содержит информацию об элементах конструкции и представляет собой таблицу, столбцы которой соответствуют локальным номерам узлов начала и конца элемента, а строки номеру элемента. Внутренние ячейки таблицы содержат глобальные номера узлов, соответствующие каждому элементу, кроме этой информации в каждую строку добавляем характеристики распределенных сил и прочностные и массовые свойства элементов. Для конструкции рисунка 2 топологическая матрица примет вид
|
|
Таблица 2. Топологическая матрица.
| № элемента | Узлы | Значения px в узлах,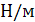 
| Значения py в узлах,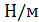 
| EF,
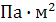
| EI,
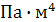
| m, кг/м | |||
| нач. | 2 кон. | нач. | кон. | 1 нач. | кон. | ||||
| |||||||||
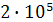
| -40 | -40 |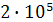
| |||||||
|
| |||||||||
|
| |||||||||
|
|
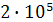
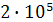
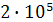
По координатной и топологической матрицам формируется матрица индексов – это таблица, строки которой соответствуют номерам элементов, а столбцы локальным номерам обобщенных перемещений. Внутренние ячейки содержат глобальные номера обобщенных перемещений:
Таблица 3. Матрица индексов.
| № элемента | Номера перемещений Начальный узел Конечный узел | |||||
| 1 (u1) | 2 (v1) | 3 (φ1) | 4 (u2) | 5 (v2) | 6 (φ2) | |
По топологической и координатной матрицам вычисляются также направляющие косинусы и длины элементов (формулы (3),(4),(5)) и матрицы жесткости каждого элемента в отдельности (1). В строках матрицы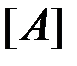 
указаны глобальные номера узловых перемещений конечных элементов в порядке следования соответствующих им локальных номеров. Число строк в матрице 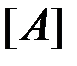равно числу конечных элементов f1.m:
for (int i = 0; i < f1.m; i++)
{
// Формирование матрицы индексов
A[i, 0] = i + 1;
A[i, 1] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3 - 2;
A[i, 2] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3-1;
A[i, 3] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3;
A[i, 4] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3-2;
A[i, 5] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3-1;
A[i, 6] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3;
}
Затем с помощью матрицы индексов суммируем элементы отдельных матриц элементов в общую матрицу жесткости системы. Ниже приведен фрагмент программы на языке С# реализующий процесс сборки:
for (int ii = 0; ii < f1.m; ii++)
{
...//Формирование матрц элемента
for (int i = 1; i <= 6; i++)
{
int ig = A[ii, i];
for (int j = 1; j <= 6; j++)
{
int jg = A[ii, j];
K[ig - 1, jg - 1] = K[ig - 1, jg - 1] + Ke1[i - 1, j - 1];
M[ig - 1, jg - 1] = M[ig - 1, jg - 1] + Me1[i - 1, j - 1];
}
}
}
Обозначения в программе:
· ii – номер текущего конечного элемента;
· f1.m – число конечных элементов;
· A – матрица индексов перемещений;
· i, j – локальные индексы узловых перемещений конечного элемента;
· ig, jg – соответствующие им глобальные индексы, выбираемые из матрицы A;
· K –матрица жесткости конструкции;
· Ke1 – матрица жесткости текущего конечного элемента с номером ii, вычисленная в глобальной системе координат.
Аналогично формируется матрица масс M конструкции при решении динамической задачи.
Учет граничных условий
Граничные условия делятся на естественные и главные. В качестве естественных граничных условий выступают внешние силы, которые входят в правую часть уравнений равновесия. Для формирования вектора нагрузки организуем цикл с обходом узлов рамы в координатной матрице и добавим в его ячейки силы из четвертого, пятого и шестого столбцов таблицы в соответствии с номерами обобщенных перемещений. Кроме того в столбец обобщенных сил необходимо добавить вклад от распределенных сил, указанных в топологической матрице для каждого элемента, приведенный по выражению (8) к глобальным осям координат.
Главные граничные условия – это условия закрепления конструкции. При наложении условий закрепления, то есть уменьшении количества степеней свободы системы, уравнения не вычеркивают, а заменяют фиктивными для сохранения нумерации в матрицах. Один из способов состоит в обнулении всех элементов строки, кроме диагонального для данного элемента и обнуление соответствующего элемента столбца нагрузки.
Если перемещения в закрепленных узлах не равны нулю, то их действительные значения, умноженные на диагональный элемент матрицы жесткости, помещают в соответствующую строку вектора нагрузки.
Когда в матрице узлов в столбцах 7,8,9 стоят (-1) – это означает закрепление данного узла по соответствующему направлению: x,y,φ.
for (int i = 0; i < f1.n; i++)
{
//Наложение главных граничных условий для неподвижных опор
if (Convert.ToInt32(f1.MatrCoor[i, 6]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i, j] = 0;
}
K1[3 * i, 3 * i] = K[3 * i, 3 * i];
P[3 * i] = 0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 7]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i + 1, j] = 0;
}
K1[3 * i + 1, 3 * i + 1] = K[3 * i + 1, 3 * i + 1];
P[3 * i + 1] = 0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 8]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i + 2, j] = 0;
}
K1[3 * i + 2, 3 * i + 2] = K[3 * i + 2, 3 * i + 2];
P[3 * i + 2] = 0;
}
}
Случай, когда в столбцах 7,8,9 стоят нули, означает отсутствие закрепления.
Если в ячейках этих столбцов стоят положительные целые числа, то это означает, что данное перемещение равно перемещению узла по соответствующему направлению, с номером, указанным в ячейке.
Такое явление возникает при наличии в системе внутренних шарниров, муфт и других видов связей. При этом внешние силы, приложенные в шарнире во всех узлах, прикладывают к одному из узлов, примыкающему к шарниру. Коэффициенты, стоящие вне главной диагонали в матрицы жесткости для других узлов примыкающих к шарниру обнуляются, а на место элемента, соответствующего первому узлу, помещается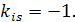 
Диагональный коэффициент этой же строки матрицы приравнивается единице 
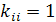, так, что для обусловленных перемещений уравнения принимают вид
,
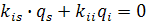где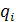 
- перемещение второго (третьего и т. д.) узла в шарнире, 
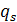- перемещение первого узла в шарнире, уравнение которого не обнулялось и к которому отнесены все узловые силы, приложенные в шарнире по данному направлению:
for (int i = 0; i < f1.n; i++)
{
//Наложение главных граничных условий для подвижных соединений
if (Convert.ToInt32(f1.MatrCoor[i, 6]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 6]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh, j] = K1[3 * sh, j] + K1[3 * i, j];
K1[3 * i, j] = 0;
}
P[3 * sh] = P[3 * i] + P[3 * sh];
P[3 * i] = 0;
K1[3 * i, 3 * sh] = -1.0;
K1[3 * i, 3 * i] = 1.0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 7]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 7]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh + 1, j] = K1[3 * sh + 1, j] + K1[3 * i + 1, j];
K1[3 * i + 1, j] = 0;
}
P[3 * sh + 1] = P[3 * i + 1] + P[3 * sh + 1];
P[3 * i + 1] = 0;
K1[3 * i + 1, 3 * sh + 1] = -1.0;
K1[3 * i + 1, 3 * i + 1] = 1.0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 8]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 8]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh + 2, j] = K1[3 * sh + 2, j] + K1[3 * i + 2, j];
K1[3 * i + 2, j] = 0;
}
P[3 * sh + 2] = P[3 * i + 2] + P[3 * sh + 2];
P[3 * i + 2] = 0;
K1[3 * i + 2, 3 * sh + 2] = -1.0;
K1[3 * i + 2, 3 * i + 2] = 1.0;
}
}