Таким образом, уравнения равновесия для фермы примут вид
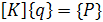 . (11)
. (11)
Решение системы уравнений (8) сводится к вычислению вектора-столбца неизвестных перемещений 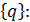
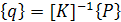 . (12)
. (12)
Существуют стандартные программы решения системы линейных алгебраических уравнений методом Гаусса без нахождения обратной матрицы к матрице жесткости (SIMQ “Fortrun”).
После решения уравнений (11) и нахождения узловых обобщенных перемещений по выражению (1) определяются узловые перемещения в локальной системе координат для каждого элемента
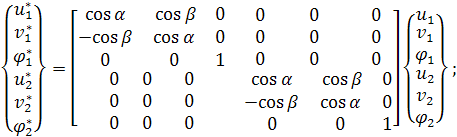 (13)
(13)
По узловым обобщенным перемещениям можно найти величину относительной деформации, соответствующие нормальной силе 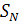 , поперечной силе
, поперечной силе 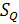 и изгибающему моменту
и изгибающему моменту 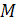 (рис. 4):
(рис. 4):
Рис. 4. Вычисление относительных деформаций
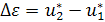 ;
;
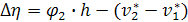 ;
;
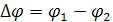 ;
;
Данные соотношения позволяют найти внутренние силы в первом узле:
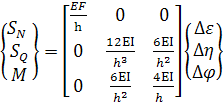 , (14)
, (14)
где квадратная матрица есть часть локальной матрицы жесткости (левый верхний угол). Столбцы этой матрицы показывают внутренние силы в первом узле при единичном смещении в соответствующем направлении данного узла и жестком закреплении второго узла. Значения двух силовых факторов постоянны по длине элемента  ,
, 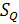 и равны в первом и втором узлах элемента.
и равны в первом и втором узлах элемента.
В соответствии с правилом знаков, по которому при положительном изгибающем моменте растянуты нижние волокна
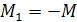
Изгибающий момент во втором узле определим из соотношения:
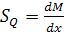 ,
,
и линейного характера изменения изгибающего момент в пределах элемента:
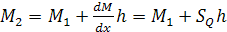 (15)
(15)
На эпюре моментов ось направлена вниз относительно оси элемента 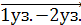
Для решения динамической задачи формируется система уравнений вида:
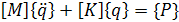 , (16)
, (16)
в которой глобальная матрица масс 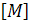 формируется аналогично матрице жесткости путем сложения матриц масс элементов.
формируется аналогично матрице жесткости путем сложения матриц масс элементов.
Поиск частного решения уравнения (16), при гармоническом внешнем воздействии 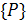 , сводится к заданию выражения для обобщенных перемещений
, сводится к заданию выражения для обобщенных перемещений 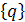 в виде функций, подобных правой части уравнения.
в виде функций, подобных правой части уравнения.
Пусть внешние силы изменяются по закону:
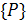 =
= 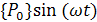 , (17)
, (17)
тогда произвольное частное решение уравнения (16), соответствующее установившемуся режиму представим в виде
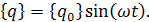 (18)
(18)
Вторая производная от выражения (18) равна
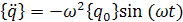
Подставляя выражение (15) в уравнение (13), получим
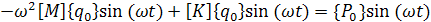
Приравнивая коэффициенты в левой и правой части при 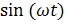 , приходим к линейной системе алгебраических уравнений:
, приходим к линейной системе алгебраических уравнений:
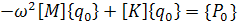 ,
,
вынесем за скобки неизвестные амплитудные значения
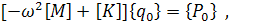 (19)
(19)
Обозначим
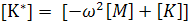 ,
,
тогда уравнение (19) становится аналогичным (11)
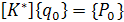 (20)
(20)
В матрице 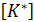 и столбце
и столбце 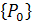 необходимо преобразовать строки, соответствующие перемещениям на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (20) решается с помощью программы, реализующей метод Гаусса, и находятся амплитуды вынужденных колебаний
необходимо преобразовать строки, соответствующие перемещениям на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (20) решается с помощью программы, реализующей метод Гаусса, и находятся амплитуды вынужденных колебаний  в решении (18) для установившегося режима.
в решении (18) для установившегося режима.
По амплитудам  , аналогично статическому решению вычисляют амплитуды внутренних силовых факторов по соотношениям (13), (14), (15).
, аналогично статическому решению вычисляют амплитуды внутренних силовых факторов по соотношениям (13), (14), (15).
Текст клиентского кода программы и результаты расчетов в статике:
Форма1
System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.IO;
using System.Drawing.Drawing2D;
namespace Рама
{
public partial class Form1: Form
{
public Form2 f2;
Form3 f3;
List<string> list_st = new List<string>();
string st;
string[] St;
public bool dinamika = false;
public Double[,] MatrCoor, MatrTop;
public double[] q;
public int i = 0, j = 0, n = 0, m = 0;
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
Close();
}
private void сохранитьВФайлToolStripMenuItem_Click(object sender, EventArgs e)
{
//Сохранение в файл координатной матрицы
n = 0;
for (i = 0; i < dataGridView1.RowCount - 1; i++) n++;
MatrCoor = new double[n, 9];
for (i = 0; i < n; i++)
{
for (j = 0; j < 9; j++)
MatrCoor[i, j] = Convert.ToDouble(dataGridView1.Rows[i].Cells[j].Value);
}
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FileStream FS = saveFileDialog1.OpenFile() as FileStream;
StreamWriter SR = new StreamWriter(FS);
//dataGridView1.Rows.Add();
for (i = 0; i < n; i++)
{
st = null;
for (j = 0; j < 9; j++)
{
st = st + MatrCoor[i, j].ToString() + " ";
}
SR.WriteLine(st);
}
SR.Close();
FS.Close();
}
}
private void считатьИзФайлаToolStripMenuItem_Click(object sender, EventArgs e)
{
// Считывание из файла координатной матрицы
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
FileStream FSR = openFileDialog1.OpenFile() as FileStream;
StreamReader SRR = new StreamReader(FSR);
dataGridView1.Rows.Clear();
list_st.Clear();
while (SRR.Peek() > 0)
{
list_st.Add(SRR.ReadLine());
//dataGridView1
dataGridView1.Rows.Add();
}
St = list_st.ToArray();
n = St.Length;
MatrCoor = new double[n, 9];
// MatrCoor = new Double[n, 7];
for (i = 0; i < n; i++)
{
St[i] = St[i].Replace(".", ",");;
//Разбиение строки St на подстроки aa
string[] aa = St[i].Split(" \t".ToCharArray(), StringSplitOptions.RemoveEmptyEntries);
for (j = 0; j < aa.Length; j++)
{
//Заполнение матрицы и таблицы
MatrCoor[i, j] = Convert.ToDouble(aa[j]);
dataGridView1.Rows[i].Cells[j].Value = MatrCoor[i, j];
}
}
SRR.Close();
FSR.Close();
}
}
private void сохранитьВФайлToolStripMenuItem1_Click(object sender, EventArgs e)
{
// Сохранение в файл топологической матрицы
m = 0;
for (i = 0; i < dataGridView2.RowCount - 1; i++) m++;
MatrTop = new double[m, 11];
for (i = 0; i < m; i++)
{
for (j = 0; j < 10; j++)
MatrTop[i, j] = Convert.ToDouble(dataGridView2.Rows[i].Cells[j].Value);
}
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FileStream FS = saveFileDialog1.OpenFile() as FileStream;
StreamWriter SR = new StreamWriter(FS);
//dataGridView1.Rows.Add();
for (i = 0; i < m; i++)
{
st = null;
for (j = 0; j < 10; j++)
{
st = st + MatrTop[i, j].ToString() + " ";
}
SR.WriteLine(st);
}
SR.Close();
FS.Close();
}
}
private void считатьИзФайлаToolStripMenuItem1_Click(object sender, EventArgs e)
{
// Считывание из файла топологической матрицы
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
FileStream FSR = openFileDialog1.OpenFile() as FileStream;
StreamReader SRR = new StreamReader(FSR);
dataGridView2.Rows.Clear();
list_st.Clear();
while (SRR.Peek() > 0)
{
list_st.Add(SRR.ReadLine());
//dataGridView1
dataGridView2.Rows.Add();
}
St = list_st.ToArray();
m = St.Length;
MatrTop = new double[m, 10];
// MatrTop = new Double[m, 10];
for (i = 0; i < m; i++)
{
St[i] = St[i].Replace(".", ",");;
//Разбиение строки St на подстроки aa
string[] aa = St[i].Split(" \t".ToCharArray(), StringSplitOptions.RemoveEmptyEntries);
for (j = 0; j < aa.Length; j++)
{
//Заполнение матрицы и таблицы
MatrTop[i, j] = Convert.ToDouble(aa[j]);
dataGridView2.Rows[i].Cells[j].Value = MatrTop[i, j];
}
}
SRR.Close();
FSR.Close();
}
}
private void button2_Click(object sender, EventArgs e)
{
//Построение
double[] x, y;
Double My = 0, MaxY = 0, Mx = 0, MaxX = 0;
int[] yint, xint;
Bitmap myBmp;
x = new double[n];
y = new double[n];
for (i = 0; i < n; i++)
{
x[i] = MatrCoor[i, 1];
y[i] = MatrCoor[i, 2];
}
if (x == null || y == null) return;
MaxY = 0.001;
MaxX = 0.001;
for (i = 0; i < n; i++)
{
if (System.Math.Abs(y[i]) > MaxY)
{
MaxY = System.Math.Abs(y[i]);;
}
if (System.Math.Abs(x[i]) > MaxX)
{
MaxX = System.Math.Abs(x[i]);
}
}
if (MaxY >= MaxX)
MaxX = MaxY;
else
MaxY = MaxX;
My = (pictureBox1.Height) / 1.2 / MaxY;
Mx = (pictureBox1.Width) / 1.2 / MaxX;
yint = new int[n];
xint = new int[n];
for (int i = 0; i < n; i++)
{
yint[i] = Convert.ToInt32(pictureBox1.Height / 1.1) - Convert.ToInt32(y[i] * My);
xint[i] = Convert.ToInt32(pictureBox1.Width / 10) + Convert.ToInt32(x[i] * Mx);
}
myBmp = new Bitmap(pictureBox1.Width, pictureBox1.Height);
Graphics gr1 = Graphics.FromImage(myBmp);
Pen P1 = new Pen(Color.Red, 2);
gr1.DrawRectangle(P1, 1, 1, pictureBox1.Width - 2, pictureBox1.Height - 2);
Pen P2 = new Pen(Color.Green, 2);
Pen P5 = new Pen(Color.Green, 12);
Brush B2 = new SolidBrush(Color.Azure);
Brush B3 = new SolidBrush(Color.Brown);
int[] Zakx = new int[n];
int[] Zaky = new int[n];
int[] ZakFi = new int[n];
for (i = 0; i < n; i++)
{
Zakx[i] = Convert.ToInt32(MatrCoor[i, 6]);
Zaky[i] = Convert.ToInt32(MatrCoor[i, 7]);
ZakFi[i] = Convert.ToInt32(MatrCoor[i, 8]);
}
Pen P3 = new Pen(Color.Brown, 4);
Pen P6 = new Pen(Color.Aqua, 18);
for (i = 0; i < m; i++)
{
//Построение распределенной нагрузки
if ((MatrTop[i, 3]!= 0) || (MatrTop[i, 4]!= 0) || (MatrTop[i, 5]!= 0) || (MatrTop[i, 6]!= 0))
{
gr1.DrawLine(P6, xint[(int)MatrTop[i, 1] - 1], yint[(int)MatrTop[i, 1] - 1], xint[(int)MatrTop[i, 2] - 1], yint[(int)MatrTop[i, 2] - 1]);
}
//Построение линий конечных элементов
gr1.DrawLine(P3, xint[(int)MatrTop[i, 1] - 1], yint[(int)MatrTop[i, 1] - 1], xint[(int)MatrTop[i, 2] - 1], yint[(int)MatrTop[i, 2] - 1]);
}
//Нанесение прямоугольников на расположение узлов
for (i = 0; i < n; i++)
{
gr1.FillRectangle(B3, xint[i] - 4, yint[i] - 4, 8,8);
gr1.DrawRectangle(P2, xint[i] - 4, yint[i] - 4, 8, 8);
}
// Линии шириной 12 п. в точках закрепления
for (i = 0; i < n; i++)
{
if (Zakx[i] < 0 || Zaky[i] < 0)
{
gr1.DrawLine(P5, xint[i] - 24, yint[i] + 10, xint[i] + 24, yint[i] + 10);
}
//Нанесение окружностей на расположение шарниров
if ((Zakx[i]!= 0 || Zaky[i]!= 0) & (ZakFi[i] == 0))
{
gr1.FillEllipse(B2, xint[i] - 6, yint[i] - 6, 12, 12);
gr1.DrawEllipse(P2, xint[i] - 6, yint[i] - 6, 12, 12);
}
}
double Mp = 0, MaxP = 0.001, P = 0;
double[] Px = new double[n];
double[] Py = new double[n];
double[] PM = new double[n];
int[] intPx = new int[n];
int[] intPy = new int[n];
Pen P4 = new Pen(Color.Indigo, 6);
// Стиль пера с наконечниками
P4.SetLineCap(LineCap.Flat, LineCap.ArrowAnchor, DashCap.Flat);
//Изображение сил и моментов
for (i = 0; i < n; i++)
{
Px[i] = MatrCoor[i, 3];
Py[i] = MatrCoor[i, 4];
PM[i] = MatrCoor[i, 5];
P = Math.Sqrt(Px[i] * Px[i] + Py[i] * Py[i]);
if (MaxP <= P)
MaxP = P;
}
Mp = pictureBox1.Width / 8 / MaxP;
for (i = 0; i < n; i++)
{
intPy[i] = Convert.ToInt32(Py[i] * Mp);
intPx[i] = Convert.ToInt32(Px[i] * Mp);
}
for (i = 0; i < n; i++)
{
if (intPx[i]!= 0 || intPy[i]!= 0)
{
gr1.DrawLine(P4, xint[i], yint[i], xint[i] + intPx[i], yint[i] - intPy[i]);
}
if (PM[i]>0)
{
gr1.DrawArc(P4, xint[i]-20, yint[i]-20, 40,40,0,-150);
}
if (PM[i] < 0)
{
gr1.DrawArc(P4, xint[i] - 20, yint[i] - 20, 40, 40, 0, 150);
}
}
//---------------------------------------------------------------------------------------
//Построение второго слоя после вычисления перемещений
double[] x1 = new double[n];
double[] y1 = new double[n];
double Md = 1;
// Условие продолжения построений
if (q!= null)
{
Md = Convert.ToDouble(textBox2.Text);
for (i = 0; i < 3 * n; i++)
{
if (i % 3 == 0)
{
x1[i / 3] = x[i / 3] + q[i] * Md;
y1[i / 3] = y[i / 3] + q[i+1] * Md;
}
}
int[] yint1 = new int[n];
int[] xint1 = new int[n];
for (int i = 0; i < n; i++)
{
yint1[i] = Convert.ToInt32(pictureBox1.Height / 1.1) - Convert.ToInt32(y1[i] * My);
xint1[i] = Convert.ToInt32(pictureBox1.Width / 10) + Convert.ToInt32(x1[i] * Mx);
}
Pen P11 = new Pen(Color.Aqua, 1);
gr1.DrawRectangle(P11, 1, 1, pictureBox1.Width - 2, pictureBox1.Height - 2);
Pen P12 = new Pen(Color.Green, 1);
Pen P15 = new Pen(Color.Green, 2);
Brush B12 = new SolidBrush(Color.Azure);
Pen P26 = new Pen(Color.Aqua, 9);
Pen P13 = new Pen(Color.Red, 2);
for (i = 0; i < m; i++)
{
if ((MatrTop[i, 3]!= 0) || (MatrTop[i, 4]!= 0) || (MatrTop[i, 5]!= 0) || (MatrTop[i, 6]!= 0))
{
gr1.DrawLine(P26, xint1[(int)MatrTop[i, 1] - 1], yint1[(int)MatrTop[i, 1] - 1], xint1[(int)MatrTop[i, 2] - 1], yint1[(int)MatrTop[i, 2] - 1]);
}
gr1.DrawLine(P13, xint1[(int)MatrTop[i, 1] - 1], yint1[(int)MatrTop[i, 1] - 1], xint1[(int)MatrTop[i, 2] - 1], yint1[(int)MatrTop[i, 2] - 1]);
}
for (i = 0; i < n; i++)
{
// gr1.FillRectangle(B2, xint1[i] - 4, yint1[i] - 4, 8, 8);
gr1.DrawRectangle(P2, xint1[i] - 4, yint1[i] - 4, 8, 8);
}
for (i = 0; i < n; i++)
{
if (Zakx[i] < 0 || Zaky[i] < 0)
{
gr1.DrawLine(P5, xint[i] - 24, yint[i] + 10, xint[i] + 24, yint[i] + 10);
}
if ((Zakx[i]!= 0 || Zaky[i]!= 0) & (ZakFi[i] == 0))
{
gr1.FillEllipse(B2, xint1[i] - 6, yint1[i] - 6, 12, 12);
gr1.DrawEllipse(P2, xint1[i] - 6, yint1[i] - 6, 12, 12);
}
}
Pen P14 = new Pen(Color.Blue, 3);
// Стиль пера с наконечниками
P14.SetLineCap(LineCap.Flat, LineCap.ArrowAnchor, DashCap.Flat);
for (i = 0; i < n; i++)
{
intPy[i] = Convert.ToInt32(Py[i] * Mp);
intPx[i] = Convert.ToInt32(Px[i] * Mp);
}
Pen P24 = new Pen(Color.Blue, 1);
P24.SetLineCap(LineCap.Flat, LineCap.ArrowAnchor, DashCap.Flat);
for (i = 0; i < n; i++)
{
if (intPx[i]!= 0 || intPy[i]!= 0)
{
gr1.DrawLine(P14, xint1[i], yint1[i], xint1[i] + intPx[i], yint1[i] - intPy[i]);
}
if (PM[i] > 0)
{
gr1.DrawArc(P24, xint1[i] - 20, yint1[i] - 20, 40, 40, 0, -150);
}
if (PM[i] < 0)
{
gr1.DrawArc(P24, xint1[i] - 20, yint1[i] - 20, 40, 40, 0, 150);
}
}
}
pictureBox1.Image = myBmp;
}
private void матрицаЖесткостиToolStripMenuItem_Click(object sender, EventArgs e)
{
// Запуск статических вычислений
// Вычисление
// Создание формы 2
f2 = new Form2(this);
f2.Show();
}
private void продольнаяСилаToolStripMenuItem_Click(object sender, EventArgs e)
{
f3 = new Form3(this);
f3.Show();
}
private void матрицаЖесткостиToolStripMenuItem1_Click(object sender, EventArgs e)
{
dinamika = true;
матрицаЖесткостиToolStripMenuItem_Click(sender, e);
dinamika = false;
}
private void амплитудыМоментовToolStripMenuItem_Click(object sender, EventArgs e)
{
продольнаяСилаToolStripMenuItem_Click(sender, e);
}
}
}
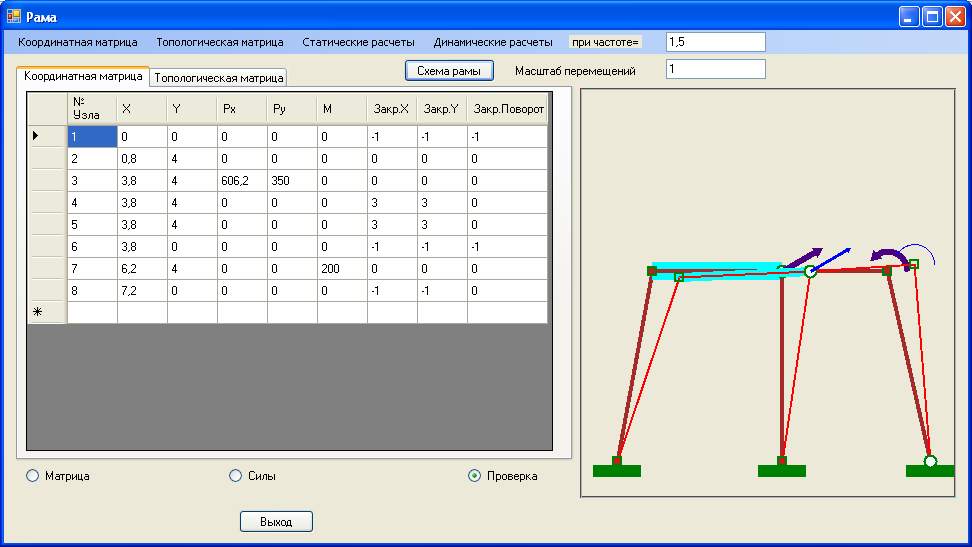
Рис. 5. Главная форма проекта – форма 1
Форма2
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
namespace Рама
{
public partial class Form2: Form
{
//Вычисление матрицы жесткости
Form1 f1;
public double[,] K, K1, Ke, Ke1, T, Tt, TtK, M, Me, Me1, TtM, pxy, Qpxy;
public double[] P, P1;
public int[,] A;
public double w = 0;
public Form2(Form1 f1)
{
InitializeComponent();
this.f1 = f1;
Demo();
}
void Demo()
{
if (f1.n > 0)
{
for (int i = 0; i < 3 * f1.n; i++)
{ // Добавление колонки
DataGridViewTextBoxColumn titleColumn1 = new DataGridViewTextBoxColumn();
titleColumn1.HeaderText = "Titlt" + (i + 1).ToString();
//Выравнивание ширины колонки в соответствии с заданным стилем - AllCells
titleColumn1.AutoSizeMode = DataGridViewAutoSizeColumnMode.AllCells;
dataGridView1.Columns.Add(titleColumn1);
dataGridView1.Rows.Add();
}
}
P = new double[3 * f1.n];
P1 = new double[3 * f1.n];
K = new double[3 * f1.n, 3 * f1.n];
M = new double[3 * f1.n, 3 * f1.n];
K1 = new double[3 * f1.n, 3 * f1.n];
A = new int[f1.m, 7];
pxy = new double[f1.m, 4];
Qpxy = new double[f1.m, 6];
double[,] Ht = new double[6, 4];
double[] Qp = new double[6];
for (int i = 0; i < f1.n * 3; i++)
{
if (i % 3 == 0)
{
P[i] = f1.MatrCoor[i / 3, 3];
P[i + 1] = f1.MatrCoor[i / 3, 4];
P[i + 2] = f1.MatrCoor[i / 3, 5];
}
//dataGridView1.Rows[i].Cells[0].Value = P[i];
}
for (int i = 0; i < f1.m; i++)
{
// Формирование матрицы индексов
A[i, 0] = i + 1;
A[i, 1] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3 - 2;
A[i, 2] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3 - 1;
A[i, 3] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3;
A[i, 4] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3 - 2;
A[i, 5] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3 - 1;
A[i, 6] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3;
pxy[i, 0] = f1.MatrTop[i, 3];
pxy[i, 1] = f1.MatrTop[i, 4];
pxy[i, 2] = f1.MatrTop[i, 5];
pxy[i, 3] = f1.MatrTop[i, 6];
}
//Формирование матрицы жесткости и масс
if (f1.dinamika)
w = Convert.ToDouble(f1.textBox1.Text);
for (int ii = 0; ii < f1.m; ii++)
{
Ke = new double[6, 6];
Ke1 = new double[6, 6];
Me = new double[6, 6];
Me1 = new double[6, 6];
T = new double[6, 6];
Tt = new double[6, 6];
TtK = new double[6, 6];
TtM = new double[6, 6];
double x1 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 1]) - 1, 1];
double y1 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 1]) - 1, 2];
double x2 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 2]) - 1, 1];
double y2 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 2]) - 1, 2];
double h = Math.Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
double cosA = (x2 - x1) / h;
double cosB = (y2 - y1) / h;
double EF = f1.MatrTop[ii, 7];
double EI = f1.MatrTop[ii, 8];
double mm = f1.MatrTop[ii, 9];
//Матрица преобразования координат
T[0, 0] = cosA;
T[0, 1] = cosB;
T[0, 2] = 0;
T[0, 3] = 0;
T[0, 4] = 0;
T[0, 5] = 0;
T[1, 0] = -cosB;
T[1, 1] = cosA;
T[1, 2] = 0;
T[1, 3] = 0;
T[1, 4] = 0;
T[1, 5] = 0;
T[2, 0] = 0;
T[2, 1] = 0;
T[2, 2] = 1;
T[2, 3] = 0;
T[2, 4] = 0;
T[2, 5] = 0;
T[3, 0] = 0;
T[3, 1] = 0;
T[3, 2] = 0;
T[3, 3] = cosA;
T[3, 4] = cosB;
T[3, 5] = 0;
T[4, 0] = 0;
T[4, 1] = 0;
T[4, 2] = 0;
T[4, 3] = -cosB;
T[4, 4] = cosA;
T[4, 5] = 0;
T[5, 0] = 0;
T[5, 1] = 0;
T[5, 2] = 0;
T[5, 3] = 0;
T[5, 4] = 0;
T[5, 5] = 1;
//Локальная матрица жесткости
Ke[0, 0] = EF / h;
Ke[0, 1] = 0;
Ke[0, 2] = 0;
Ke[0, 3] = -EF / h;
Ke[0, 4] = 0;
Ke[0, 5] = 0;
Ke[1, 0] = 0;
Ke[1, 1] = 12 * EI / Math.Pow(h, 3);
Ke[1, 2] = 6 * EI / Math.Pow(h, 2);
Ke[1, 3] = 0;
Ke[1, 4] = -12 * EI / Math.Pow(h, 3);
Ke[1, 5] = 6 * EI / Math.Pow(h, 2);
Ke[2, 0] = 0;
Ke[2, 1] = 6 * EI / Math.Pow(h, 2);
Ke[2, 2] = 4 * EI / Math.Pow(h, 1);
Ke[2, 3] = 0;
Ke[2, 4] = -6 * EI / Math.Pow(h, 2);
Ke[2, 5] = 2 * EI / Math.Pow(h, 1);
Ke[3, 0] = -EF / h;
Ke[3, 1] = 0;
Ke[3, 2] = 0;
Ke[3, 3] = EF / h;
Ke[3, 4] = 0;
Ke[3, 5] = 0;
Ke[4, 0] = 0;
Ke[4, 1] = -12 * EI / Math.Pow(h, 3);
Ke[4, 2] = -6 * EI / Math.Pow(h, 2);
Ke[4, 3] = 0;
Ke[4, 4] = 12 * EI / Math.Pow(h, 3);
Ke[4, 5] = -6 * EI / Math.Pow(h, 2);
Ke[5, 0] = 0;
Ke[5, 1] = 6 * EI / Math.Pow(h, 2);
Ke[5, 2] = 2 * EI / Math.Pow(h, 1);
Ke[5, 3] = 0;
Ke[5, 4] = -6 * EI / Math.Pow(h, 2);
Ke[5, 5] = 4 * EI / Math.Pow(h, 1);
// Формирование локальной матрицы масс
Me[0, 0] = h / 3;
Me[0, 1] = 0;
Me[0, 2] = 0;
Me[0, 3] = h / 6;
Me[0, 4] = 0;
Me[0, 5] = 0;
Me[1, 0] = 0;
Me[1, 1] = 13.0 / 35 * h;
Me[1, 2] = 11.0 / 210 * h * h;
Me[1, 3] = 0;
Me[1, 4] = 9.0 / 70 * h;
Me[1, 5] = -13.0 / 420 * h * h;
Me[2, 0] = 0;
Me[2, 1] = 9.0 / 70 * h;
Me[2, 2] = 1.0 / 105 * h * h * h;
Me[2, 3] = 0;
Me[2, 4] = 13.0 / 420 * h * h;
Me[2, 5] = -1.0 / 140 * h * h * h;
Me[3, 0] = h / 6;
Me[3, 1] = 0;
Me[3, 2] = 0;
Me[3, 3] = h / 3;
Me[3, 4] = 0;
Me[3, 5] = 0;
Me[4, 0] = 0;
Me[4, 1] = 9.0 / 70 * h;
Me[4, 2] = 13.0 / 420 * h * h;
Me[4, 3] = 0;
Me[4, 4] = 13.0 / 35 * h;
Me[4, 5] = -11.0 / 210 * h * h;
Me[5, 0] = 0;
Me[5, 1] = -13.0 / 420 * h * h;
Me[5, 2] = -1.0 / 140 * h * h * h;
Me[5, 3] = 0;
Me[5, 4] = -11.0 / 210 * h * h;
Me[5, 5] = 1.0 / 105 * h * h * h;
for (int i = 0; i < 6; i++)
for (int j = 0; j < 6; j++)
Me[i, j] = Me[i, j] * mm;
// Матрица для приведения распределенных сил к узловым
Ht[0, 0] = h / 3;
Ht[0, 1] = 0;
Ht[0, 2] = h / 6;
Ht[0, 3] = 0;
Ht[1, 0] = 0;
Ht[1, 1] = 7.0 / 20 * h;
Ht[1, 2] = 0;
Ht[1, 3] = 3.0 / 20 * h;
Ht[2, 0] = 0;
Ht[2, 1] = 1.0 / 20 * h * h;
Ht[2, 2] = 0;
Ht[2, 3] = 1.0 / 30 * h * h;
Ht[3, 0] = h / 6;
Ht[3, 1] = 0;
Ht[3, 2] = h / 3;
Ht[3, 3] = 0;
Ht[4, 0] = 0;
Ht[4, 1] = 7.0 / 20 * h;
Ht[4, 2] = 0;
Ht[4, 3] = 3.0 / 20 * h;
Ht[5, 0] = 0;
Ht[5, 1] = -1.0 / 20 * h * h;
Ht[5, 2] = 0;
Ht[5, 3] = -1.0 / 30 * h * h;
// Формирование вектор столбца сил в локальной системе элемента
for (int j = 0; j < 6; j++)
{
Qp[j] = 0;
for (int k = 0; k < 4; k++)
Qp[j] = Qp[j] + Ht[j, k] * pxy[ii, k];
}
//Преобразование матриц в глобальную систему
for (int i = 0; i < 6; i++)
for (int j = 0; j < 6; j++)
Tt[j, i] = T[i, j];
for (int i = 0; i < 6; i++)
{
for (int j = 0; j < 6; j++)
{
TtK[i, j] = 0;
TtM[i, j] = 0;
for (int k = 0; k < 6; k++)
{
TtK[i, j] = TtK[i, j] + Tt[i, k] * Ke[k, j];
TtM[i, j] = TtM[i, j] + Tt[i, k] * Me[k, j];
}
}
}
for (int i = 0; i < 6; i++)
{
for (int j = 0; j < 6; j++)
{
Ke1[i, j] = 0;
Me1[i, j] = 0;
for (int k = 0; k < 6; k++)
{
Ke1[i, j] = Ke1[i, j] + TtK[i, k] * T[k, j];
Me1[i, j] = Me1[i, j] + TtM[i, k] * T[k, j];
}
}
}
for (int j = 0; j < 6; j++)
{
Qpxy[ii, j] = 0;
for (int k = 0; k < 6; k++)
{
Qpxy[ii, j] = Qpxy[ii, j] + Tt[j, k] * Qp[k];
}
}
for (int i = 1; i <= 6; i++)
{
int ig = A[ii, i];
P[ig - 1] = P[ig - 1] + Qpxy[ii, i - 1];
for (int j = 1; j <= 6; j++)
{
int jg = A[ii, j];
K[ig - 1, jg - 1] = K[ig - 1, jg - 1] + Ke1[i - 1, j - 1];
M[ig - 1, jg - 1] = M[ig - 1, jg - 1] + Me1[i - 1, j - 1];
}
}
}
//Копирование матрицы жесткости в K1
for (int i = 0; i < f1.n * 3; i++)
for (int j = 0; j < f1.n * 3; j++)
{
K1[i, j] = K[i, j];
// dataGridView1.Rows[i].Cells[j].Value = K1[i, j];
}
//Добавление динамической составляющей
for (int i = 0; i < f1.n * 3; i++)
for (int j = 0; j < f1.n * 3; j++)
{
K1[i, j] = K[i, j] - w * w * M[i, j];
//dataGridView1.Rows[i].Cells[j].Value = K1[i, j];
}
for (int i = 0; i < f1.n; i++)
{
//Наложение главных граничных условий для подвижных соединений
if (Convert.ToInt32(f1.MatrCoor[i, 6]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 6]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh, j] = K1[3 * sh, j] + K1[3 * i, j];
K1[3 * i, j] = 0;
}
P[3 * sh] = P[3 * i] + P[3 * sh];
P[3 * i] = 0;
K1[3 * i, 3 * sh] = -1.0;
K1[3 * i, 3 * i] = 1.0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 7]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 7]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh + 1, j] = K1[3 * sh + 1, j] + K1[3 * i + 1, j];
K1[3 * i + 1, j] = 0;
}
P[3 * sh + 1] = P[3 * i + 1] + P[3 * sh + 1];
P[3 * i + 1] = 0;
K1[3 * i + 1, 3 * sh + 1] = -1.0;
K1[3 * i + 1, 3 * i + 1] = 1.0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 8]) > 0)
{
int sh = Convert.ToInt32(f1.MatrCoor[i, 8]) - 1;
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * sh + 2, j] = K1[3 * sh + 2, j] + K1[3 * i + 2, j];
K1[3 * i + 2, j] = 0;
}
P[3 * sh + 2] = P[3 * i + 2] + P[3 * sh + 2];
P[3 * i + 2] = 0;
K1[3 * i + 2, 3 * sh + 2] = -1.0;
K1[3 * i + 2, 3 * i + 2] = 1.0;
}
}
for (int i = 0; i < f1.n; i++)
{
//Наложение главных граничных условий для неподвижных опор
if (Convert.ToInt32(f1.MatrCoor[i, 6]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i, j] = 0;
}
K1[3 * i, 3 * i] = K[3 * i, 3 * i];
P[3 * i] = 0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 7]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i + 1, j] = 0;
}
K1[3 * i + 1, 3 * i + 1] = K[3 * i + 1, 3 * i + 1];
P[3 * i + 1] = 0;
}
if (Convert.ToInt32(f1.MatrCoor[i, 8]) < 0)
{
for (int j = 0; j < f1.n * 3; j++)
{
K1[3 * i + 2, j] = 0;
}
K1[3 * i + 2, 3 * i + 2] = K[3 * i + 2, 3 * i + 2];
P[3 * i + 2] = 0;
}
}
for (int i = 0; i < f1.n * 3; i++)
{
P1[i] = P[i];
}
int KS = 0;
ClassSIMQ S = new ClassSIMQ();
S.SIMQ(K1, ref P1, f1.n * 3, ref KS);
label2.Text = "Код ошибки равен " + KS.ToString();
f1.q = new double[f1.n * 3];
f1.q = P1;
//Реакции и узловые внешние силы
double[] D = new double[f1.n * 3];
for (int i = 0; i < f1.n * 3; i++)
{
D[i] = 0;
for (int j = 0; j < f1.n * 3; j++)
{
D[i] = D[i] + K[i, j] * f1.q[j];
}
}
//Проверка
double[] D1 = new double[f1.n * 3];
for (int i = 0; i < f1.n * 3; i++)
{
D1[i] = -P[i];
for (int j = 0; j < f1.n * 3; j++)
{
D1[i] = D1[i] + K1[i, j] * f1.q[j];
}
}
int signal = 0;
if (f1.radioButton1.Checked) signal = 1;
if (f1.radioButton2.Checked) signal = 2;
if (f1.radioButton3.Checked) signal = 3;
switch (signal)
{
case 1:
//Вывод матрицы жесткости в таблицу
for (int i = 0; i < f1.n * 3; i++)
for (int j = 0; j < f1.n * 3; j++)
{
dataGridView1.Rows[i].Cells[j].Value = K1[i, j];
}
label1.Text = " Матрица жесткости";
break;
case 2:
for (int i = 0; i < f1.n * 3; i++)
{
dataGridView1.Rows[i].Cells[1].Value = P1[i];
}
for (int i = 0; i < f1.n * 3; i++)
{
dataGridView1.Rows[i].Cells[0].Value = (i+3)/3;
dataGridView1.Rows[i].Cells[2].Value = D[i];
}
label1.Text = " Перемещения узлов и внешние силы";
break;
case 3:
for (int i = 0; i < f1.n * 3; i++)
{
dataGridView1.Rows[i].Cells[0].Value = D1[i];
}
label1.Text = " Проверка равновесия узлов";
break;
default:
String Str = "Выберите результат вычислений";
//Вывод сообщения
MessageBox.Show(Str, "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Warning);
return;
}
}
}
}
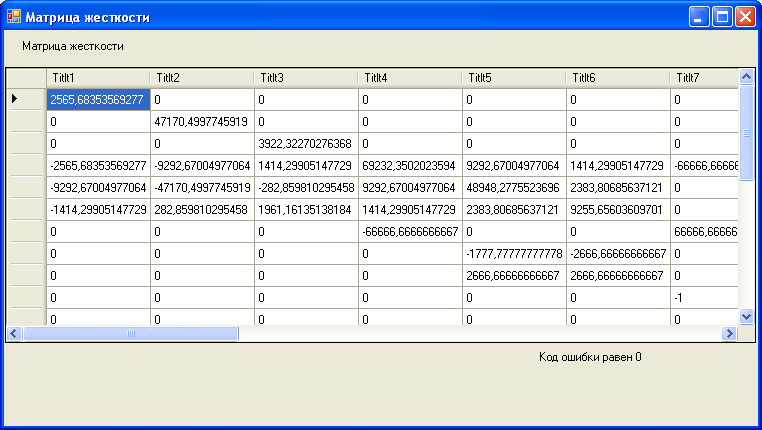
Рис. 6. Форма проекта, представляющая матрицы системы, – форма 2.
Форма3
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.Drawing.Drawing2D;
namespace Рама
{
public partial class Form3: Form
{
Form1 f1;
public Form2 f2;
double[,] NQMM;
public Form3(Form1 f1)
{
InitializeComponent();
this.f1 = f1;
f2 = f1.f2;
NQMM=new double[f1.m,5];
NQM();
}
void NQM()
{
if (f2 == null) return;
// массивы косинусов
double[] CA = new double[f1.m];
double[] CB = new double[f1.m];
//dataGridView1.Rows.Add();
//dataGridView1.Rows[0].Cells[0].Value = f2.K[1,1];
for (int ii = 0; ii < f1.m; ii++)
{
NQMM[ii, 0] = ii + 1;
double[] qe = new double[6];
double[] qe1 = new double[6];
double[] u = new double[3];
for (int i=0;i<6;i++)
{
qe1[i]=f1.q[f2.A[ii,i+1]-1];
}
double [,] Ke = new double[3, 3];
// double[,] Ke1 = new double[6, 6];
// double[,] Me = new double[6, 6];
// double[,] Me1 = new double[6, 6];
double[,] T = new double[6, 6];
// double[,] Tt = new double[6, 6];
// double[,] TtK = new double[6, 6];
// double[,] TtM = new double[6, 6];
double x1 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 1]) - 1, 1];
double y1 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 1]) - 1, 2];
double x2 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 2]) - 1, 1];
double y2 = f1.MatrCoor[Convert.ToInt32(f1.MatrTop[ii, 2]) - 1, 2];
double h = Math.Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
double cosA = (x2 - x1) / h;
double cosB = (y2 - y1) / h;
double EF = f1.MatrTop[ii, 7];
double EI = f1.MatrTop[ii, 8];
double mm = f1.MatrTop[ii, 9];
CA [ii]=cosA;
CB[ii] = cosB;
//Матрица преобразования координат
T[0, 0] = cosA;
T[0, 1] = cosB;
T[0, 2] = 0;
T[0, 3] = 0;
T[0, 4] = 0;
T[0, 5] = 0;
T[1, 0] = -cosB;
T[1, 1] = cosA;
T[1, 2] = 0;
T[1, 3] = 0;
T[1, 4] = 0;
T[1, 5] = 0;
T[2, 0] = 0;
T[2, 1] = 0;
T[2, 2] = 1;
T[2, 3] = 0;
T[2, 4] = 0;
T[2, 5] = 0;
T[3, 0] = 0;
T[3, 1] = 0;
T[3, 2] = 0;
T[3, 3] = cosA;
T[3, 4] = cosB;
T[3, 5] = 0;
T[4, 0] = 0;
T[4, 1] = 0;
T[4, 2] = 0;
T[4, 3] = -cosB;
T[4, 4] = cosA;
T[4, 5] = 0;
T[5, 0] = 0;
T[5, 1] = 0;
T[5, 2] = 0;
T[5, 3] = 0;
T[5, 4] = 0;
T[5, 5] = 1;
//Локальная матрица жесткости 3*3
Ke[0, 0] = EF / h;
Ke[0, 1] = 0;
Ke[0, 2] = 0;
Ke[1, 0] = 0;
Ke[1, 1] = 12 * EI / Math.Pow(h, 3);
Ke[1, 2] = 6 * EI / Math.Pow(h, 2);
Ke[2, 0] = 0;
Ke[2, 1] = 6 * EI / Math.Pow(h, 2);
Ke[2, 2] = 4 * EI / Math.Pow(h, 1);
// вычисление перемещений в локальной системе отсчета
for (int i = 0; i < 6; i++)
{
qe[i] = 0;
for (int k = 0; k < 6; k++)
qe[i] = qe[i] + T[i, k] * qe1[k];
}
// Вычисление относительных локальных перемещений
double[] deltau = new double[3];
deltau[0]=qe[3]-qe[0];
deltau[1]=qe[5]*h-(qe[4]-qe[1]);
deltau[2]=qe[2]-qe[5];
for (int i = 0; i < 3; i++)
{
NQMM[ii,i+1]=0;
for (int k = 0; k < 3; k++)
NQMM[ii, i + 1] = NQMM[ii, i + 1] + Ke[i, k] * deltau[k];
}
//Изменение знака внутреннего усилия в первом узле
//в соответствие срастяжением нижних волокон при M>0
NQMM[ii, 3] = -NQMM[ii, 3];
dataGridView1.Rows.Add();
//Определение момента во втором узле элемента
NQMM[ii, 4] = NQMM[ii, 3] + NQMM[ii, 2] * h;
for (int i = 0; i < 5; i++)
{
dataGridView1.Rows[ii].Cells[i].Value = NQMM[ii, i];
}
}
//Построение
double[] x, y;
Double My = 0, MaxY = 0, Mx = 0, MaxX = 0;
int[] yint, xint;
Bitmap myBmp;
x = new double[f1.n];
y = new double[f1.n];
for (int i = 0; i < f1.n; i++)
{
x[i] = f1.MatrCoor[i, 1];
y[i] = f1.MatrCoor[i, 2];
}
if (x == null || y == null) return;
MaxY = 0.001;
MaxX = 0.001;
for (int i = 0; i < f1.n; i++)
{
if (System.Math.Abs(y[i]) > MaxY)
{
MaxY = System.Math.Abs(y[i]);;
}
if (System.Math.Abs(x[i]) > MaxX)
{
MaxX = System.Math.Abs(x[i]);
}
}
if (MaxY >= MaxX)
MaxX = MaxY;
else
MaxY = MaxX;
My = (pictureBox1.Height) / 1.2 / MaxY;
Mx = (pictureBox1.Width) / 1.2 / MaxX;
yint = new int[f1.n];
xint = new int[f1.n];
for (int i = 0; i < f1.n; i++)
{
yint[i] = Convert.ToInt32(pictureBox1.Height / 1.1) - Convert.ToInt32(y[i] * My);
xint[i] = Convert.ToInt32(pictureBox1.Width / 10) + Convert.ToInt32(x[i] * Mx);
}
myBmp = new Bitmap(pictureBox1.Width, pictureBox1.Height);
Graphics gr1 = Graphics.FromImage(myBmp);
Pen P1 = new Pen(Color.Red, 2);
gr1.DrawRectangle(P1, 1, 1, pictureBox1.Width - 2, pictureBox1.Height - 2);
Pen P2 = new Pen(Color.Green, 2);
Pen P5 = new Pen(Color.Green, 12);
Brush B2 = new SolidBrush(Color.Azure);
Brush B3 = new SolidBrush(Color.Brown);
int[] Zakx = new int[f1.n];
int[] Zaky = new int[f1.n];
int[] ZakFi = new int[f1.n];
for (int i = 0; i < f1.n; i++)
{
Zakx[i] = Convert.ToInt32(f1.MatrCoor[i, 6]);
Zaky[i] = Convert.ToInt32(f1.MatrCoor[i, 7]);
ZakFi[i] = Convert.ToInt32(f1.MatrCoor[i, 8]);
}
Pen P3 = new Pen(Color.Brown, 4);
Pen P6 = new Pen(Color.Aqua, 18);
for (int i = 0; i < f1.m; i++)
{
//Построение распределенной нагрузки
if ((f1.MatrTop[i, 3]!= 0) || (f1.MatrTop[i, 4]!= 0) || (f1.MatrTop[i, 5]!= 0) || (f1.MatrTop[i, 6]!= 0))
{
gr1.DrawLine(P6, xint[(int)f1.MatrTop[i, 1] - 1], yint[(int)f1.MatrTop[i, 1] - 1], xint[(int)f1.MatrTop[i, 2] - 1], yint[(int)f1.MatrTop[i, 2] - 1]);
}
//Построение линий конечных элементов
gr1.DrawLine(P3, xint[(int)f1.MatrTop[i, 1] - 1], yint[(int)f1.MatrTop[i, 1] - 1], xint[(int)f1.MatrTop[i, 2] - 1], yint[(int)f1.MatrTop[i, 2] - 1]);
}
//Нанесение прямоугольников на расположение узлов
for (int i = 0; i < f1.n; i++)
{
gr1.FillRectangle(B3, xint[i] - 4, yint[i] - 4, 8, 8);
gr1.DrawRectangle(P2, xint[i] - 4, yint[i] - 4, 8, 8);
}
// Линии шириной 12 п. в точках закрепления
for (int i = 0; i < f1.n; i++)
{
if (Zakx[i] < 0 || Zaky[i] < 0)
{
gr1.DrawLine(P5, xint[i] - 24, yint[i] + 10, xint[i] + 24, yint[i] + 10);
}
//Нанесение окружностей на расположение шарниров
if ((Zakx[i]!= 0 || Zaky[i]!= 0) & (ZakFi[i] == 0))
{
gr1.FillEllipse(B2, xint[i] - 6, yint[i] - 6, 12, 12);
gr1.DrawEllipse(P2, xint[i] - 6, yint[i] - 6, 12, 12);
}
}
double Mp = 0, MaxP = 0.001, P = 0;
double[] Px = new double[f1.n];
double[] Py = new double[f1.n];
double[] PM = new double[f1.n];
int[] intPx = new int[f1.n];
int[] intPy = new int[f1.n];
Pen P4 = new Pen(Color.Indigo, 6);
// Стиль пера с наконечниками
P4.SetLineCap(LineCap.Flat, LineCap.ArrowAnchor, DashCap.Flat);
//Изображение сил и моментов
for (int i = 0; i < f1.n; i++)
{
Px[i] = f1.MatrCoor[i, 3];
Py[i] = f1.MatrCoor[i, 4];
PM[i] = f1.MatrCoor[i, 5];
P = Math.Sqrt(Px[i] * Px[i] + Py[i] * Py[i]);
if (MaxP <= P)
MaxP = P;
}
Mp = pictureBox1.Width / 8 / MaxP;
for (int i = 0; i < f1.n; i++)
{
intPy[i] = Convert.ToInt32(Py[i] * Mp);
intPx[i] = Convert.ToInt32(Px[i] * Mp);
}
for (int i = 0; i < f1.n; i++)
{
if (intPx[i]!= 0 || intPy[i]!= 0)
{
gr1.DrawLine(P4, xint[i], yint[i], xint[i] + intPx[i], yint[i] - intPy[i]);
}
if (PM[i] > 0)
{
gr1.DrawArc(P4, xint[i] - 20, yint[i] - 20, 40, 40, 0, -150);
}
if (PM[i] < 0)
{
gr1.DrawArc(P4, xint[i] - 20, yint[i] - 20, 40, 40, 0, 150);
}
}
//Построение эпюры моментов
double[] M1, M2;
M1 = new double[f1.m];
M2 = new double[f1.m];
int[] intM1 = new int[f1.m];
int[] intM2 = new int[f1.m];
double MashtabM = 0, MaxM=0;
for (int i = 0; i < f1.m; i++)
{
M1[i] = NQMM[i, 3];
M2[i] = NQMM[i, 4];
}
for (int i = 0; i < f1.m; i++)
{
if (System.Math.Abs(M1[i]) > MaxM)
{
MaxM = System.Math.Abs(M1[i]);;
}
if (System.Math.Abs(M2[i]) > MaxM)
{
MaxM = System.Math.Abs(M2[i]);
}
}
// 40 пиксклей - максимальное значение на эпюре моментов
MashtabM = 40.0 / MaxM;
for (int i = 0; i < f1.m; i++)
{// Относительная ось моментов направлена вниз, противоположно оси Q
intM1[i] = -Convert.ToInt32(NQMM[i, 3] * MashtabM);
intM2[i] = -Convert.ToInt32(NQMM[i, 4] * MashtabM);
}
Pen P13 = new Pen(Color.Brown, 2);
for (int i = 0; i < f1.m; i++)
{
int xM1=-Convert.ToInt32(intM1[i]*CB[i]);
int xM2 = -Convert.ToInt32(intM2[i] * CB[i]);
int yM1 = -Convert.ToInt32(intM1[i] * CA[i]);
int yM2 = -Convert.ToInt32(intM2[i] * CA[i]);
gr1.DrawLine(P13, xint[(int)f1.MatrTop[i, 1] - 1], yint[(int)f1.MatrTop[i, 1] - 1], xint[(int)f1.MatrTop[i, 1] - 1] +xM1, yint[(int)f1.MatrTop[i, 1] - 1]+yM1);
gr1.DrawLine(P13, xint[(int)f1.MatrTop[i, 2] - 1], yint[(int)f1.MatrTop[i, 2] - 1], xint[(int)f1.MatrTop[i, 2] - 1]+xM2, yint[(int)f1.MatrTop[i, 2] - 1] +yM2);
gr1.DrawLine(P13, xint[(int)f1.MatrTop[i, 1] - 1] + xM1, yint[(int)f1.MatrTop[i, 1] - 1] + yM1, xint[(int)f1.MatrTop[i, 2] - 1] + xM2, yint[(int)f1.MatrTop[i, 2] - 1] + yM2);
}
pictureBox1.Image = myBmp;
}
}
}
Рис. 7. Форма проекта, отражающая внутренние силовые факторы, – форма 3.
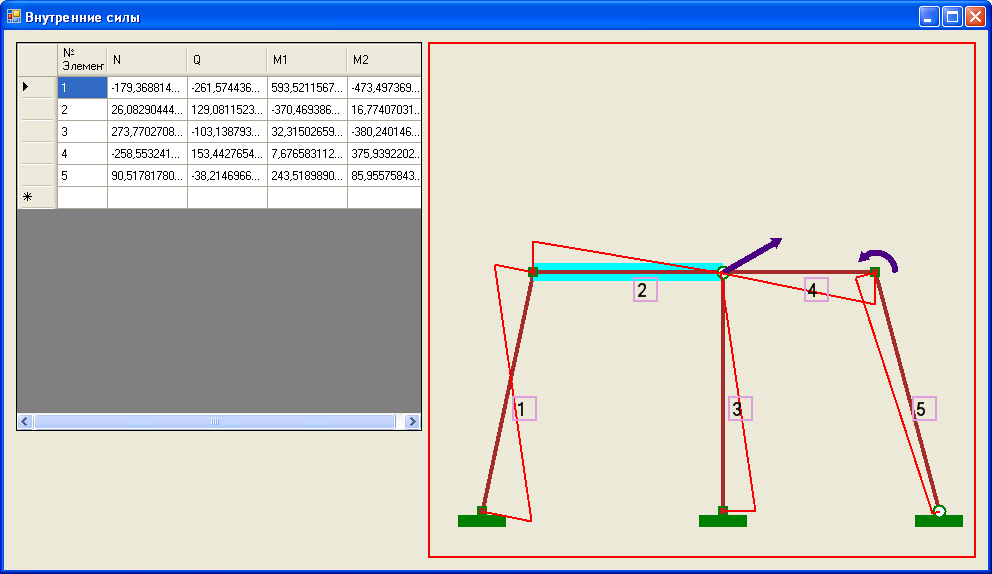
Рис. 8. Форма проекта, отражающая внутренние силовые факторы в динамике при частоте 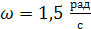 , – форма 3.
, – форма 3.
Варианты заданий:
Определить внутренние силовые факторы в элементах и перемещения узлов плоской рамы в случае статического приложения сил и при заданном гармоническом воздействии при частоте 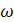 .
.
Механическая системы, содержащей рамные конечные элементы (рис. 9,10,11), к которой приложены распределенные силы интенсивности p, сосредоточенные сила F и момент M (в статике и в динамике при частоте гармонического воздействия всех сил в одной фазе 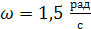 ). Известны размеры
). Известны размеры 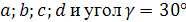 (Таблица 4). Жесткость стержней на растяжение-сжатие составляет EF=
(Таблица 4). Жесткость стержней на растяжение-сжатие составляет EF= 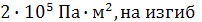 EI=4000
EI=4000 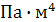 . Удельная масса стержней рамы m=100 кг/м.
. Удельная масса стержней рамы m=100 кг/м.
Таблица 4. Варианты заданий.
| № Варианта | Схема | F, Н | M, Н 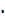 м м
| p, Н/м | a, м | b, м | c, м | d, м |
| рис. 9 | - | |||||||
| рис. 9 | - | |||||||
| рис. 9 | 1,5 | - | ||||||
| рис. 9 | - | |||||||
| рис. 10 | - | |||||||
| рис. 10 | - | |||||||
| рис. 10 | 1,5 | - | ||||||
| рис. 10 | - | |||||||
| рис. 11 | ||||||||
| рис. 11 | ||||||||
| рис. 11 | 1,5 | |||||||
| рис. 11 |
p=40 Н/м, сосредоточенные сила F=700 Н и момент M=200 Н 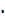 м (в статике и в динамике при частоте гармонического воздействия всех сил в одной фазе
м (в статике и в динамике при частоте гармонического воздействия всех сил в одной фазе 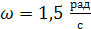 ). Известны размеры
). Известны размеры 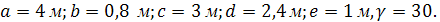
Рис. 9. Варианты 1,2,3,4.
Рис. 10. Варианты 5,6,7,8.
Рис. 11. Варианты 9,10,11,12.