Основные теоремы дифференциального исчисления лежат в основе исследования функций с помощью производных.
Теорема Ферма. Если дифференцируемая на отрезке [а,b] функция y=f(x) достигает своего наибольшего или наименьшего значения внутри отрезка в некоторой точке х=c, то производная в этой точке равна нулю: f /(c) = 0.
| у у/= 0 О a c b х |
| у у/= 0 f(a)=f(b) О a с b х |
Геометрический смысл теоремы Ролля заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), принимающей на концах этого отрезка равные значения f(a)=f(b), существует такая точка х=с внутри отрезка, в которой касательная к графику функции в этой точке параллельна оси Ох.
| у В А О a с b х |
f /(c) =  .
.
Геометрический смысл теоремы Лагранжа заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), существует такая точка х=с внутри отрезка [а,b], в которой касательная к графику функции в этой точке параллельна секущей, соединяющей график на концах отрезка.
Функция f(x) называется монотонной на интервале, если она на нем или только возрастает, или только убывает.
| у у./=0 возр. убыв. у¢>0 у¢<0 0 х0 х |
Если функция монотонно убывает на интервале, то большему значению аргумента х2>x1, соответствует меньшее значение функции: f(x2)<f(x1).
На рисунке на интервале 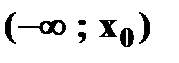 функция монотонно возрастает, а на интервале
функция монотонно возрастает, а на интервале  монотонно убывает.
монотонно убывает.
Введем обозначения Dх = х2 - х1 - приращение аргумента и приращение функции:  у = f(x2) - f(x1). Для возрастающей функции приращения аргумента и функции имеют одинаковые знаки, а следовательно, отношение
у = f(x2) - f(x1). Для возрастающей функции приращения аргумента и функции имеют одинаковые знаки, а следовательно, отношение  >0. Для убывающей функции приращения аргумента и функции имеют противоположные знаки, а следовательно, отношение
>0. Для убывающей функции приращения аргумента и функции имеют противоположные знаки, а следовательно, отношение 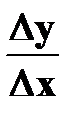 < 0. Так как первая производная функции равна
< 0. Так как первая производная функции равна  , то по знаку производной можно определять участки возрастания и убывания функции.
, то по знаку производной можно определять участки возрастания и убывания функции.
Теорема 1. Если функция у=f(x) дифференцируема на интервале  и ее производная положительна у¢>0, то функция на этом интервале монотонно возрастает, а если производная отрицательна у¢<0, то функция на интервале монотонно убывает.
и ее производная положительна у¢>0, то функция на этом интервале монотонно возрастает, а если производная отрицательна у¢<0, то функция на интервале монотонно убывает.
Отметим, что если в точках первая производная равна нулю или не существует, то в этих точках функция не возрастает и не убывает. Здесь возможны:
- точки перегиба, в которых выпуклость графика функции сменяется вогнутостью или наоборот;
- точки локального экстремума, в которых участок возрастания функции сменяется участком убывания или наоборот.
Точки, в которых первая производная либо равна нулю, либо не существует, называются критическими точками I рода.
| у у¢= 0 у¢>0 у¢<0 у¢>0 у¢<0 "+" "-" "+" "-" у¢= 0 0 х1к х2к х3к х |
 f(x0) (или f(x)
f(x0) (или f(x)  f(x0)).
f(x0)).
Точки локального максимума или минимума объединены общим названием - точками локального экстремума функции.
Отметим, что в точках локального экстремума функция достигает своего наибольшего или наименьшего значения лишь в некоторой локальной области. Возможны случаи, когда по значению уmax  уmin.
уmin.
Теорема 2. Если непрерывная функция у = f(x) имеет в точке х0 локальный экстремум, то в этой точке первая производная либо равна нулю, либо не существует, т.е. локальный экстремум имеет место в критических точках I рода.
В точках локального экстремума либо касательная параллельна оси 0х, либо имеются две касательные (см. рис.). Отметим, что критические точки являются необходимым, но недостаточным условием локального экстремума. Локальный экстремум имеет место только в критических точках I рода, но не во всех критических точках имеет место локальный экстремум.
Например: кубическая парабола у = х3, имеет критическую точка х0=0, в которой производная у/(0)=0, но критическая точка х0=0 не является точкой экстремума, а в ней имеет место точка перегиба (см. ниже).
Теорема 3. Если при переходе аргумента через критическую точку I рода слева направо первая производная у / (x)
1) меняет знак с “+” на “-”, то непрерывная функция у(х) в этой критической точке имеет локальный максимум;
2) меняет знак с “-” на “+”, то непрерывная функция у(х) имеет в этой критической точке локальный минимум
3) не меняет знак, то в этой критической точке нет локального экстремума, здесь имеет место точка перегиба.
Для локального максимума область возрастания функции (у/  0) сменяется на область убывания функции (у/
0) сменяется на область убывания функции (у/  0). Для локального минимума область убывания функции (у/
0). Для локального минимума область убывания функции (у/  0) сменяется на область возрастания функции (у /
0) сменяется на область возрастания функции (у /  0).
0).
| у у=х3 О х |
Так график кубической параболы у=х3 на интервале  выпуклый и лежит ниже своих касательных, а на интервале
выпуклый и лежит ниже своих касательных, а на интервале  вогнутый и лежит выше своих касательных.
вогнутый и лежит выше своих касательных.
Отметим, что выпуклость и вогнутость графика функции можно определять по знаку её второй производной. Для кубической параболы у=х3 график на интервале  выпуклый, а вторая производная на этом интервале отрицательна у//=(3x2)/=6x<0(при x<0). На интервале
выпуклый, а вторая производная на этом интервале отрицательна у//=(3x2)/=6x<0(при x<0). На интервале  её график вогнутый, а вторая производная на этом интервале положительна у//=6x>0(при x>0). Это связано с тем, что вторая производная определяет поведение первой производной. Для выпуклого участка угловой коэффициент касательной, который определяется первой производной, убывает, а следовательно вторая производная отрицательна, а для вогнутого участка наоборот угловой коэффициент касательной возрастает, а следовательно вторая производная положительная.
её график вогнутый, а вторая производная на этом интервале положительна у//=6x>0(при x>0). Это связано с тем, что вторая производная определяет поведение первой производной. Для выпуклого участка угловой коэффициент касательной, который определяется первой производной, убывает, а следовательно вторая производная отрицательна, а для вогнутого участка наоборот угловой коэффициент касательной возрастает, а следовательно вторая производная положительная.
Теорема 4. Если на интервале (а;b) вторая производная непрерывной функции положительна у//>0, то график функции вогнутый, а если вторая производная отрицательна у//<0, то график функции выпуклый.
Точка, отделяющая выпуклую часть от вогнутой, называется точкой перегиба.
Теорема 5. Если непрерывная функция y=f(x) имеет точку перегиба хп, то в этой точке вторая производная равна нулю (у//=0) или не существует.
Точки, в которых вторая производная равна нулю (у//=0) или не существует называются критическими точками второго рода.
Согласно теоремы точки перегиба бывают только в критических точках второго рода, но не во всех в критических точках второго рода имеют место точки перегиба.
Теорема 6. Если при переходе аргументом через критическую точку второго рода хп вторая производная меняет знак, то эта критическая точка является точкой перегиба.
Так кубическая парабола у=х3 имеет точку перегиба хп=0, в которой её вторая производная у//=6хп=0 и при переходе через эту точку вторая производная меняет знак с «-» на «+».
При исследовании поведения функций на бесконечности при х®∞ или вблизи точек бесконечного разрыва второго рода, когда у®∞ часто оказывается, что график функции неограниченно близко приближается к некоторой прямой.
Прямые к которым неограниченно близко приближаются графики функций называются асимптотами.
Асимптоты бывают трех видов: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты имеют место в точках бесконечного разрыва второго рода, когда пределы в этих точках равны бесконечности.
Прямая х=а называется вертикальной асимптотой графика функции у=f(x), если стремится к бесконечности хотя бы один из пределов: правый  или левый
или левый  .
.
| у О х=1 х |
Пример. Функция  неопределена при
неопределена при
х-1=0 или х=1. В этой точке функция терпит бесконечный разрыв второго рода, т.к.  -левый предел;
-левый предел;  -правый предел. Прямая х=1 является вертикальной асимптотой.
-правый предел. Прямая х=1 является вертикальной асимптотой.
Здесь же отметим, что на бесконечности при х®±∞ эта функция стремится к нулю: у=f(x) ® 0, т.к.  =0. Горизонтальная прямая у=0, к которой стремится функция на бесконечности называется горизонтальной асимптотой.
=0. Горизонтальная прямая у=0, к которой стремится функция на бесконечности называется горизонтальной асимптотой.
Прямая у=b называется горизонтальной асимптотой графика функции у=f(x) при х®±∞, если равен числу b любой из пределов:  .
.
Отметим, что эти пределы могут быть разными  , а следовательно имеют место две горизонтальные асимптоты y=b1и y=b2.
, а следовательно имеют место две горизонтальные асимптоты y=b1и y=b2.
Существуют также наклонные асимтоты.
Прямая у=kx+b называется наклонной асимптотой графика функции y=f(x) при х ®±∞, если равен нулю любой из пределов  .
.
Теорема 7. Для того, чтобы график функции y=f(x) имел наклонную асимптоту необходимо и достаточно, чтобы одновременно существовали по два конечных предела  .
.
С помощью этих пределов определяются параметры (k и b) наклонных асимптот. Причем пределы при х® - ∞ и при х® + ∞ вычисляются раздельно, т.к. возможны две разные наклонные асимптоты у=k1x+b1 и y= k2x+b2.
Отметим, что горизонтальная асимптота у=b является частным случаем наклонной асимптоты, когда  .
.
Приведем план полного исследования функции с помощью производной:
1. Найти область определения функции;
2. Найти точки пересечения графика с осями координат, нули функции и интервалы знакопостоянства; четность, нечетность;
3. Найти асимптоты графика функции; исследовать поведение функции в точках разрыва;
4. Найти критические точки и исследовать функцию на монотонность;
5. Найти точки перегиба и промежутки выпуклости.
Примеры: 1) Построить график функции  .
.
1. Область определения функции – вся числовая ось, то есть  .
.
2. Точки пересечения графика с координатными осями будут: с осью Oy –
(0;-2); с осью Ox:y=0, тогда  ,
,
 при х=-1, х
при х=-1, х  -2,7, х
-2,7, х  0,7.
0,7.
3. График функции асимптот не имеет, так как  .
.
4. Найдем критические точки:
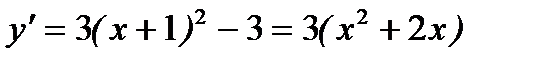 Производная равна нулю при х=0 и х=-2. Результаты исследования функции на монотонность сведем в таблицу
Производная равна нулю при х=0 и х=-2. Результаты исследования функции на монотонность сведем в таблицу
| x | 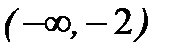
| -2 | (-2; 0) | 
| |

| + | – | + | ||
| y | 
| 
| -2 | 
|
Таким образом,  – точка максимума,
– точка максимума,  , точка х=0 – точка минимума,
, точка х=0 – точка минимума,  .
.
5. Исследуем график функции на выпуклость и вогнутость. Найдем  :
:  .
.  при х = –1. Результаты исследования отразим в таблице
при х = –1. Результаты исследования отразим в таблице
| x | 
| -1 | 
|

| – | + | |
| y | 
| 0 т.п. | 
|
Точка с абсциссой х =–1 – точка перегиба. График на рисунке 1.
2) Построить график функции  .
.
1. Знаменатель дроби обращается в ноль при  , поэтому область определения будет иметь вид
, поэтому область определения будет иметь вид  .
.
2. Так как y=0 при x=0, то график функции проходит через начало координат. Функция принимает положительные значения в интервалах  и
и  , и отрицательные значения в интервалах
, и отрицательные значения в интервалах  и
и  .
.
Функция является нечетной, так как  . Следовательно, график функции симметричен относительно начала координат.
. Следовательно, график функции симметричен относительно начала координат.

Рис. 1 Рис.2
3. Так как  и
и 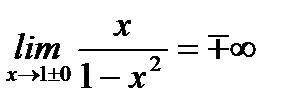 , то прямые x=1, x=-1 являются вертикальными асимптотами.
, то прямые x=1, x=-1 являются вертикальными асимптотами.
Выясним наличие наклонных асимптот: 
 . Тогда
. Тогда 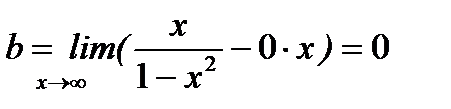 . Следовательно, прямая y=0 ( ось Ox) является горизонтальной асимптотой.
. Следовательно, прямая y=0 ( ось Ox) является горизонтальной асимптотой.
4. Найдем интервалы возрастания и убывания.  . Так как,
. Так как, 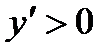 при любом х из области определения функции, то функция не имеет экстремумов и монотонно возрастает в каждом из интервалов
при любом х из области определения функции, то функция не имеет экстремумов и монотонно возрастает в каждом из интервалов  .
.
5. Найдем интервалы выпуклости и точку перегиба.
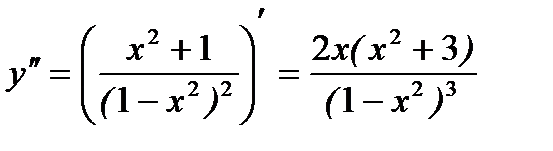 . Вторая производная равна нулю при х=0.
. Вторая производная равна нулю при х=0.
| x | 
| -1 | (-1;0) | (0; 1) | 
| ||
| у" | + | Не сущ | – | + | Не сущ. | – | |
| y | 
| Не сущ | 
| 
| Не сущ. | 
|
Точка с координатами О(0;0) – точка перегиба. График на рисунке 2.
Индивидуальные задания
Вариант 1
1. Провести полное исследование и построить графики функций:
а) y =  (12x – x3) б) y =
(12x – x3) б) y = 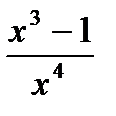
2. Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен 15м. При каком радиусе полукруга окно будет пропускать наибольшее количество света?
Вариант 2
1. Провести полное исследование и построить графики функций:
а) у = 2x3 + 3x2, б) y = 
2. Резервуар, который должен иметь квадратное дно и быть открытым сверху, нужно выложить внутри свинцом. Каковы должны быть размеры резервуара емкостью в 32 л, чтобы выкладка требовала наименьшего количества свинца?
Вариант 3
1. Провести полное исследование и построить графики функций:
а) y = 4x3 – 3x4, б) y = 
2. Требуется устроить прямоугольную площадку так, чтобы с трех сторон она была отгорожена проволочной сеткой длины L, а четвертой стороной примыкала к длинной каменной стене. Каковы должны быть длины сторон прямоугольника, чтобы площадь площадки была наибольшей?
Вариант 4
1. Провести полное исследование и построить графики функций:
а) y = 3x2 – 2x3 – 1, б) y = 
2. Прямо над центром круглой площадки радиуса R нужно повесить фонарь. На какой высоте нужно это сделать, чтобы он наилучшим образом освещал дорожку, которой обведена площадка? (Степень освещения некоторой площадки прямо пропорциональна косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника света).
Вариант 5
1. Провести полное исследование и построить графики функций:
а) y = (x2 – 3)2, б) y = 
2. Закрытая банка данного объема V имеет форму цилиндра. Каково должно быть соотношение радиуса и высоты банки, чтобы на ее изготовление пошло наименьшее количество жести?
Вариант 6
1. Провести полное исследование и построить графики функций:
а) y = x3 +  x4, б) y =
x4, б) y = 
2. Миноносец стоит на якоре в 9 км от ближайшей точки берега; с миноносца надо послать гонца в военный лагерь, расположенный в 15 км, считая по берегу от ближайшей к миноносцу точки берега. Если гонец может делать пешком по 5 км/ч, а на веслах по 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
Вариант 7
1. Провести полное исследование и построить графики функций:
а) y = x5 – 5x, б) y = 
2. Сечение шлюзового канала имеет форму прямоугольника, заканчивающегося полукругом. Периметр сечения равен 45м. При каком радиусе полукруга сечение будет иметь наибольшую площадь?
Вариант 8
1. Провести полное исследование и построить графики функций:
а) y = x3 – 3x2, б) y = 
2. Через точку М(1,2) проведена прямая так, что треугольник, образованный ею с положительными полуосями координат, имеет наименьшую площадь. Составить уравнение этой прямой.
Вариант 9
1. Провести полное исследование и построить графики функций:
а) y = 3x4 – 4x3 + 1, б) y = 
2. Из квадратного жестяного листа со стороной a желают сделать открытый сверху ящик возможно большого объема, вырезая равные квадраты по углам, удаляя их и затем загибая жесть, чтобы образовать бока ящика. Какова должна быть длина стороны вырезаемых квадратов?
Вариант 10
1. Провести полное исследование и построить графики функций:
а) y = -  (x2 – 6)2, б) y =
(x2 – 6)2, б) y = 
2. Открытый жестяной бак с квадратным основанием должен вмещать V литров. При каких размерах бака на его изготовление потребуется наименьшее количество жести?