Класс
Задача 1
В тот момент, когда мимо речной пристани по течению реки проплывает плот, от пристани начинает двигаться вниз по течению моторная лодка, направляясь в деревню, расположенную на расстоянии 𝑠𝑠 = 21 км от пристани (вдоль берега). Лодка приплывает в деревню через 𝑡𝑡 = 45 мин, поворачивает обратно и встречает плот на расстоянии 𝑙𝑙 = 15 км от деревни.
1) Чему равна скорость 𝑢𝑢 течения реки? Ответ выразите в км/ч, округлив до целого числа. (7 баллов)
2) Найдите скорость лодки 𝑣𝑣 относительно воды. Ответ выразите в км/ч, округлив до целого числа. (3 балла)
Возможное решение
В системе отсчёта, связанной с водой, плот стоит, а лодка плывёт туда и обратно со скоростью 𝑣𝑣 относительно воды. Значит, лодка встретит плот через 1,5 часа (она плывет туда 45 мин и обратно 45 мин). За время 2𝑡𝑡 деревня сближается с плотом до расстояния 𝑙𝑙 и проходит путь 𝑠𝑠 − 𝑙𝑙. Скорость течения равна
Скорость лодки:
𝑢𝑢 = 𝑠𝑠−𝑙𝑙 = 4 км/ч.
2𝑡
𝑣𝑣 = 𝑠𝑠−𝑢𝑢𝑡 = 24 км/ч.
𝑡
| Ответы: | 1) | 2) |
Максимум за задачу – 10 баллов.
Задача 2
В деревянном кубике с длиной ребра 𝑎𝑎 = 10 см осталась полость, которую потом полностью залили ртутью и герметично закрыли. Давление, которое стал оказывать кубик на горизонтальный пол, оказалось равным 1440 Па.
1) Чему равна средняя плотность заполненного ртутью кубика? Ответ выразите в кг/м3, округлив до целого числа. (7 баллов)
2) Утонет ли этот кубик с ртутью в воде (да/нет)? (3 балла)
Ускорение свободного падения принять равным 𝑔𝑔 = 10 Н/кг, плотность воды 1000 кг/м3.
Возможное решение
Давление, которое оказывает кубик с ртутью на пол, равно
 𝑝𝑝= �𝑚𝑚к+𝑚𝑚рт �𝑔𝑔
𝑝𝑝= �𝑚𝑚к+𝑚𝑚рт �𝑔𝑔
𝑎2
⟹ 𝜌𝜌 = 𝑚𝑚к+𝑚𝑚рт
𝑎3
= 𝑝𝑝
𝑔𝑔𝑎
= 1440 кг/м3,
где 𝑚𝑚к – масса кубика с полостью, 𝑚𝑚рт – масса ртути, 𝜌𝜌 – средняя плотность заполненного ртутью кубика. Средняя плотность кубика с ртутью больше плотности воды – значит, он утонет.
| Ответы: | 1) | 2) |
| да |
Максимум за задачу – 10 баллов.
Задача 3
Массивный неоднородный стержень (имеющий разную плотность в разных местах) длиной 𝐿𝐿 = 1 м покоится в горизонтальном положении на двух опорах А и В, как показано на рисунке. Силы реакции со стороны опор равны 𝐹𝐴𝐴 = 3 Н и 𝐹𝐵 = 4 Н. Ускорение свободного падения равно 10 м/с2.
А В
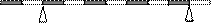
1) Чему равна масса стержня? Ответ выразите в граммах, округлив до целого числа. (4 балла)
2) На каком расстоянии от опоры А находится центр тяжести стержня? Ответ выразите в см, округлив до целого числа. (6 баллов)
Возможное решение
Согласно условию равновесия,
mg = FA + FB.
Откуда
m = FA + FB
 g
g
= 0,7 кг = 700 г.
Сила тяжести, действующая на стержень, равна 𝐹т= 𝐹𝐴𝐴+ 𝐹𝐵= 7 Н. Запишем уравнение моментов для стержня относительно точки A:
7 7 𝐹𝐵


|
𝐿𝐿 = 40 см.
| Ответы: | 1) | 2) |
Максимум за задачу – 10 баллов.
Задача 4
Поплавок массой 7 г плавает в воде, погрузившись на треть своего объёма.
1) Чему равна сила Архимеда, действующая на поплавок? Ускорение свободного падения равно 10 м/с2. Ответ выразите в мН, округлив до целого числа. (4 балла)
2) Какую минимальную силу необходимо приложить к поплавку, чтобы удержать его в полностью погружённом состоянии? (6 баллов)
Возможное решение
В начальном состоянии сила Архимеда равна 1 𝜌𝜌𝑔𝑔𝑔𝑔, где 𝜌𝜌 – плотность
воды, 𝑔𝑔 – объём поплавка. Так как эта сила уравновешивает силу тяжести, действующую на поплавок, значит, 𝑚𝑚𝑔𝑔 = 1 𝜌𝜌𝑔𝑔𝑔𝑔. Условие равновесия
поплавка в конечном состоянии:
𝜌𝜌𝑔𝑔𝑔𝑔 = 𝑚𝑚𝑔𝑔 + 𝐹 ⟹ 𝐹 = 𝜌𝜌𝑔𝑔𝑔𝑔 − 𝑚𝑚𝑔𝑔 = 3𝑚𝑚𝑔𝑔 − 𝑚𝑚𝑔𝑔 = 2𝑚𝑚𝑔𝑔 = 140 мН.
| Ответы: | 1) | 2) |
Максимум за задачу – 10 баллов.