Описание лабораторной установки. Коэффициент пропорциональности определяется по градуировочной кривой термопары

На лабораторной установке (рис.7) тигель 3 с рабочим веществом 4 установлен над нагревателем 2. На штативе 5 укрепле­на термопара 1. Термопара представляет собой два спаянных провод­ника из разных металлов. Если спаи 12 и II имеют разную темпера­туру, то на концах термопары (клеммы 8) возникает термоЭДС Е. Один конец термопары (12) погружен в нагреваемое рабочее вещество (металл), а другой (11) - имеет температуру окружающего воздуха T₁, измеряемую термометром 9. ТермоЭДС прямо пропорциональна разности температур горячего T₂ и холодного T₁ спаев

 

 

Коэффициент пропорциональности определяется по градуировочной кривой термопары (рис. 8). Величина термоЭДС измеряется цифровым вольтметром 10 через равные промежутки времени после нагревания тигля с рабочим веществом, а также при охлаждении ра­бочего вещества. Температура Т₂, вычисляется по формуле T₂ = ∆T + T_1.

 

Порядок выполнения работы

1. Соединить проводниками клеммы 8 термопары со входом цифрового вольтметра. Положить в нагреватель не более четверти таблетки сухого горючего. Включить цифровой вольтметр.

 

2. Зажечь сухое горючее, включить секундомер и производить измерение ЭДС через каждые 10 с.

3. После того как будет отмечено несколько одинаковых значе­ний ЭДС (соответствующих плавлению металла), продолжать измерения, пока температура не начнет устойчиво повышаться. Через 3-4 изме­рения потушить (задуть) сухое горючее.

4. Снять кривую охлаждения. Для этого измерять Е, через каждые 10 с по мере охлаждения металла.

5. По графику градуировки термопары определить разность тем­ператур ∆Т для каждого значения ЭДС при плавлении и кристалли­зации металла.

6. Определить комнатную температуру T₁ и, прибавив ее к зна­чениям ∆T, полученным из графика, найти и записать температуру металла, соответствующую каждому измерению.

7. Построить графики зависимости температуры T металла от времени при плавлении и кристаллизации.

8. По графикам определить среднюю температуру плавления и кристаллизации.

9. По температуре плавления и данным табл.2 идентифицировать рабочее вещество и найти его удельную теплоту плавления.

10. По формуле (39) определить теплоту плавления для дан­ной массы рабочего вещества (m = 85 г) и, используя соотношение (38), вычислить изменение энтропии фазового перехода для слу­чая плавления и кристаллизации.

 

II. Определить погрешности изменения энтропии.

Таблица 2

Металл	Тпл, К	rn, кДж/кг
I. Алюминий	931,1	396,79
2. Висмут		54,4
3. Олово	504,86	61,12
4. Свинец	600,4	20,93
5. Серебро		92,09
6. Сурьма	903,5	101,72
7. Цинк	692,5	111.35
8. Сплав: олово 61 %,
свинец 39 %		45.44
9. Сплав: олово 40 %,
свинец 60 %
10. Сплав: олово 30 %,
свинец 70 %

 

Контрольные вопросы и задания

 

1. Что называется фазовым переходом первого рода, второго рода?

2. Что называется плавлением и кристаллизацией твердых тел.

3. Раскройте сущность физического смысла изменения энтропии при плавлении и кристаллизации твердых тел.

4. Какие системы называют гомогенными и гетерогенными? Что называется фазой в термодинамике?

5. Объясните ход температурной кривой при плавлении и крис­таллизации?

6. Что называется удельной теплотой плавления твердого тела? Как она определяется?

 

7. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ МЕТАЛЛА

 

Цель работы

 

Определить сопротивление не нагретой и нагретой металлической проволоки, ее удлинение при нагревании и коэффициент линейного расширения.

 

Приборы и принадлежности

 

Нихромовая проволока (Ni 90 %, Сr 10 %), источник питания постоянного тока, вольтметр, амперметр, пружина, шкала для измере­ния длины проволоки.

 

Теоретическое введение

 

Опыт показывает, что с повышением температуры происходит расширение твердя тел, называемое тепловым расширением. Для ха­рактеристики этого явления введены коэффициенты линейного и объем­ного расширения. Пусть l₀ - длина тела при температуре 0 ˚С. Удлинение этого тела ∆ l при нагревании его до температуры t°С пропорционально первоначальной длине l₀ и температуре:

 

 

где α - коэффициент линейного расширения, характеризующий относительное удлинение ∆ l/l, происходящее при нагревании тела на 1 К.

Длина тела при температуре t

 

отсюда

 

Тепловое расширение большинства твердых тел весьма незначи­тельно. Поэтому длина l₀ при 0 °С очень мало отличается от дли­ны l при другой температуре t, например комнатной. Поэто­му в выражении коэффициента линейного расширения (41) l₀ можно заменить на l₁, а l - на длину l₂ при температуре t₂, значительно большей, чем t₁:

 

 

Причина расширения твердых тел при нагревании - возрастание амплитуды тепловых колебаний атомов. График зависимости потенци­альной энергии взаимодействия соседних атомов от расстояния между их центрами r приведен на рис. 9. Пунктиром показан уровень полной энергии E взаимного колебания атомов при данной темпе­ратуре. При данной энергии Е расстояние между атомами при теп­ловых колебаниях изменяется от r₁ до r₂. Если r₀<r<r₁ (атомы сближаются), между атомами действуют силы отталкивания. Когда r=r₀, полная энергия равна кинетической энергии теплового колебательного движения. При уменьшении r до r₁ происходит переход кинетической энергии в потенциальную энергию взаимодействия атомов. Далее под действием сил отталкивания атом движется в сто­рону увеличения r. Его кинетическая энергия возрастает, а по­тенциальная - уменьшается. Когда r становится больше r₀, воз­никают силы притяжения между атомами, кинетическая энергия атома уменьшается, а потенциальная увеличивается. В точке r=r₂, пол­ная Е энергия переходит в потенциальную. Далее под действием сил притяжения атомы начинают сближаться И весь процесс колебаний атома между точками r₁ и r₂ повторяется.

 

 

Как видно из рис.9, вследствие несимметричности кривой и(r) среднее расстояние между соседними атомами при данной температуре

 

 

больше, чем r₀, и возрастает с ростом температуры, так как увеличивается полная энергия атома.

 

Описание лабораторной установки и метода измерений.

 

Схема лабораторной установки приведена на рис. 10.

 

 

Нихромовая проволока 1 закреплена между клеммами 2, 3, при­чем клемма 3 соединена с растягивающей пружиной 4. По проволоке течет постоянный ток. Сила тока I измеряется амперметром A, а напряжение U вольтметром V. По закону Джоуля - Ленца в проводнике, по которому течет ток, выделяется тепло

 

 

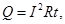
зависящее от времени его прохождения t, сопротивления проводни­ка R и силы тока I. Проводник нагревается, сопротивление металла увеличивается с ростом температуры по закону

 

 

где R₁ - сопротивление проводника при комнатной температуре t₁ °С;

R₂ - его сопротивление при нагревании до температуры t₂ °С;

β - температурный коэффициент сопротивления нихромовой проволоки,

Из соотношения (43) можно определить разность температур

 

 

зная сопротивления R₁ и R₂.

Сопротивление R₁, определяется по формуле

 

 

где ρ - удельное сопротивление нихрома при t₁ = 20 °С; ;

l₁ - длина проволоки при комнатной температуре, м, l₁ = 0,34; d - ее диаметр, мм, d = 0,4.

Сопротивление проволоки R₂ при температуре t₂ опреде­ляется по закону Ома для участка цепи

 

 

Удлинение проволоки при нагревании измеряется по шкале 5.