Тема: Линейные активные цепи и прохождение сигналов через них
Работу выполнил студент
группы ЗРЭ-22-17
Митрофанов С.Л.
Проверил преподаватель
Михайлов А.Л.
Чебоксары 2021
СОДЕРЖАНИЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ………….........................................................................3
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.............................................................................................5
2. ПРАКТИЧЕКОЕ ЗАДАНИЕ….………………………………………………………..11
ЗАДАНИЕ 2.1. Спектральный анализ сигналов…………………………………..........11
ЗАДАНИЕ 2.2. Расчет частотных характеристик цепи...................................................17
ЗАДАНИЕ 2.3. Воздействие импульсных сигналов на апериодические цепи..............23
Список литературы...............................................................................................................26
Методические указания
Задание 1. Спектральный анализ сигналов
На рис. 1 представлен сигнал, имеющий следующие параметры: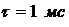 
, 
, 
.
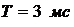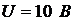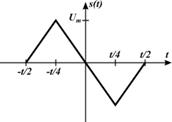
Рис. 1 Исходный сигнал для задания 1
Требуется:
1) определить спектральную плотность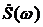 
сигнала 
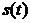. Построить спектральные диаграммы модуля 
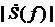и фазы 
, диаграмму энергетического спектра 
;
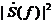2) найти ширину «лепестка» спектра сигнал; и найти ширину спектра одиночного импульса входящего в состав сигнала;
3) рассчитать коэффициенты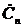 
и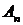 
комплексного и тригонометрического ряда Фурье для периодического сигнала 
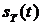, полученного путем повторения заданного сигнала 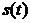с периодом повторения 
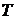. Построить соответствующие спектральные диаграммы 
, 
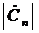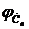и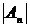 
, 
;
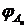4) вычислить энергию сигнал. Построить график автокорреляционной функции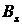 
.
Задание 2.Расчет частотных характеристик цепи
На рис. 2 показана схема активной линейной цепи. В качестве активных элементов использованы идеальные операционные усилители (DA1, DA2), имеющие на всех частотах постоянный коэффициент усиления (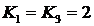
).
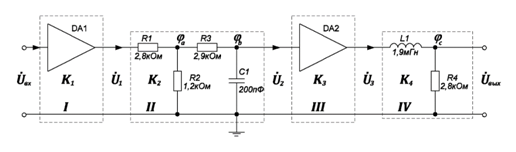
Рис. 2 Исходная цепь для задания 2
Требуется:
1) Определить выражение для комплексной передаточной функции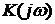 
;
2) Построить графики АЧХ (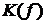
) и ФЧХ (
);
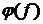3) Определить полосу пропускания цепи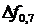 
;
4) Найти в аналитическом виде импульсную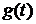 
и переходную характеристики 
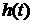. По уровню 0,1 от максимального значения аналитически или графически определить длительность переходных процессов 
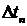. Рассчитать соотношение неопределенностей 
.
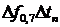Задание 3. Воздействие импульсных сигналов на апериодические цепи
На рис. 3 приведена исходная цепь, требуется определить:
1) передаточную функцию цепи и построить АЧХ и ФЧХ;
2) реакцию цепи на входное воздействие (рис. 4), построив график.
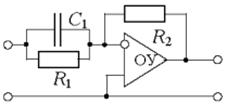
Рис. 3 Исходная цепь для задания 3
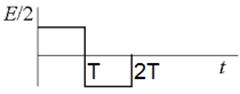
Рис. 4 Исходный сигнал для задания 3
Решение найти в аналитическом виде.
Теоретическая часть
Спектральный анализ детерминированных сигналов. Ряд Фурье
Детерминированным называют любой сигнал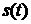 
, мгновенное значение которого можно точно предсказать в любой момент времени.
Сигнал называется четным, если выполняется условие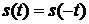 
.
Сигнал называется нечетным, если выполняется условие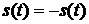 
.
Сигнал называется периодическим, если выполняется условие
, 
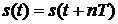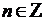, где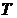 
– период повторения сигнала.
Периодический сигнал можно разложить в ряд Фурье, причем возможны три формы записи:
1) Тригонометрическая. Вещественный сигнал представляется в ви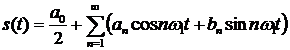де:
, где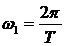 
.
Коэффициенты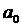 
, 
, 
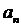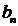вычисляется по следующим формулам:
, 
, 
.
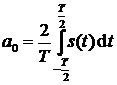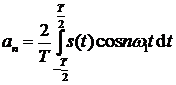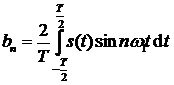В случае если сигнал 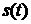четный, то в ряде Фурье отсутствуют слагаемые с коэффициентами 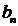. В случае же если, сигнал нечетный, то в ряде Фурье присутствуют слагаемые только с коэффициентами 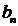. Коэффициент 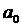представляет собой удвоенное среднее значение сигнала, на интервале 
.
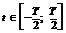2) Вещественная. Введем следующие обозначения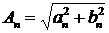 
, 
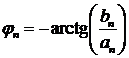. Тогда 
, 
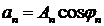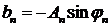. Подставив эти значение в тригонометрический ряд Фурье, придем к вещественной форме ряда Фурье:
.
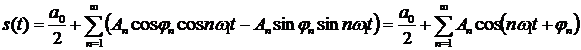Если сигнал 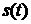четный то 
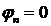, если нечетный то 
.
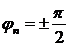3) Комплексная. Использую соотношение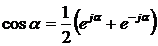 
, получим
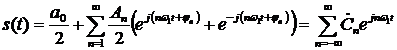, где 
.
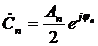Полученное выражение называется рядом Фурье в комплексной форме. Также можно вычислить коэффициенты комплексного ряда Фурье по следующей формуле:
.
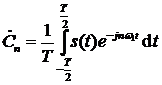Если сигнал 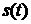четный, то коэффициенты 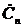будут чисто вещественными. Если сигнал 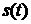нечетный, то коэффициенты 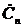будут чисто мнимыми.
Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром, а совокупность их фаз – фазовым спектром.
Связь между коэффициентами ряда Фурье в вещественной и комплексной форме
, 
, 
.
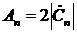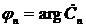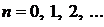Преобразование Фурье
Преобразование Фурье является инструментом спектрального анализа непериодических сигналов. При спектральном анализе непериодических сигналов формула для расчета коэффициентов комплексного ряда Фурье модифицируется следующим образом:
· частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть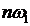 
заменяется на 
);
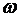· удаляется множитель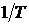 
;
· результатом вычисления вместо нумерованных коэффициентов ряда Фурье 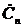является функция частоты 
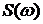– спектральная плотность сигнала.
В результате этих модификаций формула коэффициентов комплексного ряда Фурье превращается в формулу прямого преобразования Фурье:
.
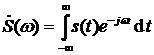В формуле самого комплексного ряда Фурье суммирование, естественно, заменяется интегрированием (и, кроме того, перед интегралом появляется деление на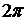 
). Получающееся выражение называется обратным преобразованием Фурье:
.
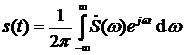Между преобразованием Фурье и коэффициентами комплексного ряда Фурье имеется связь, а именно
.
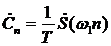