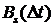1) Линейность. Если 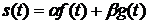 , то
, то 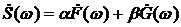 ;
;
2) Задержка. Если 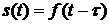 , то
, то 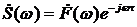 ;
;
3) Изменение масштаба времени. Если 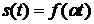 , то
, то 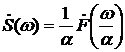 . Отсюда следует важный вывод, что при уменьшении длительности сигнала (
. Отсюда следует важный вывод, что при уменьшении длительности сигнала (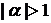 ) спектр сигнала расширяется, а амплитуды гармонических составляющих уменьшаются. И наоборот, если длительность сигнала увеличивается (
) спектр сигнала расширяется, а амплитуды гармонических составляющих уменьшаются. И наоборот, если длительность сигнала увеличивается (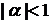 ), то спектр сигнала сужается и увеличиваются амплитуды гармонических составляющих;
), то спектр сигнала сужается и увеличиваются амплитуды гармонических составляющих;
4) Дифференцирование. Если 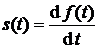 , то
, то 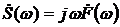 . Мнимое число
. Мнимое число 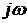 называют оператором дифференцирования в частотной области;
называют оператором дифференцирования в частотной области;
5) Интегрирование. Если 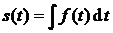 , то
, то 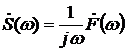 . Мнимое число
. Мнимое число 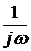 называют оператором интегрирования в частотной области;
называют оператором интегрирования в частотной области;
6) Свертка. Если 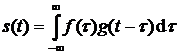 , то
, то 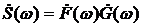 ;
;
7) Произведение. Если 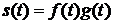 , то
, то 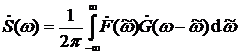 ;
;
Рассмотрим пример использования описанных выше свойств для вычисления спектральной плотности.
Пример. Найти спектральную плотность сигнала приведенного на рис. 5а.
Решение. Как следует из рисунка, данный сигнал описывается следующей функцией:
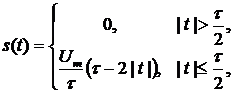
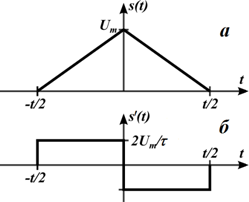
Рис. 5 Исходный сигнал (а) и его производная (б)
производная же этого сигнала (рис. 5б)
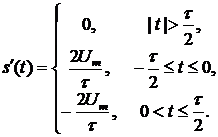
Найдем спектральную плотность производной сигнала 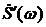 :
:
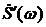
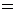
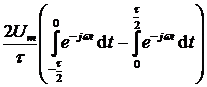
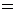
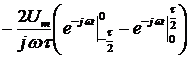
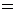
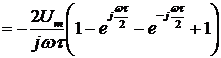
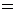
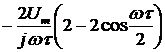
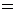
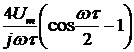 .
.
Искомая спектральная плотность 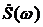 будет равна
будет равна
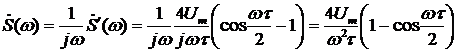 .
.
Автокорреляционная функция
Автокорреляционная функция 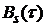 характеризует степень связи (корреляции) сигнала
характеризует степень связи (корреляции) сигнала 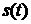 со своей копией сдвинутой на величину
со своей копией сдвинутой на величину 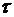 по оси времени и определяется по формуле
по оси времени и определяется по формуле
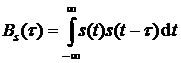 .
.
Свойства:
1) При временном сдвиге равном нулю (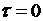 ) значение автокорреляционной функции
) значение автокорреляционной функции 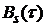 равно энергии сигнала
равно энергии сигнала 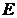 ;
;
2) Автокорреляционная функция четная, т. е. 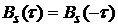 ;
;
3) При любом значении временного сдвига 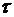 модуль автокорреляционной функции
модуль автокорреляционной функции 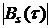 не превосходит энергии сигнала;
не превосходит энергии сигнала;
4) Между автокорреляционной функцией и энергетическим спектром имеется связь:
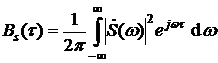 ,
,
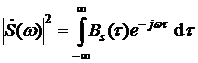 .
.
Линейные цепи
Линейная цепь описывается дифференциальным уравнением с постоянными коэффициентами 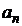 и
и 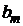 :
:
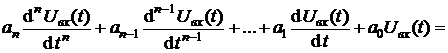
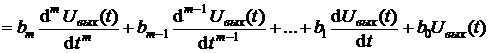 .
.
Перейдя в частотную область, можем записать:
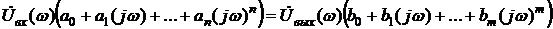 .
.
Передаточная функция 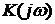 представляет собой отношение комплексных амплитуд выходного
представляет собой отношение комплексных амплитуд выходного 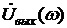 и входного
и входного 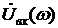 гармонических сигналов заданной частоты
гармонических сигналов заданной частоты 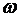 :
:
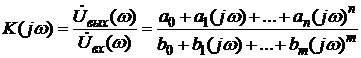 .
.
При обобщении выражения 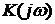 для случая комплексной частоты
для случая комплексной частоты 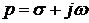 получим операторный коэффициент передачи
получим операторный коэффициент передачи 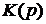
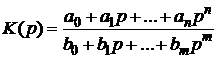 .
.
Импульсная характеристика линейной системы – это отклик системы на единичный импульс 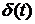 , т. е.
, т. е. 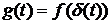 .
.
Переходная характеристика линейной системы – это отклик системы на единичный скачок 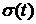 , т. е.
, т. е. 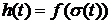 .
.
Между импульсной и переходной характеристикой системы, а также передаточной функцией есть взаимосвязи
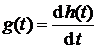 ,
, 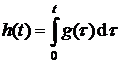 ,
,
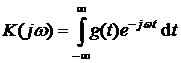 ,
, 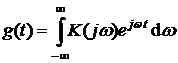 ,
,
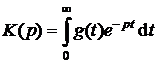 ,
, 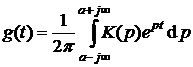 .
.
Из этих формул следует, что если передаточная функция записана в операторной форме, то ее оригиналом является импульсная характеристика.
Передаточную функцию можно представить в виде:
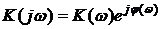 ,
,
где 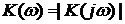 – амплитудно-частотная характеристика (АЧХ),
– амплитудно-частотная характеристика (АЧХ), 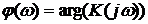 – фазово-частотная характеристика (ФЧХ).
– фазово-частотная характеристика (ФЧХ).
Если линейная цепь состоит из нескольких звеньев с передаточными функциями 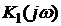 ,
, 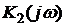 ,…,
,…, 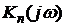 , то передаточная функция всей системы
, то передаточная функция всей системы 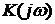 представляет собой произведение передаточных функций отдельных звеньев:
представляет собой произведение передаточных функций отдельных звеньев:
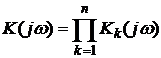 .
.
Для определения выходного сигнала 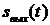 при прохождении сигнала
при прохождении сигнала 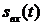 через линейную цепь используют несколько способов:
через линейную цепь используют несколько способов:
1) Метод интеграла наложения. Сигнал на выходе линейной цепи определяется через свертку входного сигнала и импульсной характеристики
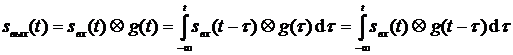 ;
;
2) Спектральный метод. По свойству преобразования Фурье о свертке сигналов, выходная спектральная плотность будет равна
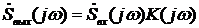 ,
,
используя обратное преобразование Фурье, получим
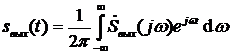 ;
;
3) Операторный метод. При операторном методе вместо преобразования Фурье используют преобразование Лапласа
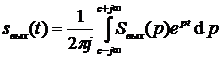 ,
,
где
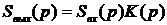 ,
, 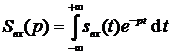 ,
, 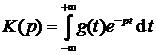 .
.
Для сложных функций 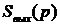 можно перейти от интеграла
можно перейти от интеграла 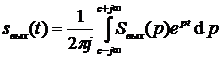 к сумме вычетов, т. е.
к сумме вычетов, т. е.
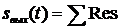 ,
,
где 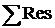 – сумма вычетов в полюсах подынтегральной функции.
– сумма вычетов в полюсах подынтегральной функции.
Практическая часть.
Спектральный анализ
1) Вычислим спектральную плотность сигнала 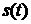 приведенного на рис. 6.
приведенного на рис. 6.
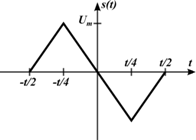
Рис. 6 Исходный сигнал
В теоретической части был рассмотрен пример симметричного треугольного импульса, его спектральная плотность 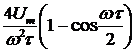 , а длительность составляла
, а длительность составляла 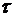 . Сигнал
. Сигнал 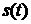 состоит из двух таких масштабированных и смещенных треугольных импульсов. Найдем спектральную плотность
состоит из двух таких масштабированных и смещенных треугольных импульсов. Найдем спектральную плотность 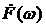 треугольного симметричного импульса с длительностью
треугольного симметричного импульса с длительностью 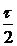 :
:
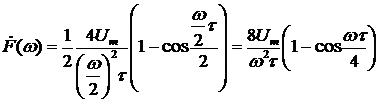 .
.
Отсюда следует, что спектральная плотность 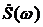 будет равна:
будет равна:
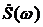
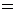
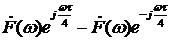
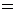
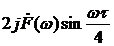
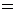
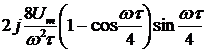
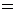
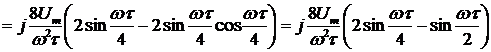 .
.
Так как сигнал 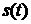 является нечетной функцией, то на нулевой частоте спектральная плотность равна нулю.
является нечетной функцией, то на нулевой частоте спектральная плотность равна нулю.
2) Найдем нули спектральной плотности 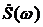 :
:
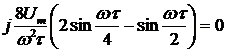 ,
,
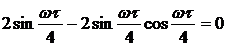 ,
,
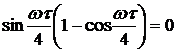 ,
,
так как 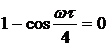 при
при 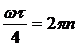 , а
, а 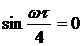 , при
, при 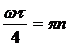 , где
, где 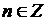 . Таким образом, переходя к частоте
. Таким образом, переходя к частоте 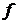 получим
получим
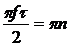 , или
, или
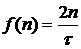 ,
,
ширина главного лепестка 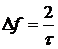 .
.
Спектральная плотность 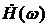 левой половины сигнала
левой половины сигнала 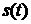 (считаем, что правая половина сигнала равна нулю):
(считаем, что правая половина сигнала равна нулю):
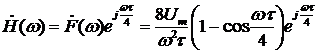 ,
,
Спектральная плотность 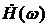 , будет содержать отличное от нуля значение на нулевой частоте. Чтобы вычислить это значение, перейдем к пределу
, будет содержать отличное от нуля значение на нулевой частоте. Чтобы вычислить это значение, перейдем к пределу
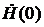
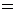
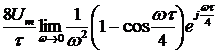
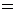
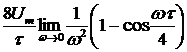
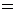
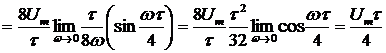 , т. е. площадь сигнала
, т. е. площадь сигнала 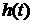 .
.
найдем нули спектральной плотности 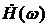 :
:
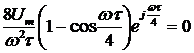 , т. е. при условии
, т. е. при условии
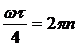 , где
, где 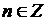 и
и 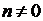 , переходя к частоте
, переходя к частоте 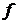 ,
,
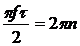 ,
, 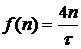 ,
,
ширина главного лепестка 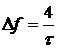 .
.
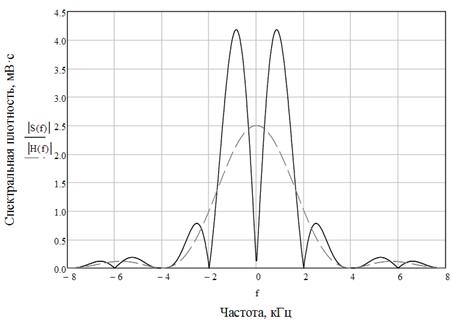
Рис. 7. Модули спектральной плотности 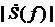 и
и 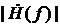
Таким образом, ширина спектра половины сигнала 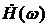 в два раза больше ширины спектра
в два раза больше ширины спектра 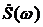 , а амплитуда примерно в два раза меньше. Что подтверждается полученными формулами, также это видно графически на рис. 7.
, а амплитуда примерно в два раза меньше. Что подтверждается полученными формулами, также это видно графически на рис. 7.
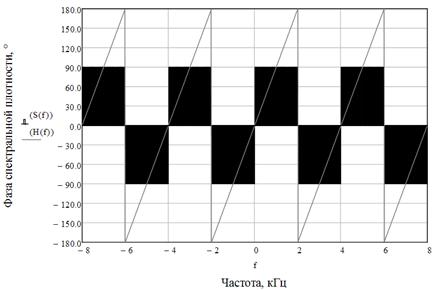
Рис. 8. Фаза спектральной плотности 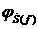 и
и 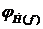
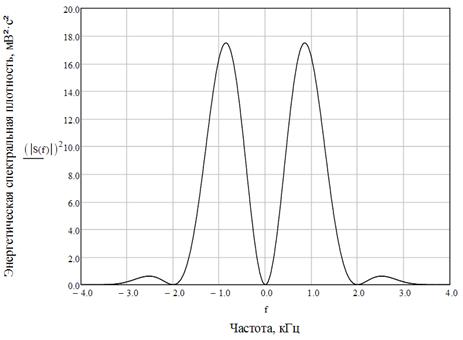
Рис. 9. Энергия спектральной плотности 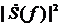
3) Вычислим коэффициенты комплексного ряда Фурье 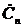 сигнала
сигнала 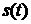 , период сигнала
, период сигнала 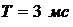 (рис. 10, рис. 11):
(рис. 10, рис. 11):
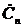
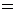
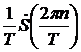
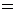
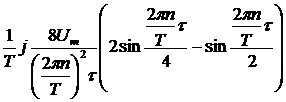
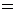
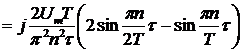 .
.
Для вещественного ряда Фурье получим (рис. 12, рис. 13):
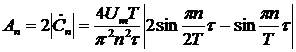 ,
, 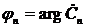 .
.
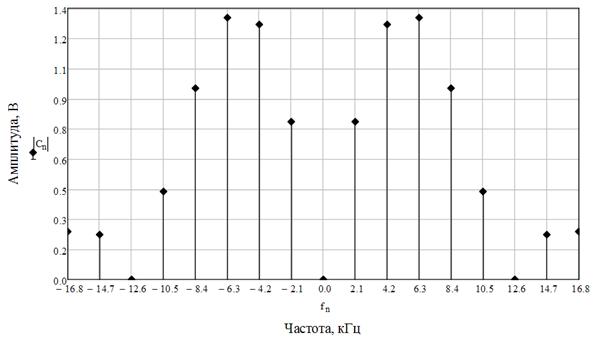
Рис. 10 Амплитудный спектр 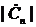
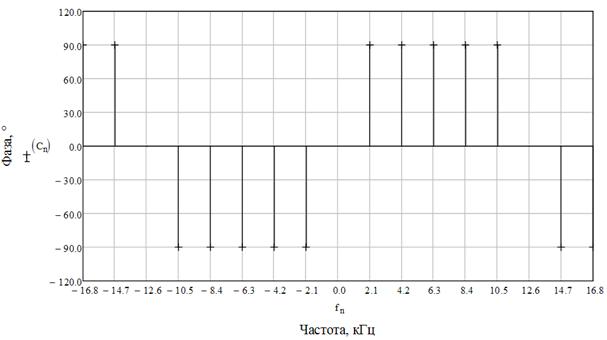
Рис. 11 Фазовый спектр 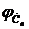
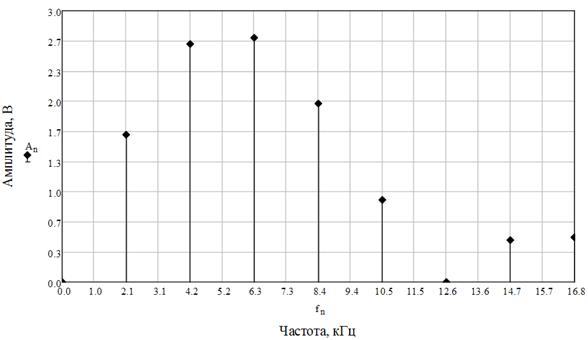
Рис. 12 Амплитудный спектр 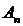
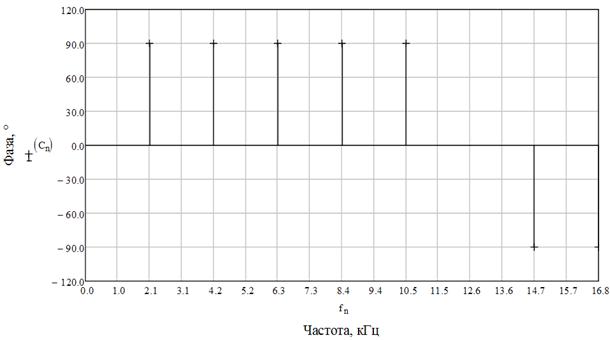
Рис. 13 Фазовый спектр 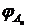
4) Вычислим энергию сигнала:
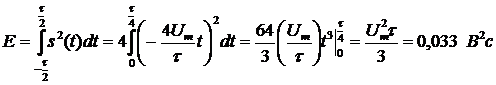 ,
,
такой же результат был получен при вычислении энергии через квадрат спектральной плотности
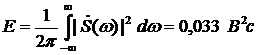 ,
,
этот результат получен в программе MathCad.
Автокорреляционная функция (рис. 14) вычисляется по формуле:
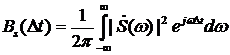 ,
,
где 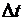 – время сдвига.
– время сдвига.
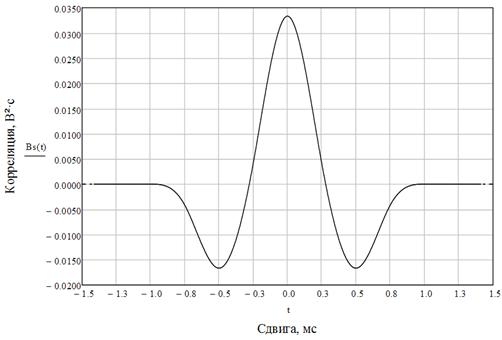
Рис. 14 Автокорреляционная функция