Теоретическое описание акустических волн на поверхности твердого тела.

Волны Рэлея.

Как уже отмечалось ранее на поверхности твердого тела могут существовать волны различных типов. Волна Рэлея на свободной поверхности состоит из продольной волны сжатия-растяжения и поперечной волны сдвига. Вторым важным типом поверхностных акустических волн является волна Гуляева-Блюштейна (ВГБ), которая так же может существовать на свободной поверхности твердого тела, но в отличие от рэлеевской волны существование ВГБ возможно только на определенных срезах и в определенных направлениях пьезоэлектрических кристаллов. В системе полупространство-слой чисто механическое возмущение границы приводит к образованию сдвиговой волны Лява. Волны Лява находят некоторое применение на практике в лабораторных исследованиях. В теории эти волны часто используют в качестве простейшей модели поверхностных волн, так как расчеты для волн Лява существенно проще, чем для волн Рэлея. Так же следует отметить случай, когда на поверхности имеются неровности. Приповерхностная жесткость в такой системе меньше за счет наличия канавок, что приводит к образованию сдвиговых поверхностных волн (СПВ). Скорость волны в приповерхностной области уменьшается, так как волна как бы обегает выступы, проходя при этом больший путь. В данной работе проводится исследование распространения рэлеевской волны по поверхности твердого тела, которая имеет как случайные неоднородности (шероховатая поверхность) так и искусственные дефекты представляющие из себя наноразмерную периодическую структуру.

 

 

Z

	Рис.1. Система координат к вопросу о распространении рэлеевской волны.

 

 

При описании волн Рэлея [7], распространяющихся вдоль границы изотропного упругого полупространства (рис.3), смещение удобно выражать через скалярный j и векторный потенциалы:

 

(1)

 

причем такое представление возможно при любой пространственной структуре волновых полей и соответствует разделению волны на волну сжатия (j) и волну сдвига (). Уравнения для j и независимы и записываются в виде:

 

, , (2)

 

где D-оператор Лапласа, и -скорости продольной и поперечной акустических волн соответственно. При распространении волны вдоль оси x (рис.1) и векторе смещения, лежащем в плоскости xz, векторный потенциал имеет одну компоненту , отличную от нуля. При этом смещения и даются формулами:

 

, . (3)

 

Используя эти выражения и закон Гука для изотропного тела, можно записать отличные от нуля компоненты тензора напряжений:

 

,

,

, (4)

,

 

где и -постоянные Ламе, причем ,

( -плотность упругого тела).

Решения уравнений (2), описывающие поверхностную акустическую волну, имеют вид:

 

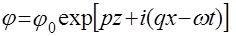, (5)

,

 

где и - частота и волновое число волны, и - амплитуды двух компонент волны, и 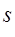-коэффициенты, описывающие спадание волн сжатия и сдвига в глубь поверхности.

Из уравнений движения (2) следует, что

 

, , > ,

 

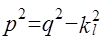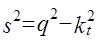где , - волновые числа продольной и сдвиговой объемных волн.

На свободной границе полупространства z=0 должны выполняться условия отсутствия напряжений 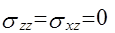. Из выражений (4) при этом следует:

 

, (6)

.

 

Выражение в квадратных скобках преобразуется к виду , после чего система (6) записывается в виде:

 

, (7)

.

 

Из условия существования ненулевых решений этой линейной системы уравнений получается уравнение Рэлея

 

. (8)

 

Вводя скорость волны Рэлея , легко видеть, что не зависит от частоты, т.е. волны Рэлея в классическом упругом теле

бездисперсны и отношение определяется отношением , т.е. зависит только от коэффициента Пуассона .

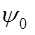Амплитуды потенциалов и линейно связаны уравнениями (7), поэтому решения (5) можно представить в виде:

 

, (9)

.

 

Значения смещений и вычисляются по формулам (3); в частности, для амплитуды смещения на поверхности имеем:

 

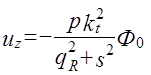, (10)

 

соответственно 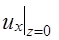дается формулой:

 

. (11)

 

Из этих формул видно, что смещение частиц среды в волне Рэлея происходит по эллипсам, причем на «гребнях» волны частицы движутся в направлении, противоположном направлению распространения волны.

Поток энергии в волне Рэлея в расчете на единицу ширины акустического пучка с использованием формул (9) можно представить формулой:

 

, (12)

 

где поток энергии представлен в Вт/см, частота в ГГц, плотность в г/см , амплитуда в , 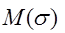- функция коэффициента Пуассона, скорость в см/с.

Приведенные соотношения позволяют рассчитать все основные характеристики волны Рэлея в изотропном твердом теле.

 

Распространение ПАВ на шероховатых поверхностях и в мелкомасштабных периодических структурах.

Далее перейдем к рассмотрению распространения волны Рэлея на шероховатой поверхности. Основными явлениями на таких поверхностях являются затухание и дисперсия ПАВ обусловленные взаимодействием с двумерными и трехмерными шероховатостями. Рассмотрим теоретический подход к расчету затухания и дисперсии.

Пусть на выступ или выемку, находящиеся на гладкой поверхности, падает поверхностная волна, характеризуемая амплитудами смещений . В результате взаимодействия с неоднородностью полное поле в упругой среде будет отличаться от поля падающей волны, принимая значение .Получим интегральное уравнение, определяющее рассеянное поле . Полное поле в ограниченной упругой среде вдали от источников должно удовлетворять уравнению движения:

 

, (13)

 

замыкаемому линеаризованным уравнением состояния:

 

, (14)

 

где - плотность среды, - компоненты тензора упругих напряжений, - компоненты линеаризованного тензора деформаций, 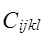- упругие постоянные;

и однородным граничным условием на свободной поверхности:

, (15)

 

где - вектор единичной нормали к поверхности.

Тогда для описания рассеяния волны на неоднородностях поверхности используется интегральное уравнение:

 

, (16)

 

где точка находится внутри контура С, а точка лежит на С, - тензор Грина для смещений, П – скалярный дифференциальный оператор.

Физический смысл данного уравнения состоит в том, что оно описывает рассеянное поле, возникающее в результате действия на поверхность С₂, С₁^/, С₃ (рис.2) ненулевых напряжений, обусловленных наличием препятствий.

Ограничиваясь рассмотрением только изотропных твердых тел, для которых , перейдем к уравнению в потенциалах 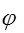и .

Если рассматривать смещения только в плоскости xz, то векторный потенциал будет иметь лишь одну компоненту и соответствующее уравнение для вектора Ф примет вид:

 

, (17)

 

индекс m принимает значения x и z, - оператор возмущений.

Для малых препятствий наиболее простым методом решения данного уравнения является итерационный метод, в котором за нулевое приближение к решению выбирается поле падающей волны . Последующие приближения получаются подстановкой низших приближений в интеграл уравнения. В результате решение представляется в виде итерационного ряда (борновский ряд)

, (18)

 

Условие применимости борновского приближения накладывает ограничения на размеры и форму препятствий. В данном случае оно имеет вид:

 

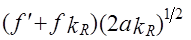<< 1, (19)

 

где функция описывающая дефект на плоской поверхности, - максимальная глубина дефекта, - производная по функции описывающей профиль дефекта, , , 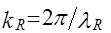- длина рэлеевской волны.

Можно произвести соответствующие оценки для фазового сдвига, связанного с увеличением пути, проходимого рэлеевской волной при огибании ею искривленной поверхности препятствия.

		б)
		а)
		Рис.2.

 

 

Если функция, описывающая неровность имеет вид при и равна нулю при 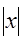> ,то сдвиг фазы рэлеевской волны DQ оценивается формулой:

 

, (20)

 

при этом величину 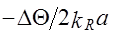можно интерпретировать как кажущееся относительное замедление фазовой скорости волны относительно плоской поверхности ,

 

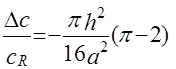. (21)

 

Аналогичные оценки для треугольного препятствия:

. (22)

 

Для того чтобы рассчитать обусловленное шероховатостью затухание рэлеевской волны в борновском приближении, достаточно предположить, что участок шероховатой поверхности ограничен (имеет размеры ) и относительно мал, так что вызываемое им рассеяние может рассматриваться как слабое. Относя полную мощность акустических волн 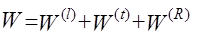, рассеянных участком поверхности площадью , в объемные продольные, поперечные и рэлеевские волны, соответственно; к мощности падающей волны 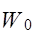, проходящей через указанный участок ( ~ 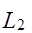), в соответствии с законом сохранения энергии получим следующее выражение для пространственного коэффициента затухания по мощности: . Поскольку 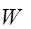~ , а ~ , то очевидно, что не зависит от размеров шероховатого участка. Коэффициент затухания по амплитуде при этом определяется как .

Следует отдельно рассмотреть распространение ПАВ вдоль поверхности, на которой имеются периодические системы неоднородностей в виде, например вытравленных мелких канавок, полосок металла, штырьков и т. п. Такие периодические структуры, расположенные на пути распространения волны, являются основой ряда устройств на ПАВ. Дело в том, что для получения требуемых характеристик устройств необходимо иметь возможность управлять распространением волны: отражать волну с малыми потерями, изменять направление распространения волн, рассеивать волны и т. д. Эти операции, как правило невыполнимы при помощи единичного (локального) рассеивающего элемента и только большое число периодически (или квазипериодически) расположенных возмущений на поверхности позволяет реализовать требуемое управление распространением ПАВ. При этом каждый отдельный элемент может мало влиять на распространение волны, но совокупное их действие оказывается значительным.

Характер рассеяния ПАВ на периодически расположенных системах неоднородностей определяется интерференцией волн, рассеянных на отдельных элементах системы, и, значит существенно зависит от соотношения между периодом структуры и длиной волны. В рамках борновского приближения можно считать, что падающая на структуру волна в области расположения неоднородностей не удовлетворяет граничным условиям, и в этих областях возникают напряжения, порождающие рассеянные волновые поля. Эти сторонние напряжения можно представить в виде набора гармоник с волновыми числами ( - волновое число падающей волны, - волновое число периодической структуры, -период структуры, -волновое число гармоник напряжений, создаваемых на поверхности, (). Если одна из гармоник поверхностных напряжений имеет волновое число, равное или близкое к волновому числу одной из собственных волн системы, происходит интенсивное (резонансное) возбуждение соответствующей волны. Пусть длина волны больше удвоенного периода структуры ( [КР1] > , < ). В этом случае поверхностные напряжения расположены слишком часто (или, что то же самое, волновые числа , и т.д. слишком велики по модулю) и не могут возбуждать волн в системе. Таким образом, при распространении ПАВ по мелкомасштабной ( << ) периодической системе неоднородностей рассеянных волн не возникает. Гармоники напряжений с волновыми числами 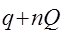вызывают приповерхностные колебания, амплитуда которых много меньше амплитуды ПАВ, если возмущение поверхности мало. Учет этих колебаний приводит лишь к небольшому изменению скорости волны Рэлея. При уменьшении длины волны первая пространственная гармоника поверхностных напряжений совпадает по модулю с волновым числом ПАВ, бегущей в противоположном направлении: , . При этом интенсивно генерируется отраженная волна. Эффект можно описать и как сложение в фазе волн, отраженных отдельными канавками. Действительно, из следует, что . Поэтому падающая волна, проходя расстояние между канавками, меняет фазу на , и отраженная от канавки волна, проходя в обратном направлении расстояние , оказывается в фазе с волной, отраженной от предыдущей канавки.