Классификация звеньев. Простейшие звенья: дифференциальные уравнения, передаточные функции, временные и частотные характеристики, примеры. Звенья первого порядка: дифференциальные уравнения, передаточные функции, временные и частотные характеристики, примеры. Звенья второго порядка: дифференциальные уравнения, передаточные функции, временные и частотные характеристики, примеры. Неминимально-фазовые устойчивые и неустойчивые звенья, передаточные функции, временные и частотные характеристики, примеры
Все элементы системы независимо от их конструктивного исполнения и назначения по своим динамическим свойствам можно подразделить на ограниченное число типовых динамических звеньев. Под типовым динамическим звеном понимают элемент системы направленного действия, описываемый в динамике дифференциальным или алгебраическим уравнением не выше второго порядка. Классифицируют звенья по виду уравнения динамики.
Все звенья можно разделить на два типа: минимально-фазовые и неминимально-фазовые.
Звено является неминимально-фазовым, если его передаточная функция имеет положительные нули или полюса, у таких звеньев фазовая характеристика  не соответствует дифференциальному уравнению. Для минимально-фазовых звеньев фазочастотная характеристика однозначно определяется амплитудно-частотной характеристикой.
не соответствует дифференциальному уравнению. Для минимально-фазовых звеньев фазочастотная характеристика однозначно определяется амплитудно-частотной характеристикой.
Динамические звенья могут быть:
- устойчивыми – если после приложения и снятия воздействия его выходная переменная стремится к значению до момента приложения воздействия (т.е. возвращается в исходное состояние);
- нейтральными (астатическими), если при ступенчатом воздействии выходная переменная изменяется с постоянной скоростью (астатизм первого порядка) или постоянным ускорением (астатизм второго порядка), а после приложения и снятия воздействия приходит в новое устойчивое состояние;
- неустойчивые, если выходная переменная после приложения и снятия возмущения изменяется, не приходя к некоторому устойчивому состоянию.
По типу уравнений динамики минимально-фазовые звенья можно классифицировать следующим образом (таблица 3.1).
Таблица 3.1 – Передаточные функции основных типовых динамических звеньев
| № | Передаточная функция | Название | |

| Усилитель (безынерционное звено) | ||

| Идеальное интегрирующее звено | ||

| Инерционное (апериодическое 1-го порядка) звено | ||

| Реальное интегрирующее звено | ||

| Изодромное звено | ||

| Форсирующее звено | ||

| Идеальное дифференцирующее звено | ||

| Реальное дифференцирующее звено | ||

| Инерционно-форсирующее звено | ||

| при 

| Апериодичское звено 2-го порядка | |
при 
| Колебательное звено | ||
при 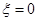

| Консервативное звено | ||

| Звено запаздывания |
Рассмотрим основные типовые звенья, их уравнения динамики, передаточные функции и характеристики.


Безынерционное звено
Выходной сигнал этого звена по форме повторяет входной сигнал. Уравнение динамики:
 ,
,
где K – коэффициент усиления.
Уравнение звена в изображениях:
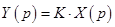 .
.
Передаточная функция:
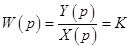 .
.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.

| 
|
| Рисунок 3.1 – Переходная характеристика безынерционного звена | Рисунок 3.2 – Импульсная переходная характеристика безынерционного звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой точку на вещественной оси, отстоящую на расстояние K от начала координат;
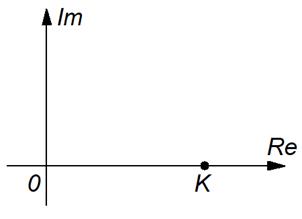
Рисунок 3.3 – АФЧХ безынерционного звена
е)  .
.

Рисунок 3.4 – ЛАЧХ и ФЧХ безынерционного звена
Звено устойчивое.
Примеры безынерционного звена:
– делитель напряжения на двух резисторах R 1 и R 2 (рисунок 3.5 а):
 ;
;
– усилитель на операционном усилителе (рисунок 3.5 б):
 ;
;
– редуктор (рисунок 3.5 в). Входной сигнал – вращающий момент M (t), выходной – частота вращения ω (t):
 ,
,
где  – угловые скорости вращения выходного и входного валов редуктора;
– угловые скорости вращения выходного и входного валов редуктора;  – передаточное число редуктора.
– передаточное число редуктора.

Рисунок 3.5 – Примеры безынерционного звена

Идеальное интегрирующее звено
Выходной сигнал этого звена равен интегралу от входного, уравнение динамики имеет следующий вид:
 ,
,
где  – постоянная интегрирования.
– постоянная интегрирования.
Уравнение звена в изображениях:
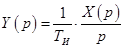 .
.
Передаточная функция:
 .
.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.

| 
|
| Рисунок 3.6 – Переходная характеристика идеального интегрирующего звена | Рисунок 3.7 – Импульсная переходная характеристика идеального интегрирующего звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой отрицательный отрезок мнимой оси;

Рисунок 3.8 – АФЧХ идеального интегрирующего звена
е)  .
.

Рисунок 3.9 – ЛАЧХ и ФЧХ идеального интегрирующего звена
Звено нейтральное.
Примеры идеального интегрирующего звена:
– идеальный конденсатор емкостью С (рисунок 3.10 а), если выходным сигналом является напряжение на конденсаторе UC (t), а входным – ток заряда i (t):
 ;
;
– бассейн с наполняющей его трубой (рисунок 3.10 б) с площадью дна S. Входной сигнал – подача воды Q (t), выходной – уровень воды H (t):
 ;
;
– механическая часть электропривода (рисунок 3.10 в). Входной сигнал – вращающий момент M (t), выходной – угловая частота вращения ω (t):
 ,
,
где J – момент инерции вращающегося тела;
– интегратор на операционном усилителе (рисунок 3.10 г):
 .
.

Рисунок 3.10 – Примеры идеального интегрирующего звена


Идеальное дифференцирующее звено
Выходной сигнал этого звена пропорционален скорости изменения входного сигнала. Уравнение динамики:
 .
.
Уравнение звена в изображениях:
 .
.
Передаточная функция:
 .
.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 – два импульса противоположной полярности.
– два импульса противоположной полярности.

| 
|
| Рисунок 3.11 – Переходная характеристика идеального дифференцирующего звена | Рисунок 3.12 – Импульсная переходная характеристика идеального дифференцирующего звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой положительный отрезок мнимой оси;

Рисунок 3.13 – АФЧХ идеального дифференцирующего звена
е)  .
.

Рисунок 3.14 – ЛАЧХ и ФЧХ идеального дифференцирующего звена
Звено устойчивое.
Примеры идеального дифференцирующего звена:
– идеальная катушка индуктивности L (рисунок 3.15 а). Входной сигнал – ток через катушку i (t), выходной – на катушке UL (t):
 ;
;
– дифференциатор на операционном усилителе (рисунок 3.15 б):
 ;
;
– вращающая часть электрической машины (рисунок 3.15 в). Входной сигнал – угол поворота α (t), выходной – угловая частота вращения ω (t):
 .
.

Рисунок 3.15 – Примеры идеального дифференцирующего звена

Соединением безынерционных, идеальных дифференцирующих и интегрирующих звеньев можно получить все остальные звенья.
Апериодическое (инерционное) звено первого порядка.
Уравнение динамики:
 ,
,
где T – постоянная времени, характеризующая инерционные свойства звена.
Уравнение звена в изображениях:
 .
.
Передаточная функция:
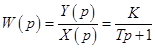 .
.

Рисунок 3.16 – Получение апериодического звена первого порядка
Апериодическое звено первого порядка можно получить, охватив безынерционной обратной связью идеальное интегрирующее звено (рисунок 3.16):
 ;
;
 ,
,  .
.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.

| 
|
| Рисунок 3.17 – Переходная характеристика апериодического звена первого порядка | Рисунок 3.18 – Импульсная переходная характеристика апериодического звена первого порядка |
Установившееся значение переходной характеристики h(∞)=K.
Постоянную времени можно определить по графику h(t) (рисунок 3.8) используя свойство экспоненты – проекция под касательной на линию установившегося значения равна постоянной времени – или определяя время за которое h(t) достигает значение 0,63 h(∞).

Рисунок 3.19 – Определение постоянной времени по переходной характеристике
Комплексный коэффициент передачи:
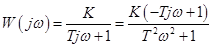 .
.
Частотные характеристики:
а)  ;
;
б)  ;
;
в)  ;
;
г) 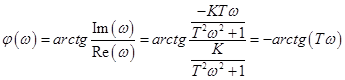 ;
;
д) АФЧХ этого звена представляет собой полуокружность диаметром K, расположенную в четвертом квадранте.

Рисунок 3.20 – АФЧХ апериодического звена первого порядка
е)  .
.
Обычно в ТАУ строят асимптотические ЛАЧХ, которые представляют собой ломаные линии и очень легко рассчитываются. На низких частотах  , второе слагаемое в выражении
, второе слагаемое в выражении  очень мало и его можно не учитывать. При
очень мало и его можно не учитывать. При  второе слагаемое дает значение
второе слагаемое дает значение  . При дальнейшем увеличении частоты вклад второго слагаемого возрастает.
. При дальнейшем увеличении частоты вклад второго слагаемого возрастает.
Поэтому асимптотическую ЛАЧХ строят следующим образом: для частот  по уравнению
по уравнению  – прямая параллельна оси частот; для
– прямая параллельна оси частот; для 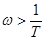 – линия с наклоном -20 дБ/дек. Ошибка на частоте
– линия с наклоном -20 дБ/дек. Ошибка на частоте 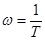 равна 3 дБ, т.е. точная
равна 3 дБ, т.е. точная  на этой частоте проходит ниже на 3 дБ.
на этой частоте проходит ниже на 3 дБ.

Рисунок 3.20 – ЛАЧХ и ФЧХ апериодического звена первого порядка
Звено устойчивое.
Примеры идеального интегрирующего звена:
Дифференциальным уравнением первого порядка описываются переходные процессы в магнитном усилителе (инерционный усилитель), тепловые процессы, процессы растворения и осаждения и другие технологические процессы.





– идеальный конденсатор емкостью С (рисунок 3.10 а), если выходным сигналом является напряжение на конденсаторе UC (t), а входным – ток заряда i (t):
 ;
;
– бассейн с наполняющей его трубой (рисунок 3.10 б) с площадью дна S. Входной сигнал – подача воды Q (t), выходной – уровень воды H (t):
 ;
;
– механическая часть электропривода (рисунок 3.10 в). Входной сигнал – вращающий момент M (t), выходной – угловая частота вращения ω (t):
 ,
,
где J – момент инерции вращающегося тела;
– интегратор на операционном усилителе (рисунок 3.10 г):
 .
.
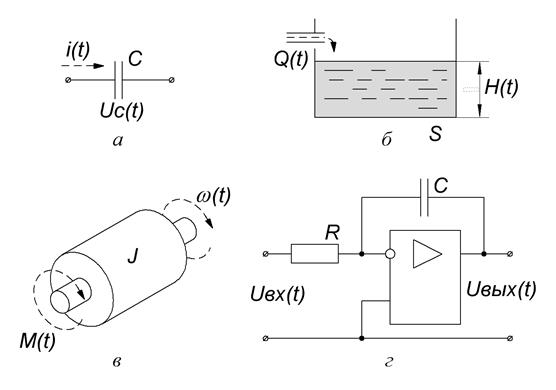
Рисунок 3.21 – Примеры апериодического звена первого порядка
Форсирующее звено
Уравнение динамики:
 .
.
Уравнение звена в изображениях:
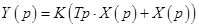 .
.
Передаточная функция:
 .
.

Рисунок 3.22 – Получение форсирующего звена
Форсирующее звено можно получить параллельным соединением идеального дифференцирующего и безынерционного звена (рисунок 3.22):
 ;
;
 ,
,  .
.
Временные характеристики:
а) переходная функция и характеристика:
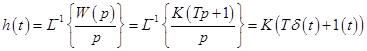 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.

| 
|
| Рисунок 3.23 – Переходная характеристика форсирующего звена | Рисунок 3.24 – Импульсная переходная характеристика форсирующего звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой вертикальную прямую в первом квадранте отстоящую от начала координат на величину K.

Рисунок 3.25 – АФЧХ форсирующего звена
е)  .
.
Асимптотическая ЛАЧХ – ломаная линия, для частот  – прямая параллельная оси частот и отстоящая от нее на расстояние
– прямая параллельная оси частот и отстоящая от нее на расстояние 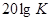 , для
, для  – линия с наклоном +20 дБ/дек.
– линия с наклоном +20 дБ/дек.

Рисунок 3.26 – ЛАЧХ и ФЧХ форсирующего звена
Звено устойчивое
Примеры

Реальное дифференцирующее звено
Уравнение динамики:
 .
.
Уравнение звена в изображениях:
 .
.
Передаточная функция:
 .
.

| 
|
| а | б |
Рисунок 3.28 – Получение реального дифференцирующего звена
Реальное дифференцирующее звено можно получить последовательным соединением идеального дифференцирующего и апериодического звена первого порядка (рисунок 3.28 а) или охватив безынерционное звено идеальной интегрирующей обратной связью (рисунок 3.28 б):
а)  ;
;
 ;
;
б)  ;
;
 ,
,  .
.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.

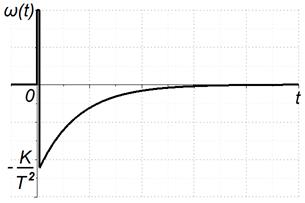
| 
|
| Рисунок 3.29 – Переходная характеристика реального дифференцирующего звена | Рисунок 3.30 – Импульсная переходная характеристика реального дифференцирующего звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а)  ;
;
б) 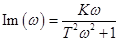 ;
;
в) 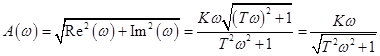 ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой полуокружность диаметром  расположенную в первом квадранте.
расположенную в первом квадранте.

Рисунок 3.31 – АФЧХ реального дифференцирующего звена
е)  .
.
Асимптотическая ЛАЧХ – ломаная линия, для частот  – линия с наклоном +20 дБ/дек, проходящая через точку
– линия с наклоном +20 дБ/дек, проходящая через точку  на оси ординат, для
на оси ординат, для  – прямая параллельная оси частот.
– прямая параллельная оси частот.
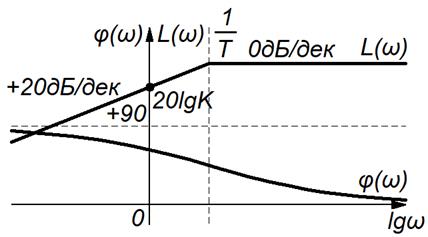
Рисунок 3.32 – ЛАЧХ и ФЧХ реального дифференцирующего звена
Звено устойчивое
Примеры звена:
|
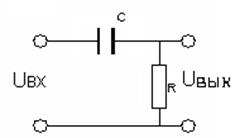
|
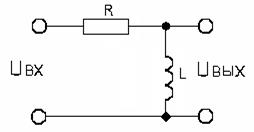




Инерционно-форсирующее звено
Уравнение динамики:
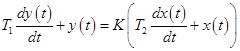 .
.
Уравнение звена в изображениях:
 .
.
Передаточная функция:
 .
.

Рисунок 3.34 – Получение инерционно-форсирующего звена
Инерционно-форсирующее звено можно получить охватив безынерционное звено инерционной обратной связью (рисунок 3.34):
 ;
;
 ,
, 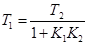 .
.
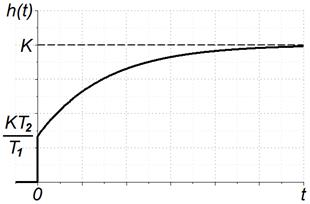
Свойства этого звена зависят от соотношения постоянных времени  и
и  , если
, если  то звено по своим свойствам приближается к инерционному (апериодическому) звену, а если
то звено по своим свойствам приближается к инерционному (апериодическому) звену, а если  – к форсирующему.
– к форсирующему.
Временные характеристики:
а) переходная функция и характеристика:
 ;
;
б) функция веса и импульсная переходная характеристика:
 .
.
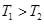
| 
|
| 
|

| 
|
| 
|
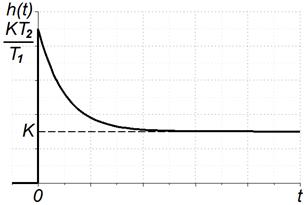
| Рисунок 3.35 – Переходная характеристика инерционно-форсирующего звена | Рисунок 3.36 – Импульсная переходная характеристика инерционно-форсирующего звена |
Комплексный коэффициент передачи:
 .
.
Частотные характеристики:
а) 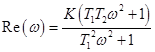 ;
;
б) 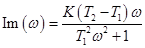 ;
;
в) 

 ;
;
г)  ;
;
д) АФЧХ этого звена представляет собой полуокружность расположенную в первом или четвертом квадранте.
|

|

|

|
Рисунок 3.37 – АФЧХ инерционно-форсирующего звена
е)  .
.

|

|

|
|
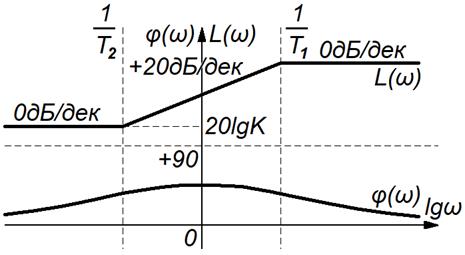
Рисунок 3.38 – ЛАЧХ и ФЧХ инерционно-форсирующего звена
Звено устойчивое