Звено является неминимально-фазовым звеном, если сдвиг по фазе при 0 < ω < ∞ превышает максимально возможное значение для данного типа уравнения динамики.
Звено является неминимально-фазовым, если его W(p) имеет положительный нуль или полюс (корень полинома числителя или знаменателя). Одной и той же АЧХ звена может соответствовать разные ФЧХ.
1. Устойчивое неминимально-фазовое инерционное звено первого порядка
Уравнение:
имеем положительный нуль 
- корень положительное число.
при 0 < ω < ∞, φ(ω) меняется от 0 до -180º.
Временные характеристики.
при T2 > T1 
Частотные характеристики: АФЧХ T2 > T1
ЛАЧХ – 
- уравнение такое же как у инерционно-форсирующего звена.
T2 > T1
2. Апериодическое неустойчивое неминимально-фазовое звено.
Уравнение:
- начало в третьем квадранте.
АФЧХ.
ЛАЧХ - 
- как у апериодического устойчивого.
3. Неустойчивое неминимально-фазовое звено второго порядка.
Уравнение:
Частотные характеристики 
- расходящиеся колебания.
ЛАЧХ – уравнение как у колебательного звена.
ξ < 0,3 – использовать номограммы поправок.
К неминимально-фазовым относятся звенья:
- неустойчивое
- неустойчивое
- устойчивое
и другие.
Особое звено (также неминимально-фазовое)
Звено запаздывания (чистого запаздывания)
Уравнение: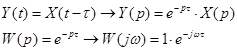 
- не зависит от ω.
φ(ω) при изменении частоты меняется от 0 до -∞. 
Временные характеристики. Звено повторяет входной сигнал без искажения, но со сдвигом во времени:
Частотные характеристики: 
АФЧХ – окружность первого радиуса.
ЛАЧХ - 
- совпадает с осью частот, а φ(ω) – от 0 до -∞.
Примеры звеньев: устройства считывания и записи информации, длинные линии электропередачи, гидротрубопроводы, транспортные линии.
Звено второго порядка
В общем случае звено второго порядка описывается дифференциальным уравнением следующего вида:
- коэффициент затухания (демпфирования)
Операторное уравнение:
Передаточная функция:
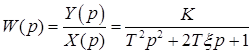
Характеристическое уравнение:
Корни характеристического уравнения:
Для корней характеристического уравнения возможны следующие случаи:
1. 
- корни вещественные положительные. В данном случае переходной процесс для данного звена – апериодический неустойчивый.
2. 
- корни комплексные с положительной вещественной частью. Переходной процесс – колебательный неустойчивый (расходящиеся колебания).
3. 
- корни чисто мнимые 
. Переходной процесс – колебания с постоянной амплитудой и частотой. Звено в этом случае называется консервативным.
4. 
- корни комплексные с отрицательной вещественной частью. Переходной процесс – колебательный устойчивый (затухающие колебания). Звено в этом случае называют колебательным.
5. 
- корни вещественные отрицательные. В данном случае переходной процесс для данного звена – апериодический устойчивый. Звено в этом случае называют апериодическим 2-го порядка.
https://lektsia.com/1x5662.html