Задача 1. В результате 5%-го бесповторного выборочного обследования были получены следующие данные о распределении рабочих механического завода по заработной плате:
| Число рабочих | Заработная плата (руб.) |
| Итого: |
Определите:1) среднюю заработную плату рабочих (с вероятностью _________);
2) долю рабочих завода с заработком выше _________ руб. (с вероятностью __________);
3) необходимую численность выборки при определении средней заработной платы, чтобы с вероятностью ______ предельная ошибка выборки не превышала _______ руб.;
4) необходимую численность выборки при определении доли рабочих с заработком свыше ________ руб., чтобы с вероятностью ________ предельная ошибка выборки не превышала _______%.
Решение. 1) Рассчитаем среднюю заработную плату рабочих в выборочной совокупности. Все расчёты сведём в таблицу.
| Заработная плата (руб.) | Число рабочих (f) | Среднее значение интервала (х) |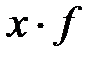 
| 
| 
| 
|
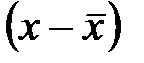
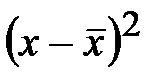
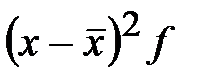
| Итого: |
Средняя выборочная в данном случае рассчитывается по формуле средней арифметической взвешенной:
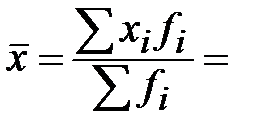
Рассчитаем дисперсию выборочной совокупности:
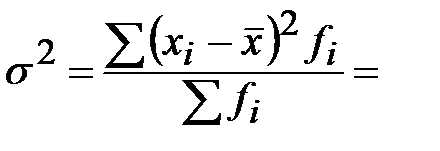
При бесповторном случайном отборе средняя ошибка выборки составит:
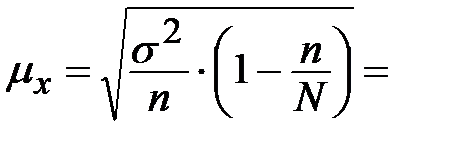
Здесь n = ________- объём выборки, а объём N генеральной совокупности вычисляется из расчёта, что выборка по условию составляет _____% от генеральной совокупности. Следовательно, N = _____________
Теперь мы можем с заданной вероятностью P = _______ рассчитать предельную ошибку выборочной средней, как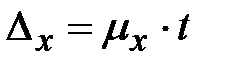 
. Значение t (коэффициента доверия) берём из таблицы 1 в приложении.
Находим: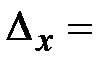 
_________
Используя полученное значение предельной ошибки пределы, в которых находится средняя заработная плата рабочих завода (генеральная средняя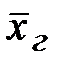 
), определим по формуле 
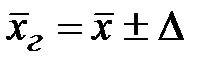. Тогда: 
____________________, следовательно, генеральная средняя находится в пределах:
______________ 
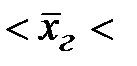_____________ или, окончательно, _________ 
________
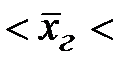2) Найдём долю рабочих завода с заработком выше _______ руб. (с вероятностью ______).
Генеральная доля равна: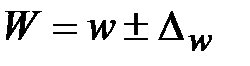 
. Чтобы определить границы генеральной доли, необходимо определить выборочную долю и ошибку выборочной доли.
Рассчитаем долю рабочих завода с заработком выше _________ руб. в выборочной совокупности:
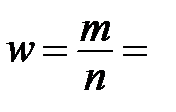
где n = _________ – общая численность выборки; m = _________ – число единиц, обладающих изучаемым признаком (число рабочих завода с заработком выше __________ руб.).
При бесповторном случайном отборе предельная ошибка выборочной доли с вероятностью __________ составит:
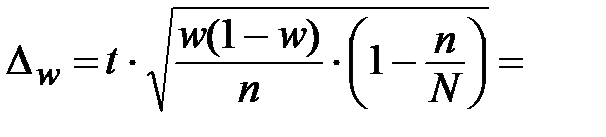
где значение t (коэффициента доверия) взято из таблицы 1.
Определим нижнюю границу генеральной доли: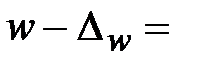 
_____________________
Определим верхнюю границу генеральной доли: 
_____________________
Тогда, с вероятностью _______ можно утверждать, что доля рабочих завода с заработком выше ________ руб. находится в пределах
______ 
______
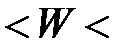3) Определим необходимую численность выборки при определении средней заработной платы, чтобы с вероятностью ________ предельная ошибка выборки не превышала ______ руб.
При бесповторном случайном отборе необходимая численность выборки вычисляется по формуле
.
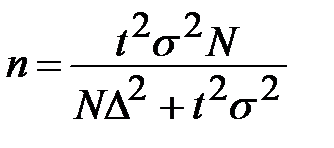Из таблицы 1 приложения по заданной вероятности Р = _______ находим значение коэффициента доверия t = _______. Остальные составляющие формулы были вычислены нами ранее: N = ________,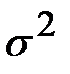 
= ___________, 
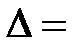________ руб. (по условию).
Тогда 
4) Определим необходимую численность выборки при определении доли рабочих с заработком свыше ________ руб., чтобы с вероятностью ________ предельная ошибка выборки не превышала ______%.
При случайном бесповторном отборе для расчета необходимой численности выборки для определения доли с заданной точностью применяется формула:
.
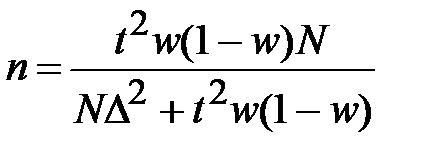Здесь N = ________, w = ___________, 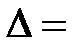_____% (по условию) или 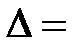_________. Из таблицы 1 приложения по заданной вероятности Р = ________ находим значение коэффициента доверия t = _____.
Тогда:
Задача 2. В порядке повторной случайной выборки было проверено ___________ бутылок, поступавших на молочный завод из предприятия общественного питания. В итоге проверки было установлено наличие _________ бракованных бутылок.
С вероятностью _________ определите: 1) ошибку репрезентативности при установлении доли бракованной посуды, поступающей на завод из предприятий общественного питания; 2) пределы, в которых находится процент бракованной посуды.
Решение. 1) Ошибка выборочной доли при случайном повторном отборе рассчитывается по формуле:
.
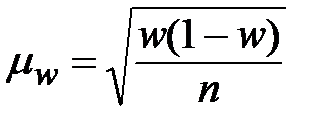Рассчитаем долю бракованных бутылок в выборочной совокупности:
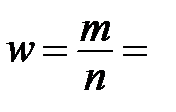
где n = _________ – общая численность выборки; m = _________ – число единиц, обладающих изучаемым признаком (количество бракованных бутылок).
Тогда ошибка доли:
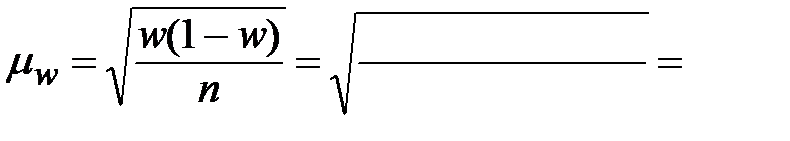
Из таблицы 1 приложения по заданной вероятности Р = ________ находим значение коэффициента доверия t = _____.
Ошибка репрезентативности с вероятностью Р = _______ равна:
________________________
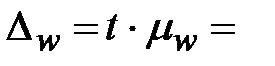2) Определим нижнюю границу генеральной доли: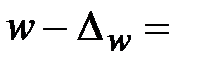 
____________________
Определим верхнюю границу генеральной доли: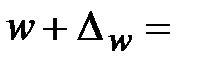 
_____________________
С вероятностью _________ можно утверждать, что пределы, в которых находится доля бракованной посуды
______ 
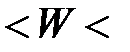______ или в процентах: ______ ______
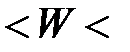Задача 3. По материалам выборочного обследования ______ предприятий оплата человеко-часа составляет в среднем _____ рубля. Определить с вероятностью _______ ошибку этой средней, если среднее квадратичное отклонение равно ______ рублям, а отбор собственно-случайный повторный. В каких пределах может колебаться средняя оплата?
Решение. Выпишем данные этой задачи:
n = _________ – объём выборки;
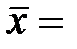________руб. – выборочная средняя (средняя оплата человеко-часа);
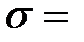________руб. – среднее квадратическое отклонение;
для вероятности P = _______ коэффициент надёжности t = ______;
отбор - ____________________________
Для заданного вида отбора ошибка средней равна:
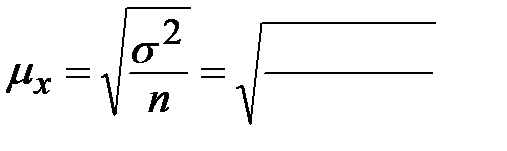
Тогда с вероятностью ___________ предельная ошибка выборочной средней будет равна:
___________________
Находим границы доверительного интервала, в которых может находится значение генеральной средней:
определяем нижнюю границу генеральной средней: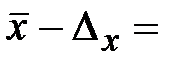 
____________________
определяем верхнюю границу генеральной средней: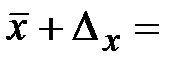 
_____________________
С вероятностью _________ можно утверждать, что пределы, в которых колеблется средняя оплата человека-часа:
_________ ________
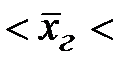Задача 4. Сколько деталей надо отобрать из _________ штук для определения ее веса, чтобы с вероятностью _______ можно было утверждать, что ошибка выборки не превышает ______ г. по выборочным испытаниям, дисперсия веса детали установлена – ______ г.
Указание: произведена случайная бесповторная выборка.
Решение. Суть данной задачи – по заданной вероятности рассчитать необходимую численность случайно-бесповторной выборки, позволяющую с определённой точностью найти выборочную среднюю. Для решения задачи требуется формула (таблица приложения):
.
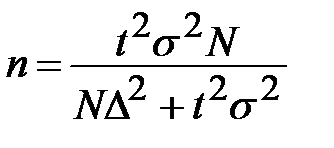Выпишем исходные данные, необходимые для решения данной задачи:
N = _________шт. – объём генеральной совокупности;
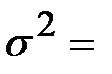________г. – дисперсия веса детали;
для вероятности P = _______ коэффициент надёжности t = ______;
______ г. – ошибка выборки.
Тогда: 
Задача 5. Из ___________ вкладчиков сберегательного банка города подвергнуто пропорциональному типическому отбору по общественным группам _________ вкладчиков, которые по размеру вкладов распределялись следующим образом:
| Общественные группы | Группы вкладчиков по размеру вкладов (тыс. руб.) | Всего вкладчиков | ||
| Рабочие | ||||
| Служащие | ||||
| Прочие | ||||
| Всего: |
Принимая во внимание, что в каждой группе произведена случайная бесповторная выборка, определите:
1) возможные пределы среднего вклада для всех вкладчиков (с вероятностью ______);
2) возможные пределы доли вкладчиков с размером вклада до _______ тыс. рублей (с вероятностью _________);
3) необходимую численность выборки при определении среднего вклада, чтобы с вероятностью _________ предельная ошибка выборки не превышала _____ рублей;
4) необходимую численность выборки при определении доли вкладчиков с размером вклада до _________ тыс. руб., чтобы с вероятностью _______ предельная ошибка выборки не превышала _____%.
Решение. Для решения данной задачи нам потребуются предварительно вычислить среднюю из внутригрупповых выборочных дисперсий и среднюю из внутригрупповых дисперсий доли.
Средняя из внутригрупповых дисперсий вычисляется по формуле:
.
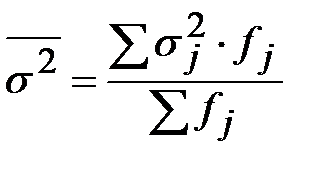Составим вспомогательные таблицы для вычисления внутригрупповых дисперсий.
| Вклады тыс. руб. |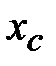 
| Рабочие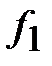
| Служащие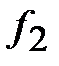
| Прочие
| 
| 
| 
|
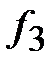
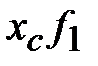
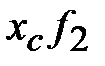
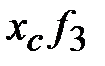
| Всего |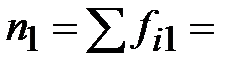 
| 
| 
| ||||
| 
|
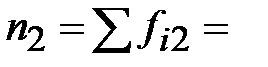
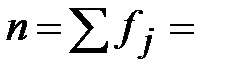
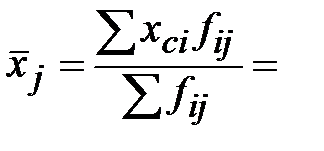
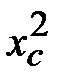
| Рабочие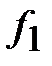
| Служащие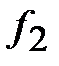
| Прочие
| 
| 
| 
|
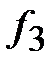
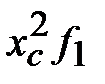
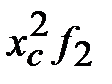
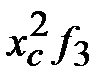
| Всего | ||||||
|
| 
|
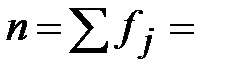
Тогда
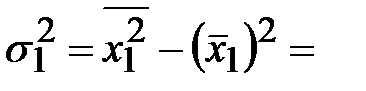
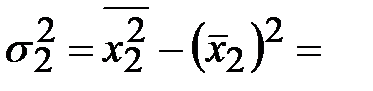
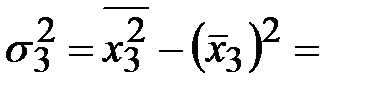
и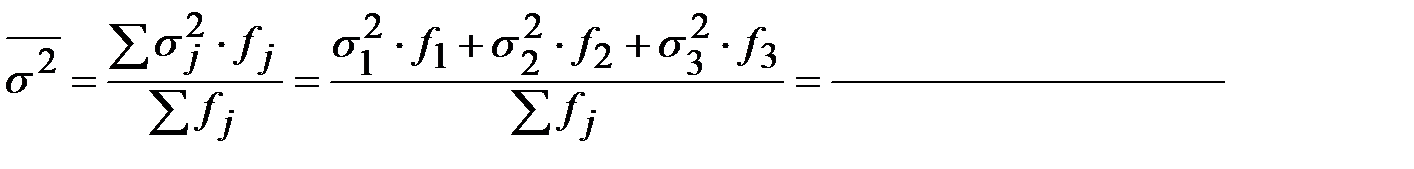 
1) Для заданной вероятности Р = ________ находим возможные пределы среднего вклада для всех вкладчиков. Предельная ошибка выборки для средней при типической выборке и бесповторном отборе определяется, как
.
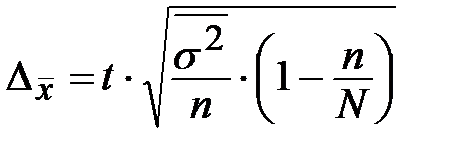Для вероятности P = _______ коэффициент надёжности t = _____; по условию N = _______.
Тогда:
определяем нижнюю границу генеральной средней: ____________________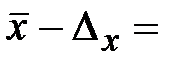
определяем верхнюю границу генеральной средней: _____________________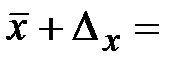
Тогда, с вероятностью ________ можно утверждать, что возможные пределы среднего вклада для всех вкладчиков:
_________ ________
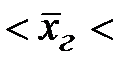2) Найдём возможные пределы доли вкладчиков с размером вклада до ________ тыс. рублей, соответствующие заданной вероятности ________.
Выборочная доля вкладчиков с размером вклада до _______ рублей (рабочие, служащие, прочие) составляет
для рабочих: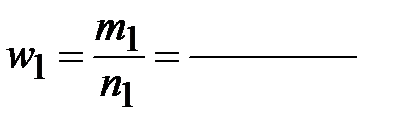 
для служащих: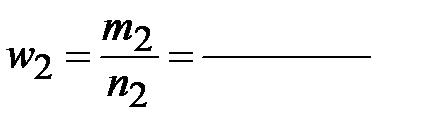 
для прочих: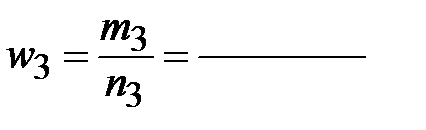 
где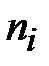 
= _________ – численность i -й группы (рабочие, служащие, прочие);
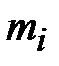= _________ – число единиц, обладающих изучаемым признаком (доля вкладчиков с размером вклада до ________ рублей).
Отсюда дисперсии долей равны:
___________
___________
___________
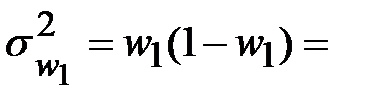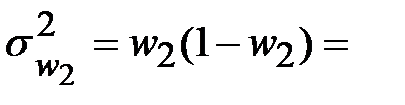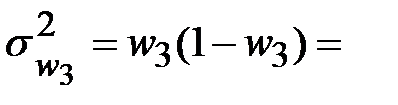Находим среднюю для дисперсий долей:
Для вероятности P = _______ коэффициент надёжности t = _____; тогда предельная ошибка выборки равна:
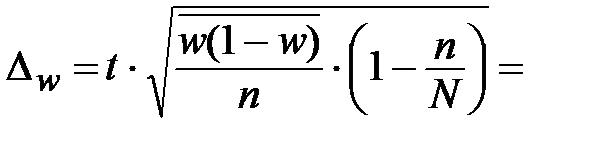
Определим нижнюю границу генеральной доли: ____________________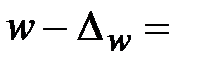
Определим верхнюю границу генеральной доли: _____________________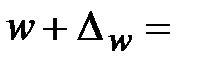
Тогда, с вероятностью ________ можно утверждать, что пределы, в которых находится доля вкладчиков с размером вклада до ________ рублей:
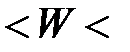______ ______ или в процентах: ______ ______
3) Найдём необходимую численность выборки при определении среднего вклада, чтобы с вероятностью ________ предельная ошибка выборки не превышала ______ рублей.
Для типической бесповторной выборки
.
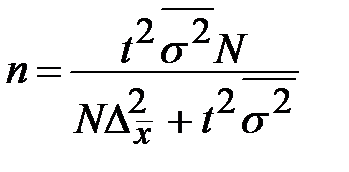Выпишем данные, требуемые для нахождения объёма выборки:
для вероятности P = _______ коэффициент надёжности t = ______;
__________; N = __________; 
________руб.
Тогда 
4) Найдём необходимую численность выборки при определении доли вкладчиков с размером вклада до _________ руб., чтобы с вероятностью _________ предельная ошибка выборки не превышала _____ %.
Для типической бесповторной выборки
.
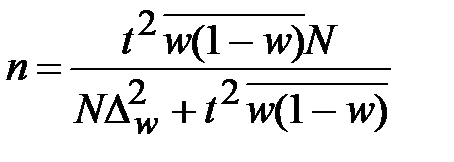Выпишем данные, требуемые для нахождения объёма выборки:
для вероятности P = _______ коэффициент надёжности t = ______;
__________; N = __________;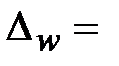 
________.
Тогда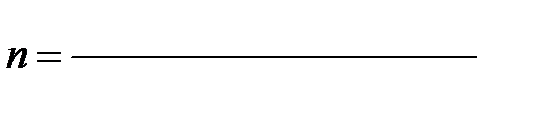
Задача 7. Из ______ коробок по _______ лимонов в каждой, поступивших в течение квартала на склад магазина, в порядке случайной бесповторной серийной выборки отобрано 7 ящиков, все фрукты в которых проверены на вес. Были получены следующие результаты:
| Коробки | |||||||
| Средний вес лимона (г) |
По этим данным установите:
1) возможные пределы среднего веса лимона в ящиках, поступивших на склад магазина (с вероятностью _________);
2) объем случайной бесповторной серийной выборки, чтобы с вероятностью ______ предельная ошибка выборки при определении среднего веса лимона не превышала ____ г.
Решение. Рассчитаем, предварительно, среднюю величину (как среднюю арифметическую простую) и межгрупповую дисперсию:
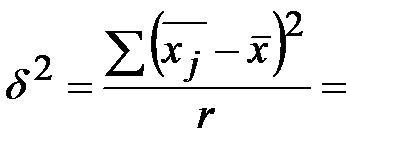
Выпишем нужные данные для решения нашей задачи: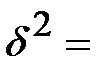 
__________ – межгрупповая дисперсия;
R = _________ – количество серий (групп) генеральной совокупности;
r = _________ – количество серий (групп) выборочной совокупности;
1) Предельная ошибка среднего значения признака при серийном бесповторном отборе определяется по формуле:
.
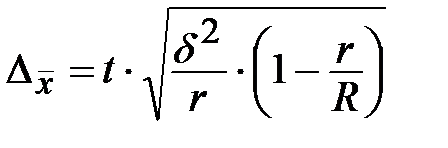Для вероятности P = _______ коэффициент надёжности t = ______. Тогда
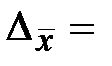
Определяем нижнюю границу генеральной средней: ____________________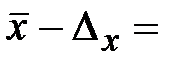
Определяем верхнюю границу генеральной средней: _____________________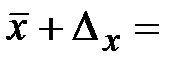
Следовательно, с вероятностью ________ можно утверждать, что возможные пределы среднего веса лимона в ящиках, поступивших на склад магазина:
_________ ________
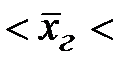2) Найдём объем случайной бесповторной серийной выборки, чтобы с вероятностью ________ предельная ошибка выборки при определении среднего веса лимона не превышала ____ г.
Для бесповторной серийной выборки
,
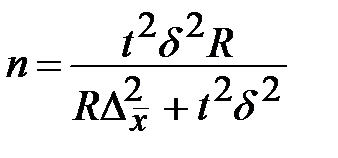где 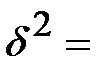__________ – межгрупповая дисперсия;
R = _________ – количество серий (групп) генеральной совокупности;
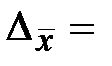_________ – предельная ошибка среднего значения;
для вероятности P = _______ коэффициент надёжности t = ______.
Тогда
Приложение
Функция Лапласа: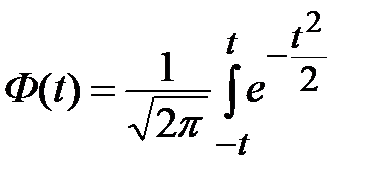 
Таблица 1. Значения функции Лапласа
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Продолжение таблицы 1.
|
|
|
|
|
Таблица 2. Средняя ошибка выборочных средней и доли для разных видов выборки
| Вид выборки | Отбор | |
| Повторный | Бесповторный | |
| Количественный признак | ||
| Собственно-случайная |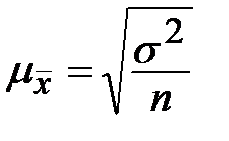 
| 
|
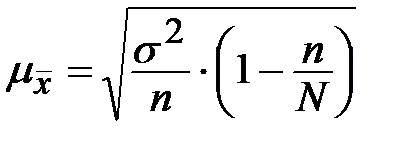
Механическая 
| - | - |
| Типическая (стратифицированная) |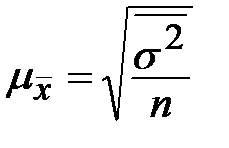 
| 
|
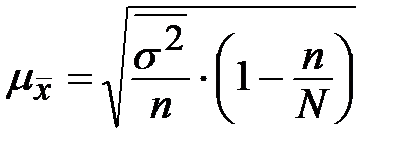
| Серийная |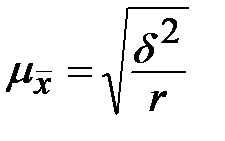 
| 
|
| Альтернативный признак | ||
| Собственно-случайная |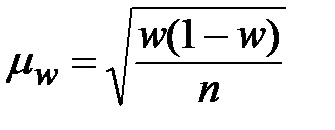 
| 
|
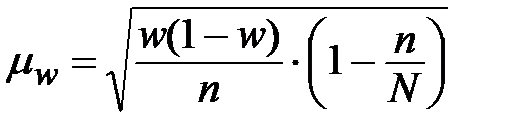
Механическая 
| - | - |
| Типическая (стратифицированная) |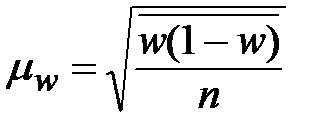 
| 
|
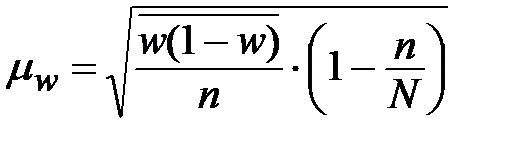
| Серийная |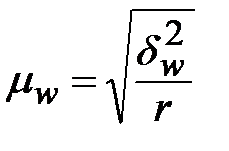 
| 
|
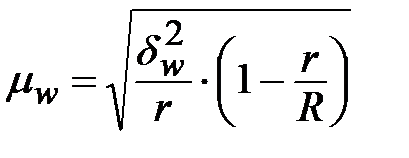
Где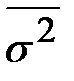 
– средняя из внутригрупповых выборочных дисперсий;
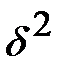– межгрупповая дисперсия;
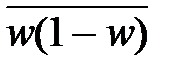– средняя из внутригрупповых дисперсий доли;
r – число отобранных серий (групп), R – общее число серий (групп);
Таблица 3. Предельная ошибка выборки для средней и доли для разных видов выборочного наблюдения
| Вид выборки | Отбор | |
| Повторный | Бесповторный | |
| Количественный признак | ||
| Собственно-случайная |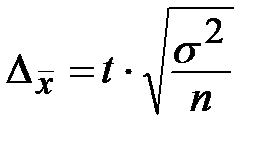 
| 
|
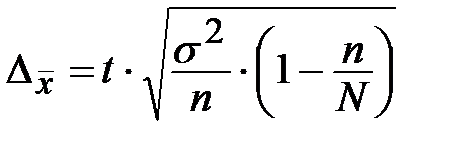
| Механическая
| - | - |
| Типическая (стратифицированная) |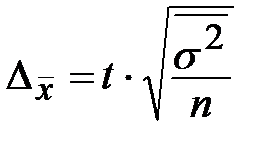 
|
|
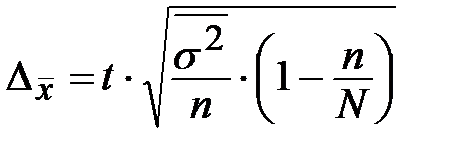
| Серийная |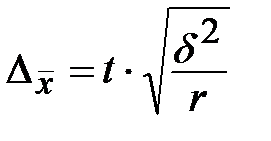 
|
|
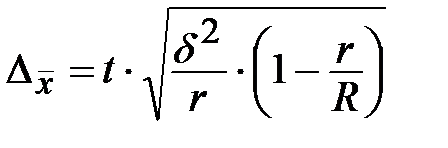
| Альтернативный признак | ||
| Собственно-случайная |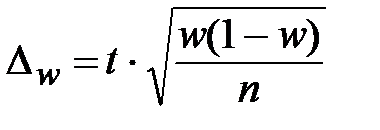 
| 
|
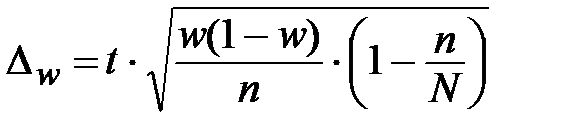
Механическая 
| - | - |
| Типическая (стратифицированная) | 
| 
|
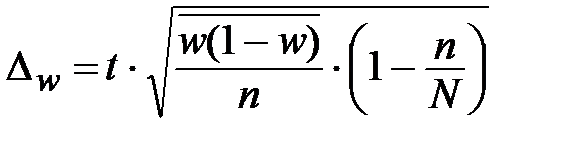
| Серийная |