При обходе в ширину, узлы графа, равноудаленные от начальной вершины обрабатываются одним шагом алгоритма. За счет этого, алгоритм находит путь, который содержит наименьшее количество узлов[5].
На рис. 47 показан порядок обработки вершин при поиске пути из узла B. Черным цветом выделены вершины, не достижимые из стартовой. Пунктирная линия изображает возможную альтернативу (вершина F может быть добавлена с использованием дуги (D, F) или дуги (E, F)).
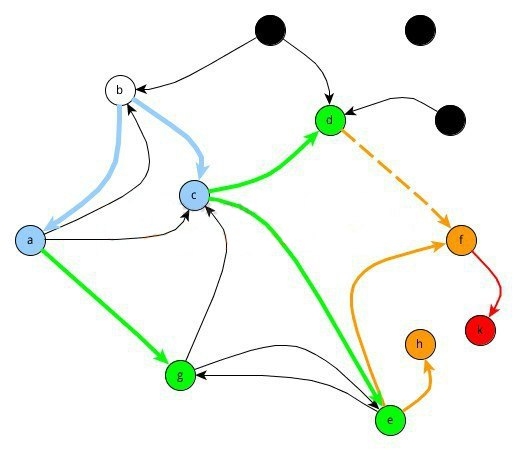
Рис.47. Обход графа в ширину
Для работы такого алгоритма необходимо поддерживать очередь необработанных вершин (именно очередь, т.к. выбор вместо нее стека превратит наш алгоритм в поиск в глубину). Кроме того, чуть-чуть усложняется восстановление найденного пути — нам известно множество вершин, обрабатываемых на каждом шаге, поэтому чтобы точно восстановить путь, нам придется хранить список использованных дуг.
Листинг 2 алгоритм поиска в ширину:
1. начало; функция breadth(G, Queue_add, Queue_proc, Finish, Res)
; обход графа в ширину
; G - граф,
; Queue_add - очередь добавленных вершин (не обработанных)
; Queue_proc - очередь обработанных вершин
; Finish - конечная вершина
; Res - список использованных дуг
2. если Queue пуст - вернуть (false, Res);
3. получить H узел из начала Queue_add;
4. если H = Finish - вернуть (true, Res);
5. adj_nodes:= список вершин, смежных с H;
6. удалить из adj_nodes вершины, присутствующие в Queue_add или Queue_proc;
7. удалить H из Queue_add, добавить H в Queue_proc;
8. добавить в конец Queue_add вершины из adj_nodes;
9. добавить в Res дуги между узлом H и вершинами из adj_nodes;
10. вернуть breadth(G, Queue_add, Queue_proc, Finish, Res);
11. конец.
По алгоритму листинг 2, поиск продолжается пока не будут обработаны все доступные вершины (п. 2), либо не будет найдена нужная вершина (п.4). Функция breadth выбирает вершину из начала очереди обработки (п.3), и добавляет новые в конец (п.8) — за счет этого обеспечивается требуемый порядок обхода — чем более узел удален от стартовой вершины — тем позже он будет обработан. Для устранения зацикливания алгоритма, в очередь добавляются только вершины, которые не были обработаны или добавлены в очередь обработки на предыдущих шагах (п.6).
Приведенный алгоритм возвращает не путь, а список дуг, по которому можно восстановить кратчайшие пути между стартовой и всеми обработанными вершинами (листинг 3).
Листинг 3 алгоритм восстановления пути:
1. начало; функция path(Start, Finish, Edges)
; восстановление пути между двумя вершинами по дугам
; Start - начало пути
; Finish - конец пути
; Edges - дуги, полученные поиском в ширину
2. если в Edges нет дуги (Start, Finish) - переход к п.3;
2.1. вернуть список из одной дуги (Start, Finish);
3. получить дугу (X, Finish) из Edges;
4. PartPath:= path(Start, X, Edges)
5. PartPath:= (X, Finish) + PartPath;
6. конец (вернуть PartPath).
Если алгоритм поиска в ширину (функция breadth) вернул true — то соответствующий набор дуг гарантированно содержит искомый путь и функция path в п.3 найдет дугу, принадлежащую этому пути.
Алгоритм Дейкстры
Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное. Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом[6].
Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется граф G=(V, E). Каждая из вершин, входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false. Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например, максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель). Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:
distance[t]=distance[s]+весинцидентного s и t ребра;
distance[u]=distance[s]+ весинцидентного s и u ребра.
Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.
Для примера возьмем такой ориентированный граф G (рис.47):
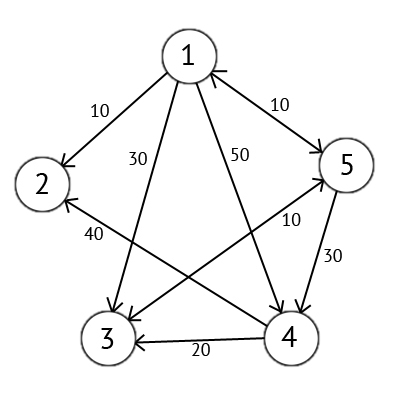
Рис.47. Ориентированный граф G
Этот граф мы можем представить в виде матрицы С (рис.48):
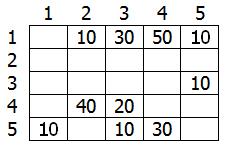
Рис.48. Матрица С
Возьмем в качестве источника вершину 1. Это значит, что мы будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5.Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере (рис.50).
Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.

Рис.50. Присвоение вершинам графа меток
Далее выберем такую вершину W, которая имеет минимальную метку (сейчас это вершина 1) и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.
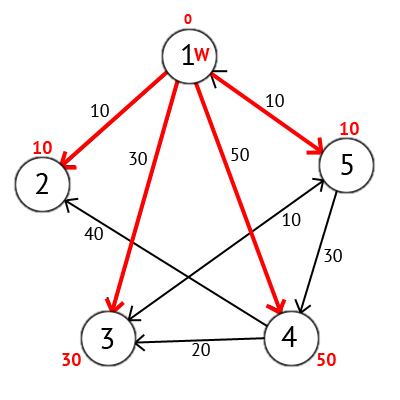
Рис.51. Произошедшие изменения в графе
После того как мы рассмотрели все вершины, в которые есть прямой путь из W, вершину W мы отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них мы выберем как W.
Мы выберем вершину 2. Но из нее нет ни одного исходящего пути, поэтому мы сразу отмечаем эту вершину как посещенную и переходим к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму
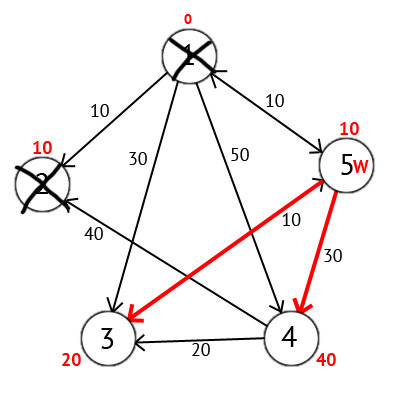
Рис.52. Новый измененный граф
Исходя из картинки мы можем увидеть, что метки 3-ей и 4-ой вершин стали меньше, тоесть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть непосещенные вершины. Выполнив все действия получим такой результат:
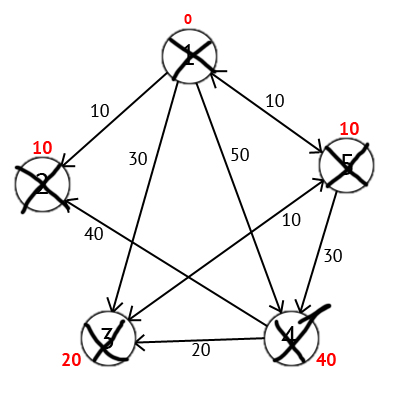
Рис.52. Граф после выполнения всех операций
Также есть вектор Р, исходя из которого можно построить кратчайшие маршруты. По количеству элементов этот вектор равен количеству вершин в графе, Каждый элемент содержит последнюю промежуточную вершину на кратчайшем пути между вершиной-источником и конечной вершиной. В начале алгоритма все элементы вектора Р равны вершине источнику (в нашем случае Р = {1, 1, 1, 1, 1}). Далее на этапе пересчета значения метки для рассматриваемой вершины, в случае если метка рассматриваемой вершины меняется на меньшую, в массив Р мы записываем значение текущей вершины W. Например: у 3-ей вершины была метка со значением «30», при W=1. Далее при W=5, метка 3-ей вершины изменилась на «20», следовательно мы запишем значение в вектор Р — Р[3]=5. Также при W=5 изменилось значение метки у 4-й вершины (было «50», стало «40»), значит нужно присвоить 4-му элементу вектора Р значение W — P[4]=5. В результате получим вектор Р = {1, 1, 5, 5, 1}.
Зная, что в каждом элементе вектора Р записана последняя промежуточная вершина на пути между источником и конечной вершиной, мы можем получить и сам кратчайший маршрут.
Алгоритм Флойда
Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным. Алгоритм Флойда – Уоршелла – динамическийалгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных[6].
Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D[][] графа G=(V, E), в котором каждая вершина пронумерована от 1 до |V|. Эта матрица имеет размер |V|´|V|, и каждому ее элементу D[i][j] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время). Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D[i][j] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D[i][i]) нужно обнулить. А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.
Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если D[i][k]+D[k][j]<D[i][j] то D[i][j] ←D[i][k]+D[k][j]
Кратчайший путь из вершины i в вершину j может проходить, как только через них самих, так и через множество других вершин k∈(1, …, |V|). Оптимальным из i в j будет путь или не проходящий через k, или проходящий. Заключить о наличии второго случая, значит установить, что такой путь идет из i до k, а затем из k до j, поэтому должно заменить, значение кратчайшего пути D[i][j] суммой D[i][k]+D[k][j].
Сейчас детально разберем последовательность выполняемых им действий.
Положим, что в качестве матрицы смежности, каждый элемент которой хранит вес некоторого ребра, была задана следующая матрица:
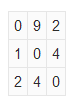
Рис.53. Заданная матрица
Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Вот собственно сам этот граф:
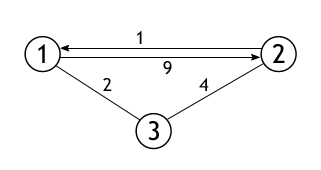
Рис.54. Заданный граф
Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.

Рис.54. Выполнение основной части алгоритма
В данной таблице показаны 27 шагов выполнения основной части алгоритма. Их столько по той причине, что время выполнения метода равно O(|V|3). Наш граф имеет 3 вершины, а 33=27. Первая замена происходит на итерации, при которой k=1, i=2, а j=3. В тот момент D[2][1]=1, D[1][3]=2, D[2][3]=4. Условие истинно, т. е. D[1][3]+D[3][2]=3, а 3<4, следовательно, элемент матрицы D[2][3] получает новое значение. Следующий шаг, когда условие также истинно привносит изменения в элемент, расположенный на пересечении второй строки и третьего столбца.