Алгоритмы нахождения максимального потока транспортной сети.

Метод Форда Фалкерсона решает задачу нахождения максимального потока в транспортной сети. Метод Форда базируется на трёх важных концепциях, которые выходят за рамки данного метода и применяются во многих потоковых алгоритмах и задачах. Это – остаточные сети, увеличивающие пути и разрезы. Данные концепции лежат в основе теоремы о максимальном потоке и минимальном разрезе, которая определяет значение максимального потока с помощью разрезов транспортной сети[7].

Метод Форда - Фалкерсона является итеративным. Вначале величине потока присваивается значение 0: f (u,v) = 0 для всех u,v ∈ V. На каждой итерации величина потока увеличивается посредством поиска «увеличивающего пути». Этот процесс повторяется до тех пор, пока уже невозможно отыскать увеличивающий путь. В теореме о максималь­ном потоке и минимальном разрезе будет показано, что по завершении данного процесса получается максимальный поток.

Ford_Fulkerson_Method(G,s, t)

1 Задаем начальное значение потока f равным 0

2 while (Пока) существует увеличивающий путь р

3 do увеличиваем поток f вдоль пути р

4 return f

 

 

Остаточные сети

 

Интуитивно понятно, что если заданы некоторая транспортная сеть и поток, то остаточная сеть — это сеть, состоящая из ребер, допускающих увеличение потока. Более строго, пусть задана транспортная сеть G = (V, Е) с источником s и стоком t. Пусть f — некоторый поток в G. Рассмотрим пару вершин u,v ∈ V. Величина дополнительного потока, который мы можем направить из и в v, не превысив пропускную способность с (u, v), является остаточной пропускной способностью (residual capacity) ребра (u, v), и задается формулой

(u, v) = c (u, v) - f (u, v) [7].

Например, если c(u,v) = 16 и f(u,v) = 11, то f(u,v) можно увеличить на (u,v) = 5, не нарушив ограничение пропускной способности для ребра (u, v). Когда поток f(u,v) отрицателен, остаточная пропускная способность (u,v) больше, чем пропускная способность с (u, v). Так, если с (u, v) = 16 и f (u, v) = = —4, то остаточная пропускная способность (и, v) = 20. Эту ситуацию можно интерпретировать следующим образом: существует поток величиной 4 единицы из v в u,который можно аннулировать, направив 4 единицы потока из u в v. Затем можно направить еще 16 единиц из u в v, не нарушив ограничение пропускной способности для ребра (u, v). Таким образом, начиная с потока f (u, v) = —4, мы направили дополнительные 20 единиц потока, прежде чем достигли ограничения пропускной способности.

Для заданной транспортной сети G = (V, E) и потока f, остаточной сетью в G, порожденной потоком f, является сеть = (V,

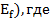
= {(u,v) ∈ V ˟ V: 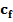(u, v) > 0}

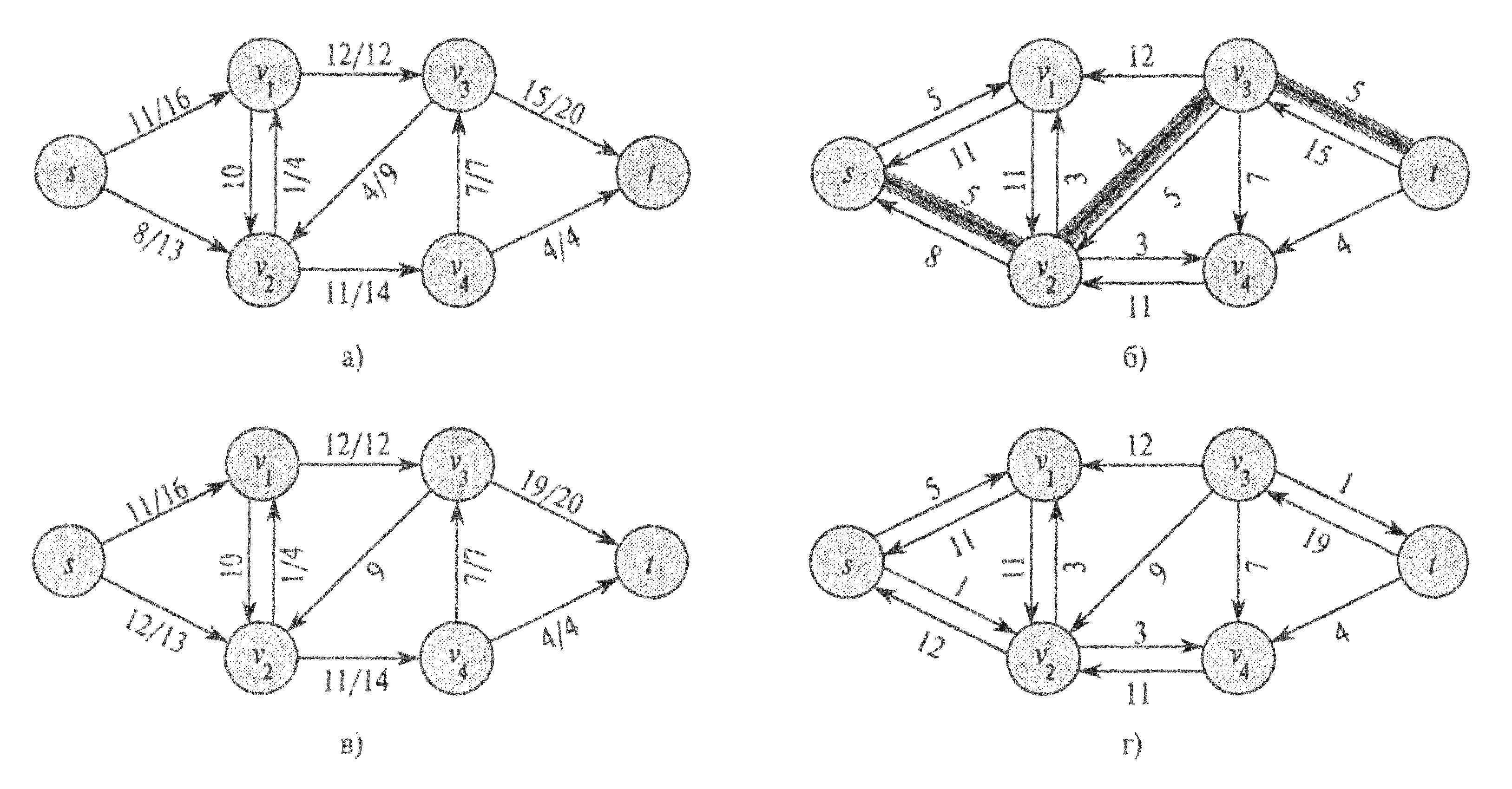
Рис. 57. а) Транспортная сеть G и поток f. б) Остаточ­ная сеть с выделенным увеличивающим путем; его остаточная пропускная способ­ность равна 4. в) Поток в сети G, полученный в результате увеличения потока вдоль пути р на величину его остаточной пропускной способности 4. г) Остаточная сеть, порожденная потоком, показанным в части в)

Ребрами являются или ребра Е, или обратные им. Если f(u, v) < с (u, v) для некоторого ребра (u, v) ∈ Е, то (u, v) = с (u, v) — f (u, v) > 0 и (u, v ) ∈ . Если f ( и, v) > 0 для некоторого ребра (u, v) ∈ Е, то f (v, u) < 0. В таком случае 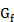(v,u) = c(v,u) — f (v, и) > 0 и, следовательно, (v,u) ∈ . Если в исходной сети нет ни ребра (u, v), ни (u, u), то c(u,v) = с (v, u) = 0, f(u, v) = f (v, u) = = 0, и (u, v) = (v, и) = 0. Таким образом, можно сделать вывод, что ребро (u, v) может оказаться в остаточной сети только в том случае, если хотя бы одно из ребер (u, v) или (v, u) присутствует в исходной транспортной сети, поэтому .

Обратите внимание, что остаточная сеть 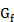является транспортной сетью со зна­чениями пропускных способностей, заданными с/. Следующая лемма показывает, как поток в остаточной сети связан с потоком в исходной транспортной сети.

Лемма 24. Пусть G = (V, Е) — транспортная сеть с источником sи стоком t, а f — поток в G. Пусть 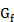— остаточная сеть в G, порожденная потоком f, а f’ — поток в 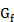. Тогда сумма потоков f+f' является потоком в G, и величина этого потока равна |f + f'| = |f| + |f'|.

13.2 Увеличивающие пути

Для заданных транспортной сети G = (V, Е) и потока f увеличивающим путем (augmenting path) р является простой путь из s в tв остаточной сети 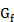[7].

Согласно определению остаточной сети, каждое ребро (u, v) увеличивающего пути допускает некоторый дополнительный положительный поток из и в v без нарушения ограничения пропускной способности для данного ребра.

Выделенный путь является увеличивающим путем. Рассматри­вая представленную на рисунке остаточную сеть как некоторую транспортную сеть, можно увеличивать поток вдоль каждого ребра данного пути вплоть до 4 еди­ниц, не нарушая ограничений пропускной способности, поскольку наименьшая остаточная пропускная способность на данном пути составляет () = 4. Максимальная величина, на которую можно увеличить поток вдоль каждого реб­ра увеличивающего пути р, называется остаточной пропускной способностью (residual capacity) р и задается формулой

(p) = min{ }

 

Лемма 25. Пусть G = (V, Е) — транспортная сеть, а f — некоторый поток в G, и пусть р — некоторый увеличивающий путь в 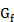. Определим функцию 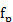:V х V —> R следующим образом:

 

Вытекающее из данной леммы следствие показывает, что если добавить к f, то мы получим новый поток в G, величина которого ближе к максимальной.

13.3 Разрезы транспортных сетей

В методе Форда-Фалкерсона производится неоднократное увеличение пото­ка вдоль увеличивающих путей до тех пор, пока не будет найден максимальный поток. В теореме о максимальном потоке и минимальном разрезе, которую мы вскоре докажем, утверждается, что поток является максимальным тогда и только тогда, когда его остаточная сеть не содержит увеличивающих путей. Однако для доказательства данной теоремы нам понадобится ввести понятие разреза транс­портной сети[7].

Разрезом (cut) (S, Т) транспортной сети G = (V, Е) называется разбиение множества вершин на множества S и Т = V- S, такие что s∈ S, a t ∈ Т. Если f — поток, то чистый поток (net flow) через разрез (S, Т) по определению равен f (S, Т). Пропускной способностью (capacity) разреза (S, Т) является с (S, Т). Минимальным разрезом (minimum cut) сети является разрез, пропускная способность которого среди всех разрезов сети минимальна.

На рис. 58 показан разрез ({s }, { ,t}) транспортной сети. Чистый поток через данный разрез равен:

f ( + f ( + f (

Чистый поток через разрез может включать в себя отрицательные потоки между вершинами, но пропускная способность разреза слагается исключительно из неотрицательных значений. Иными словами, чистый поток через разрез (S, Т) составляется из положительных потоков в обоих направ­лениях; положительный поток из S в Тприбавляется, а положительный поток из Т в S вычитается. С другой стороны, пропускная способность разреза (S, T) вычисляется только по ребрам, идущим из S в Т. Ребра, ведущие из Т в S, не участвуют в вычислении с (S, Т).

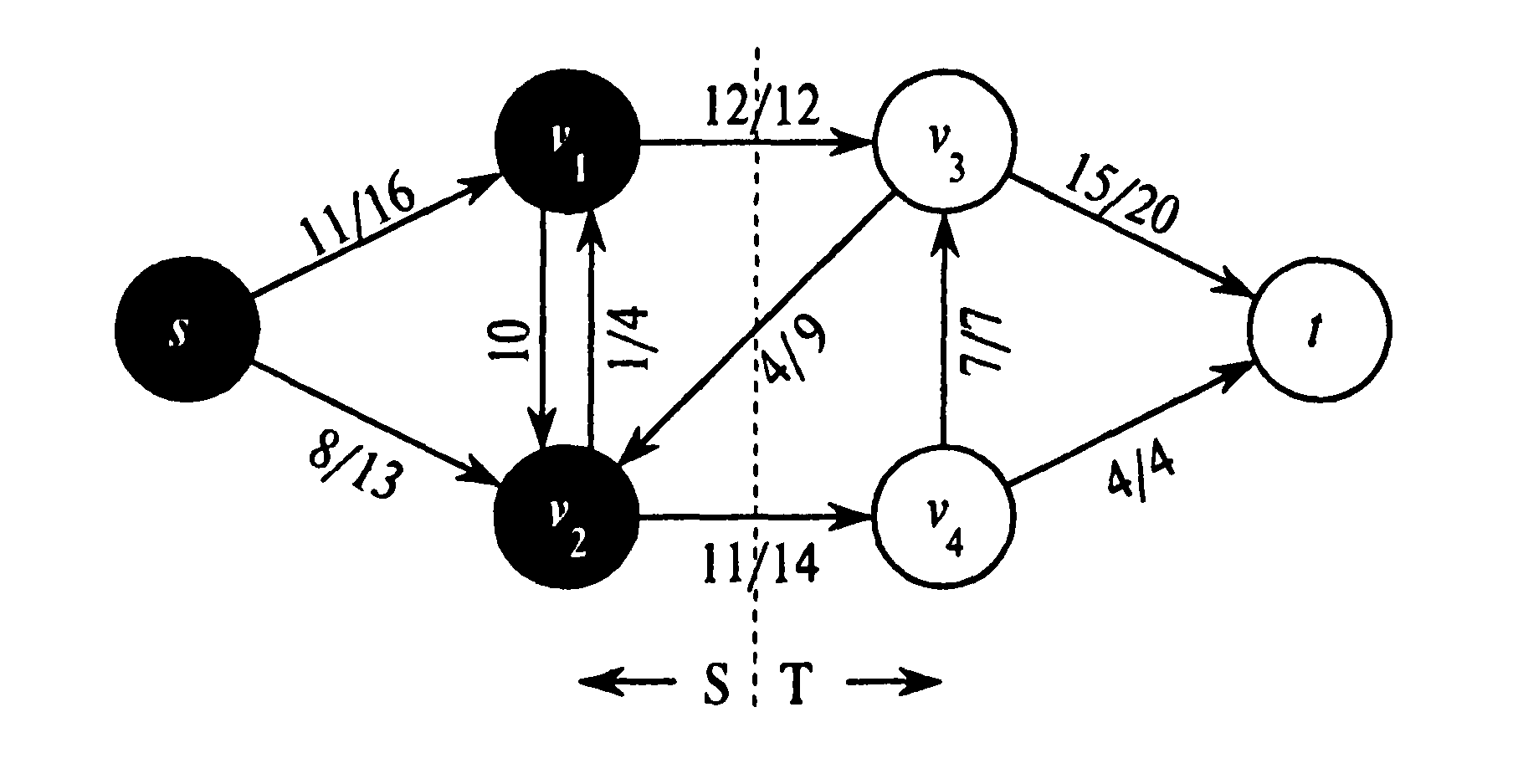
Рисунок 58. Разрез (S, Т) транспортной се­ти

 

Лемма 26. Пусть f — некоторый поток в транспортной сети G с источником s и стоком t, и пусть (S, Т) — разрез G. Тогда чистый поток через (S, Т) равен f(S,T) = |f|

Следствие. Величина любого потока / в транспортной сети G не превышает пропускную способность произвольного разреза G.

 

Теорема. (О максимальном потоке и минимальном разрезе). Если / — не­который поток в транспортной сети G = (V, Е) с источником s и стоком t, то следующие утверждения эквивалентны.

 

1. f — максимальный поток в G.

2. Остаточная сеть 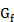не содержит увеличивающих путей.

3. |f| = с (S, Т) для некоторого разреза (S, Т) сети G.

 

 

Список использованной литературы

 

1. Н.Вирт. Алгоритмы и структуры данных.-М.:"Мир",1989.

2. Окулов С. М. Абстрактные типы данных. — М.: БИНОМ. Лаборатория знаний, 2002. — 341 с.

3. Роберт Седжвик. Фундаментальные алгоритмы на C. Части 1 - 5. Анализ. Структуры данных. Сортировка. Поиск. Алгоритмы на графах. 2003. — 1136 с.

4. Кормен, Томас X., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клиффорд. Алгоритмы: построение и анализ, 2-е издание. — М.:Издат. дом "Вильямс", 2005. —1296с.

5. Седжвик Роберт. Фундаментальные алгоритмы на C++. Часть 5: Алгоритмы на графах. — СПб.: ООО «ДиаСофтЮП», 2002. —

496 с.

6. Кристофидес Н. Теория графов. Алгоритмический подход. — М.: Мир, 1978. — 432 с.

7. Ахо, Альфред, В., Хопкрофт, Джон, Ульман, Джеффри, Д. Структуры данных и алгоритмы. — М.: Издательский дом "Вильямс", 2000. — 384 с.

 

 

Содержание

1. Понятие сложности алгоритма…………………………………....3

1.1 Пространственная и временная сложность…………………...9

1.2 Классы сложности……………………………………………..12

1.3 О-сложность алгоритмов……………………………………...14

2. Элементарные структуры данных……………………………….22

2.1 Массивы…………………………………………………..……23

2.2 Список………………………………………………………….24

3. Абстрактные типы данных……………………………………….26

3.1 Очередь…………………………………………………………28

3.2 Стек……………………………………………………………..29

4. Рекурсия и деревья………………………………………………..30

4.1 Рекурсивные алгоритмы………………………………………32

4.2 Деревья…………………………………………………………42

4.3 Обход дерева…………………………………………………...53

5. Элементарные методы сортировки………………………………60

5.1 Правила игры…………………………………………………..63

5.2 Сортировка выбором…………………………………………..71

5.3 Сортировка вставками………………………………………...74

5.4 Пузырьковая сортировка……………………………………...79

5.5 Характеристики производительности элементарных методов сортировки……...……………………………………………………82

5.6 Сортировка методом Шелла…………………………………..91

5.7 Быстрая сортировка……………………………………………95

5.8 Характеристики производительности быстрой сортировки103

5.9 Сортировка слиянием………………………………………...107

5.10 Двухпутевое слияние……………………………………….109

6.Поиск……………………………………………………………...113

6.1 Поиск с использованием индексации по ключам………….114

6.2 Последовательный поиск……………………………………119

6.3 Бинарный поиск………………………………………………126

7. Бинарные деревья поиска……………………………………….131

7.1 Производительность деревьев поиска………………………140

8. Необходимость балансировки деревьев………………………..146

8.1 Рандомизированные BST-деревья…………………………..150

9. Красно-черные деревья………………………………………….158

9.1 Свойства красно черных деревьев…………………………..159

9.2 Повороты……………………………………………………...161

9.3 Вставка………………………………………………………..163

9.4 Удаление……………………………………………………...165

10. Точный поиск подстрок в строке………………………….…..169

10.1 Простейшие алгоритмы поиска подстрок………………....171

10.2 Алгоритм Робина-Карпа……………………………………173

11. Алгоритмы на графах…………………………………………..180

11.1 Свойства и типы графов……………………………………180

11.2 Глоссарий……………………………………………………184

11.3 АТД графа…………………………………………………...194

11.4 Алгоритмы обхода графа в глубину……………………….203

11.5 Алгоритмы обхода графа в ширину……………………….205

11.6 Алгоритм Дейкстры………………………………………...209

11.7 Алгоритм Флойда…………………………………………...215

12. Алгоритм нахождения минимального остовного дерева в графе…...……………………………………………………………219

12.1 Алгоритм Дейкстры-Примы………………………………..220

12.2 Алгоритм Крускана…………………………………………224

13. Алгоритмы нахождения максимального потока транспортной сети…………………………………………………………………..228

13.1 Остаточные сети………………………..…………………...228

13.2 Увеличивающие пути………………………………………230

13.3 Разрезы транспортной сети………………………………...231

14. Список литературы……………………………………………..234