Расчетно-графическая работа № 6
Расчет переходных процессов в линейных электрических цепях
первого порядка классическим методом
Задание
1. На откидном листе изобразить электрическую цепь, подлежащую расчету, привести численные значения параметров и задающих источников цепи.
2. Рассчитать закон изменения указанного преподавателем тока классическим методом на двух интервалах времени: t 1 < t < t 2, t > t 2, определяемых последовательным срабатыванием ключей K 1 и K 2 соответственно в моменты времени t 1 и t 2. Предполагается, что до момента t 1 срабатывания первого ключа цепь находилась в установившемся режиме. Момент t 2 выбираем из условия: t 2 = 2t1, где t1 – постоянная времени цепи, образованной в результате первой коммутации.
3. Построить график зависимости тока i (t), заданного преподавателем, на всех интервалах времени.
6.2. Выбор варианта и расчет параметров элементов цепи
1. Расчетная цепь выбирается с помощью таблицы и рис. 6.1 в соответствии с номером варианта, задаваемым преподавателем. В таблице ТС – тип срабатывания, К 1 – первый ключ, К 2 – второй ключ.
2. Параметры элементов цепи выбираются в соответствии со следующими правилами:
a) для четных номеров вариантов L = 60 мГн, С = 200 мкФ;
б) для нечетных номеров вариантов L = 20 мГн, С = 100 мкФ;
в) величины сопротивлений R для всех вариантов равны:
– для четных ветвей R = 10 + 10 AR Ом,
– для нечетных ветвей R = 20 + 5 AR Ом,
где AR – сумма цифр номера варианта.
3. Заданные параметры источников рассчитываются по формуле
Е = 10(N + M) В,
где N – номер группы; M – шифр направления бакалавриата: для АТ – 1; АСУ –1,5; ЭС – 2; АЭП (АТПП) – 2,5; ТК – 3; КТЭИ – 3,5; АТП – 4; АУЦ – 4,5; ЭВТ – 5; КОБ – 5,5; КЗИ – 6, КСК – 7.
|
|
4. Ключи срабатывают поочередно в соответствии с указанными номерами. Тип срабатывания (замыкание, размыкание) задается в таблице.
5. Ток (или напряжение), функцию изменения во времени которого требуется определить, указывается преподавателем.
Таблица
| Варианты | Граф | Расположение элементов в ветвях цепи | |||||||
| Ключ | Е | R | L | С | |||||
| К 1 | ТС | К 2 | ТС | ||||||
| 1, 26, 51, 76 | а | Зам. | Разм. | 1,3,5,7 | – | ||||
| 2, 27, 52, 77 | б | Зам. | Разм. | 1,2,3,4 | – | ||||
| 3, 28, 53, 78 | в | Разм. | Зам. | 1,3,5,7 | – | ||||
| 4, 29, 54, 79 | г | Зам. | Зам. | 1,2,4,5,7 | – | ||||
| 5, 30, 55, 80 | д | Зам. | Зам. | 1,2,4,5,6 | – | ||||
| 6, 31, 56, 81 | е | Разм. | Зам. | 3,4,5,6 | – | ||||
| 7, 32, 57, 82 | а | Разм. | Зам. | 1,2,4,5,7 | – | ||||
| 8, 33, 58, 83 | б | Зам. | Разм. | 2,3,4,5, | – | ||||
| 9, 34, 59, 84 | в | Разм. | Зам. | 3,4,5,7 | – | ||||
| 10, 35, 60, 85 | г | Зам. | Разм. | 1,3,4,6 | – | ||||
| 11, 36, 61, 86 | д | Разм. | Зам. | 3,4,5,6 | – | ||||
| 12, 37, 62, 87 | е | Зам. | Разм. | 1,3,4,5,6 | – | ||||
| 13, 38, 63, 88 | а | Разм. | Зам. | 1,3,5,7 | – | ||||
| 14, 39, 64, 89 | б | Зам. | Разм. | 1,2,3,4 | – | ||||
| 15, 40, 65, 90 | в | Разм. | Зам. | 1,3,4,5,7 | – | ||||
| 16, 41, 66, 91 | г | Разм. | Разм. | 1,2,4,5,7 | – | ||||
| 17, 42, 67, 92 | д | Разм. | Разм. | 1,2,4,6,7 | – | ||||
| 18, 43, 68, 93 | е | Зам. | Разм. | 3,4,5,6 | – | ||||
| 19, 44, 69, 94 | а | Разм. | Зам. | 1,2,4,5,6 | – | ||||
| 20, 45, 70, 95 | б | Разм. | Разм. | 1,23,4 | – | ||||
| 21, 46, 71, 96 | в | Разм. | Зам. | 3,4,5,7 | – | ||||
| 22, 47, 72, 97 | г | Зам. | Разм. | 1,2,4,5,7 | – | ||||
| 23, 48, 73, 98 | д | Разм. | Зам. | 3,4,6,7 | – | ||||
| 24, 49, 74, 99 | е | Зам. | Зам. | 1,2,4,5,6 | – | ||||
| 25, 50, 75, 100 | д | Разм. | Зам. | 1,3,4,5,7 | – |
|
|
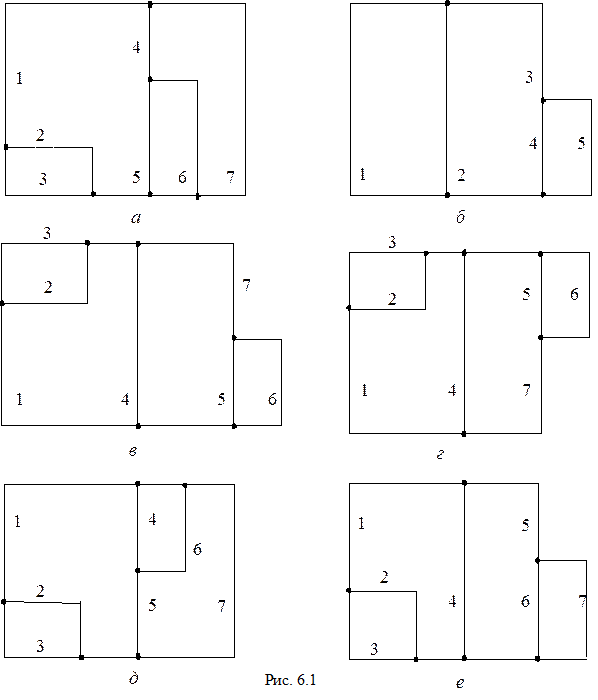
Основные теоретические сведения
Расчет переходных процессов в цепях I порядка классическим методом основан на решении дифференциального уравнения цепи.
Дифференциальное уравнение цепи может быть получено методом исключения из системы уравнений Кирхгофа для мгновенных значений, описывающей послекоммутационную цепь.
Связь между током и напряжением на реактивных элементах цепи задается дифференциальными зависимостями:
на емкости
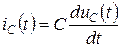 ; (6.1)
; (6.1)
на индуктивности
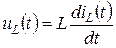 . (6.2)
. (6.2)
В полученном неоднородном дифференциальном уравнении коэффициенты левой части зависят только от параметров пассивных элементов цепи и связей между ними, а коэффициенты правой части – от задающих воздействий (параметров) источников.
Решение дифференциального уравнения цепи ищут в виде суммы принужденной (частное решение неоднородного дифференциального уравнения) и свободной составляющей (общее решение неоднородного дифференциального уравнения)
i (t) = iпр + iсв. (6.3)
Поскольку общее решение неоднородного дифференциального уравнения определяется как сумма экспонент с различными коэффициентами (постоянными интегрирования), для цепей I порядка свободная составляющая i св = Aept, где p – корень характеристического уравнения цепи.
Характеристическое уравнение цепи может быть получено путем алгебраизации (с применением преобразований Лапласа) однородного дифференциального уравнения, полученного из неоднородного дифференциального уравнения цепи путем приравнивания его правойчастик нулю[1].
|
|
Характеристическое уравнение также может быть получено путем применения метода входного сопротивления. В данном случае из цепи исключаются источники традиционным в теоретической электротехнике способом (ветви с источниками тока разрываются, источники напряжения замыкаются накоротко) и осуществляется замена j w® p. При этом сопротивление индуктивности условно приравнивается pL, а емкости 1/(pC). Далее в произвольной ветви цепь размыкается, и относительно точек разрыва записывается входное сопротивление Z (p). Выражение Z (p) = 0 является искомым характеристическим уравнением.
Корень характеристического уравнения цепи I порядка может быть найден с помощью постоянной времени цепи t, которая численно равна промежутку времени, в течение которого свободная составляющая изменяется в e раз.