Частотные характеристики

Если на входе линейной разомкнутой системы или звена подать гармоническое возмущение х(t) (рис. 23), то по истечении некоторого вре-мени после подачи такого возмущения, когда затухнут все движения, оп-ределяемые переходным процессом, на выходе звена или системы уста-новится также гармоническое изменение выходной величины y с той же частотой ω, которую имеет входная величина, но с иными амплитудой x и смещением фазы на величину φ. Амплитуда и фаза на выходе при прочих равных условиях будут зависеть от частоты возмущающего воздействия. По этим характеристикам можно судить о динамических свойствах не только звеньев, но и сложных замкнутых САУ.

K 1 (j ω )

K 2 (j ω )

Kn(j ω )

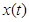Рис. 23. Линейная САУ под воздействием гармонического возмущения

Для линейных систем справедлив принцип суперпозиции: реакция сис-темы на несколько одновременно действующих входных воздействий рав-

на сумме реакций на каждое воздействие в отдельности. Это позволяет ог-раничиться изучением систем только с одним входом.

Рассмотрим несколько понятий, связанных с частотными характерис-тиками. Периодическое гармоническое возмущение в векторной форме может быть записано так: , где . Последнее выражение представляет собой единичный вектор, у которого cosω t – вещественная часть;sinω t – мнимая часть; X – амплитуда; ω t – фа-зовое состояние процесса.

По истечении переходного процесса на выходе разомкнутой системы установятся вынужденные периодические колебания, определяемые выра-жением

.

По определению комплексный коэффициент усиления K(j ω ) получают из передаточной функции W(p) при подстановке в неё вместо p→j ω

K(j ω )=y(t)/x(t)=Ye^{j(ωt+ φ )}/Xe^{j ω t} =K( ω )e^{j φ}.

Здесь K (ω) =Y/X зависит от частоты так же, как от частоты зависит и величина φ.

Так как x(t) и y(t) – векторы, то их можно изобразить на комплексной плоскости. Вектор будет изображен в виде отрезка, длина которого равна амплитуде (рис. 24): 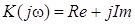, tgφ =Im/Re, где Re – действительная часть; Im – мнимая часть. Таким образом, комплексный коэффициент уси-ления есть векторная величина, модуль которой 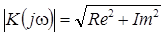, а фа-за отсчитывается от действительной оси.

При непрерывном изменении частоты происходит изменение модуля и фазы вектора. Конец вектора описывает на комплексной плоскости некото-рую кривую, называемую годографом. Годограф - геометрическое место точек конца вектора комплексного коэффициента усиления на комплекс-ной плоскости при изменении частоты от 0 до ∞. Значение частот отклады-вается непосредственно на годографе, который, таким образом, является амплитудно-фазочастотной характеристикой. Для определения модуля и фазы комплексного коэффициента усиления на заданной частоте следует соответствующую точку годографа соединить прямой с началом коорди-нат. Длина полученного отрезка соответствует в определенном масштабе

модулю, а фаза определяется углом, образованным этой прямой и положи-тельной полуосью действительных величин (рис. 25).

Рис. 24. Характеристики комплексного коэффициента усиления

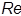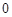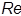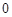Рис. 25. Примеры годографов разомкнутых САУ

При расчетах систем пользуются логарифмической амплитудно-частот-ной (ЛАЧХ) и логарифмической фазочастотной (ЛФЧХ) характеристика-ми. По горизонтальной оси откладывают частоту в логарифмическом мас-штабе, что позволяет изобразить на заданном отрезке значительный диапа-зон частот. Это наиболее удобная форма представления частотных харак-теристик для решения задач анализа и синтеза систем. Рассмотрим амп-литудно-фазовую характеристику . Прологарифмируем ее: ln K(j ω ) = ln K( ω )+j φ(ω). На практике используют десятичные логариф-мы lg K(j ω ) = lg K( ω )+j , так как ln N = lg N/ lg e = lg N/ 0,4329 = 2,3lg N.

Рассмотрим координатную систему для такого представления (рис. 26). По оси абсцисс откладываем величину lg ω. Вводим две единицы измере-ния: декаду, октаву. Декада – длина отрезка по оси абсцисс, соответствую-щая десятикратному изменению частоты. Число декад n _д = lgω_в/ω_н , где ω_в – крайняя высокая частота рассматриваемого диапазона; ω_н– крайняя нижняя частота.

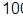
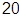
Рис. 26. Координатная система для построения

ЛАЧХ и ЛФЧХ

Например частотный диапазон от ω_н=1 с^-1 до ω_в=10000 с^-1 содержит че-тыре декады, так как lg 10⁴ = 4. Первая декада – от 1 до 10 с^-1; вторая – от

10 до 100 с^-1; третья – от 100 до 1000 с^-1 и т.д. Октава – длина отрезка по оси абсцисс, соответствующая двухкратному изменению частоты. В одной декаде содержится 3,32 октавы. Декадный интервал применяют чаще.

Фазу обычно откладывают по оси ординат в угловых градусах или в ра-дианах. Ординатой амплитудно-частотной характеристики является не величина lg K( ω ), а пропорциональная ей величина L( ω ), в децибелах, L( ω ) = 20lg K( ω ) (шкала равномерная). Точка пересечения с осью абсцисс соответствует K( ω ) = 1.

Использование логарифмического масштаба при построении ЛАЧХ обусловлено не столько значительными изменениями модуля комплексно-го коэффициента усиления, сколько возможностью осуществления графи-ческих методов расчета. При расчетах САУ часто приходится иметь дело с произведением коэффициентов усиления, а так как логарифм произведе-ния равен сумме логарифмов, то при графических расчетах для получения произведения нескольких значений весьма удобно осуществить сложение их логарифмов. Удобство логарифмического масштаба по оси ординат в том, что на одном графике можно представить значения, отличающиеся на несколько порядков.

Временные характеристики

Они – важные характеристики САУ. Это переходные и импульсные переходные функции и их графики. В реальных условиях входные сигналы могут иметь произвольный характер. Для исследования динамических свойств элементов и систем следует выбрать такие типовые возмущения, которые по возможности близко отражали бы наиболее существенные осо-бенности реальных возмущений.

В теории САУ для определения динамических свойств звеньев (систе-мы) в качестве входного сигнала применяют следующие типовые функции (рис. 27): единичный скачок (ступенчатая функция (рис. 27, а), например подключение напряжения к звену или системе, начало обработки на стан-ке, возмущения в виде ударов в механических системах и др.); единичный импульс (рис. 27, б) (как правило, шумы, помехи); гармонический сигнал (рис. 27, в); степенные функции времени (линейные, квадратичные и др.) (рис. 27, г).

Переходная функция системы (звена) – функция, описывающая измене-ние выходной величины системы (звена), когда на ее вход подается еди-ничное ступенчатое воздействие при нулевых начальных условиях. Пере-ходную функцию обычно обозначают как h(t). Иначе, переходная функция

h(t) – функция, описывающая реакцию системы (звена) на единичное сту-пенчатое воздействие при нулевых начальных условиях. График переход-ной функции называют переходной характеристикой.

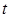
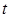
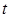
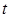
Рис. 27. Типовые функции входного сигнала

Импульсная переходная функция системы (звена) – функция, описываю-щая реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях. График импульсной переходной функции называют импульсной переходной характеристикой.

Физически единичный импульс можно представить как очень узкий им-пульс единичной площади.

Переходную функцию принято вписывать в прямоугольник, изобража-ющий звено.