В общем виде дифференциальное уравнение звена САУ имеет вид:
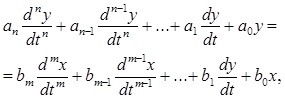(6)
где y – выходная величина (в отклонениях от состояния равновесия); x – выходная величина звена (в отклонениях от состояния равновесия); an, an- 1 ,…, a 1, a 0, bm,bm- 1 ,…, b 1, b 0 – постоянные коэффициенты, определяемые конструктивными особенностями и параметрами звена.
Так как аналитическое решение дифференциального уравнения в общем случае является трудоемкой задачей, то в современной теории управления широко используют средства описания динамических свойств системы че-рез преобразование Лапласа, что удобнее для практического применения.
Основанием для преобразования служит то обстоятельство, что оно су-щественно облегчает исследование сложных систем, при замене диффе-ренциальных уравнений алгебраическими. В частности, при решении диф-ференциальных уравнений систем преобразование Лапласа позволяет лег-ко учитывать начальные условия и избежать сложных выкладок, связан-ных с вычислением постоянных интегрирования.
Если в уравнение (6), содержащие функции времени y(t) и x(t), ввести функции y(p) и x(p) комплексного переменного p, поставив условие, что эти функции связаны зависимостями
, 
, (7)
то оказывается, что дифференциальное уравнение, содержащее функции y(t) и x(t), равносильно линейному алгебраическому уравнению, содержа-щему функции y(p) и x(p):
(8)
Такой переход от дифференциального уравнения к однозначно соответ-ствующему ему алгебраическому уравнению называют преобразованием Лапласа, интеграл (7) – интегралом Лапласа, комплексное переменное p – оператором. Сообразно с этим алгебраическое уравнение (8) является за-писью исходного дифференциального уравнения (6) в операторной форме.
Функцию y(p) называют изображением функции y(t), а функцию y(t) – оригиналом функции y(p). Операция перехода от исходной функции y(t) к ее изображению y(p) (нахождение изображения по оригиналу) называют прямым преобразованием Лапласа. Математически прямое преобразование Лапласа записывают условно с помощью символа L[y(t)] = y(p). Операцию перехода от изображения y(p) к искомой функции y(t) (нахождение ориги-нала по изображению) называют обратным преобразованием Лапласа. Ма-тематически обратное преобразование Лапласа записывается с помощью символа L- 1 [y(p)] = y(t). Практически переход от дифференциального урав-нения к алгебраическому происходит без каких-либо вычислений.
Если сравнить уравнения (1) и (3), то нетрудно заметить, что формально переход дифференциального уравнения к алгебраическому операторному уравнению при нулевых начальных условиях получают путем замены сим-
волов дифференцирования оригиналов функций 
,…, 
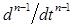соответственно символами pn, pn- 1 ,…, p и функций y(t) – их изображе-ниями y(p). С оператором p можно, как и с другими членами алгебраичес-кого уравнения, производить различные действия (умножение, деление, вынесение за скобки и т.д.). Возможность записи дифференциального уравнения в операторной алгебраической форме значительно упрощает все расчеты.
Каждое звено САУ в общем случае описывают дифференциальным уравнением вида (6). Следовательно, при вводе дифференциального урав-нения системы в целом необходимо совместно решить несколько диффе-ренциальных уравнений высших порядков. Запись дифференциального уравнения в операторной форме позволяет свести задачу к решению сис-темы алгебраических уравнений. Определив из алгебраических уравнений изображение y(p) искомой функции y(t), определяющей переходный про-цесс в системе, находим эту функцию, пользуясь таблицами формул изоб-ражений функций, или графическим путем. Кроме того, запись дифферен-циальных уравнений звеньев системы в операторной форме дает возмож-ность ввести удобное понятие передаточной функции, характеризующей звено системы. С помощью передаточных функций расчет САУ еще более упрощается и становится доступным широкому кругу инженеров, без не-обходимости применения сложного математического аппарата.
Вынесем в уравнении (8) y(p) и x(p) за скобки и получим
(anpn+an- 1 pn- 1 +…+a 1 p+a 0 )y(p)=(bmpm+bm- 1 pm- 1 +…+b 1 p+b 0 )x(p).
Определим из уравнения (4) отношение изображения выходной вели-чины к изображению входной
.
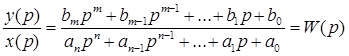Отношение W(p) изображения выходной величины системы к изобра-жению его входной величины называют передаточной функцией системы. Соответственно отношение изображения выходной величины звена к изоб-ражению его входной величины называют передаточной функцией звена. Передаточная функция W(p) является дробно-рациональной функцией опе-ратора p:
W(p)=Q(p)/P(p),
где P(p) = anpn + an- 1 pn- 1 +…+ a 1 p + a 0 – оператор левой части дифференци-ального уравнения; Q(p) =bmpm + bm- 1 pm- 1 +…+ b 1 p + b 0 – оператор правой части уравнения.
Из уравнения (2) следует, что передаточная функция звена системы W(p) и изображение его выходной величины определяют изображение вы-ходной величины y(p)=W(p)x(p).
При рассмотрении типовых динамических звеньев часто встречаются функциональные зависимости, приведенные на рис. 22.
 |  |
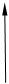
Рис. 22. Типовые функциональные зависимости:
а – единичная функция; б – экспонента вида 
;
в – экспонента вида (1– ); г – непрерывно
возрастающая функция
Определим лапласово изображение единой функции x(t) = 1:
.
Изображение экспоненты вида x(t) = e-t/T:
.
Изображение экспоненты вида x(t)= 1 -e-t/T:
.
Изображение непрерывно возрастающей функции x(t)=Kt:
.