Тема. Абсолютные, относительные и средние величины.

План.

1. Понятие об абсолютных и относительных величинах как категориях статистической науки.

2. Формы и виды относительных величин.

3. Средние величины и показатели вариации.

 

1. Понятие об абсолютных и относительных величинах как категориях статистической науки.

В результате наблюдения и сводки статистических данных получают обобщающие статистические показатели.

Абсолютные величины характеризуют размер изучаемых явлений и представляют собой именованные числа, т.е. имеют какую-либо единицу измерения (единицы веса, меры, объема, протяженности, площади и т.д.).

Абсолютные величины представляют собой именованные числа, т.е. имеют какую-либо единицу измерения (единицы веса, меры, объема, протяженности, площади и т.д.).

Все единицы измерения можно объединить в группы:

- натуральные единицы измерения – выражаются в физических мерах веса, длины, объема и т.д.

- стоимостные единицы измерения – выражаются в рублях, тыс. рублей и др. Применяются для оценки явлений в денежном выражении.

- условно-натуральные единицы измерения – применяются при производстве однородной, но неодинаковой продукции. Сущность этого метода состоит в том, что единица одной разновидности продукции берется за условную (эталон), а все другие переводятся в условные единицы путем умножения их количества в натуральном выражении на переводные коэффициенты.

- трудовые единицы измерения – характеризуют использование трудовых ресурсов или затраты труда: человеко-часы, человеко-дни.

Абсолютные величины являются суммарными показателями и применяются в зависимости от особенностей, характера изучаемых явлений.

В анализе и планировании хозяйственной деятельности кроме абсолютных величин применяются относительные величины.

2. Формы и виды относительных величин.

Относительные величины являются обобщающими показателями, они дают возможность сравнивать между собой абсолютные величины, сопоставлять разноименные показатели.

Относительная величина – это величина, которая получается путем деления одной абсолютной величины на другую. При расчете относительных величин следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе – показатель с которым производится сравнение, принимаемый за основание или базу сравнения.

Относительные величины могут выражаться в следующих формах:

1. Форма коэффициента – если база сравнения принимается за единицу. Рассчитываемый показатель покажет во сколько раз сравниваемая величина больше или меньше основания.

2. Форма процентов (%) – если база сравнения принимается за 100. Если из полученного показателя вычесть 100%, можно сказать, на сколько процентов сравниваемая величина больше или меньше основания.

3. Форма промилле (‰) – если база сравнения принимается за 1000. Используется, например, при определении демографических коэффициентов.

4. Форма продецимиле - если база сравнения принимается за 10000.

Виды относительных величин.

Относительная величина планового задания представляет собой отношение планового уровня показателя текущего года к его уровню в прошлом году или к среднему за три-пять предыдущих лет:

Пример. Оборот произведенной продукции коммерческой фирмой в базисном году составил 2,0 млрд. руб. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считает реальным в следующем году довести объем выпуска продукции до 2,8 млрд.руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 140% (2,8/2,0х100 = 140%).

Относительная величина выполнения плана - это отношение между фактическим и плановым уровнем показателя, выраженное обычно в процентах:

Пример. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считало реальным в отчетном году довести выпуск продукции до 2,8 млрд. руб. Фактический выпуск продукции в отчетном году составил 2,6 млрд. руб.. Относительный показатель выполнения плана, определяемый как отношение фактически достигнутой величины к ранее планировавшейся, составит 92,9% (2,6/2,8 х 100 = 92,9%).

Относительные величины динамики – используют д ля характеристики изменения показателей за какой-либо промежуток времени.Их определяют путем деления величины показателя текущего периода на его уровень в предыдущем периоде (месяце, квартале, году). Относительные величины динамики могут быть базисными и цепными. В первом случае каждый следующий уровень динамического ряда сравнивается с базисным годом, а в другом - каждый следующий год относится к предыдущему:

Рассчитанная таким образом величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный). Относительная величина динамики может выражаться не только в процентной, но и в коэффициентной форме, он называется коэффициентом роста, при умножении этого коэффициента на 100% получают темп роста.

Пример. Объем произведенной продукции коммерческой фирмы в базисном году составил 2,0 млрд. руб., а в отчетном году - 2,6 млрд. руб. Тогда относительный показатель динамики, определяемый как отношение фактически достигнутой в отчетном году величины к фактически достигнутой в базисном году, составит 130% (2,6/2,0х 100=130%).

Между относительными показателями планового задания, выполнения плана и динамики существует следующая взаимосвязь:

О.В.ПЗ х О.В.ВП = О.В.Д.

В нашем примере: 1,40 х 0,929 = 1,3.

Основываясь на этой взаимосвязи, по любым двум известным величинам при необходимости всегда можно определить третью, неизвестную величину.

Относительная величина структуры - это относительная доля (удельный вес) части в общем, выраженная в процентах или коэффициентах:

Относительный показатель структуры выражается в долях единицы или в процентах.

Пример. Из общего объема произведенной в отчетном году продукции (2,6 млрд. руб.), экспорт составляет 0,7 млрд. руб. Следовательно, доля экспорта в общем объеме реализации, произведенной продукции составляет 26,92% (0,7/2,6х100= 26,92%). Доля продукции, реализуемой на внутреннем рынке составляет 73,08% ((2,6-0,7)/2,6х100=73,08%). Сумма удельных весов должна составлять 100%

Относительная величина сравнения - используется для сравнения одноименных величин, имеющих разное значение.

Уровень расходов = ; Рентабельность =

Предприятие 1: сумма расходов 25,6 тыс. руб.., уровень расходов 18,55%.

Предприятие 2: сумма расходов 73,2 тыс. руб.., уровень расходов 16,21%.

В территориально-пространственных сравнениях соотносят одноименные показатели, которые характеризуют разные объекты (предприятия, отрасли) или территории (города, регионы, страны)) и имеют одинаковую часовую определенность. Интерпретация этих величин зависит от базы сравнения.

Пример. В стране А производство ВВП на душу населения составило 3522 дол США, а в стране Б – 5280. Если принять за базу сравнения страну А, можно сказать, что в стране Б ВВП на душу населения в 1,5 раза выше (5280/3522=1,5). Если базой сравнения принять страну Б, то в стране А ВВП на душу населения составит 2/3 уровня страны Б (3522/5280=0,67).

Базой сравнения может выступать определенное эталонное значение показателя (норматив, стандарт).

Пример. Рациональная норма питания детей в возрасте 1-3 года предусматривает потребление 1540 ккал и 53 г белка. По данным исследований в регионе фактическое потребление составляет 1370 ккал и 46 г белка.

Фактическое потребление отклоняется от рациональной нормы по калорийности питания на 11% (1370/1540%=89,0%), по белку на 13,2% (46/53%=86,8%)

Относительные величины координации представляют собой соотношение частей целого между собой, является одной из разновидностей показателей сравнения.

При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической точки зрения. В результате получают, сколько единиц каждой структурной части приходится на 1 единицу (иногда на 100, 1000 и т. д. единиц) базисной структурной части.

Пример. По данным переписи 2001 г. численность населения АР Крым составила 2033,7 тыс.чел., в том числе:

- мужчины – 937,6 тыс.чел., женщины – 1096,1 тыс.чел.;

- городское население – 1274,3 тыс.чел., сельское население – 759,4 тыс.чел.

Определить:

1. Соотношение женщин и мужчин на 100 человек;

2. Соотношение городского населения и жителей сельской местности на 100 человек.

Решение.

1. Сколько женщин приходится на 100 мужчин 1096,1/937,6х100=116,9≈117 чел.;

Сколько мужчин приходится на 100 женщин = 937,6/1096,1х100=85,5≈86 чел.

2. Сколько жителей сельской местности приходится на 100 человек городского населения 759,4/1274,3х100=59,6≈60 человек

Сколько городских жителей приходится на 100 жителей сельской местности 1274,3/759,4х100=167,8≈168 человек.

Относительными величинами интенсивности называются те, которые характеризуют степень распространенности, развития какого-либо явления в соответствующей присущей ему среде.

Этот показатель выражаться в процентах, промилле или быть именованной величиной. Например, степень заболеваемости населения, процент рабочих высшей квалификации и т.д.

Пример. Розничный товарооборот торгового предприятия за месяц в отчетном году составил 4726 тыс. руб. Численность обслуживаемого населения 5992 чел.

Решение.

О.В. интенсивности (товарооборот на 1 человека = 4726/5992=788,72 руб.

 

3. Средние величины и показатели вариации.

Средней величиной в статистике называется обобщающий показа­тель, характеризующий типичный уровень явления в конкретных ус­ловиях места и времени, отражающий величину варьирующего при­знака в расчете на единицу качественно однородной совокупности.

В статистике используются следующие виды средних величин:

Средняя арифметическая является наиболее распространенным видом средних величин. Бывает простая и взвешенная.

Средняя арифметическая простая применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных её единиц.

Пример.

Площадь 10 магазинов составила (м²): 60, 50, 70, 70, 60, 70, 80, 80, 70, 60.

Рассчитать среднюю площадь одного магазина.

Решение.

х₁, х₂…х_n - индивидуальные значения признака;

n – число единиц совокупности.

Средняя арифметическая простая равна сумме вариант деленной на их количество и рассчитывается по одному ряду чисел.

Приведенные в предыдущем примере данные можно объединить в однородные группы:

Площадь магазинов, м2
Количество магазинов, ед.

В этом случае варианты повторяются несколько раз, или, как говорят, имеют разный вес. Средняя в этом случае называется средняя арифметическая взвешенная и рассчитывается по формуле:

,

где х₁, х₂…х_n - индивидуальные значения признака;

f_1, f_2,… f_n – веса (частоты повторения одинаковых признаков).

Умножение вариант на частоты в статистике называется взвешиванием, поэтому и средняя арифметическая взвешенная.

Средняя арифметическая взвешенная рассчитывается по двум рядам чисел. За ряд вариант (х) принимается тот ряд, среднюю которого надо найти, ряд весов (f) – показывает сколько раз повторяются варианты.

Средняя арифметическая взвешенная равна сумме произведений вариант на соответствующие им веса, деленная на сумму весов.

Среднюю величину можно рассчитать не только в дискретном, но и в интервальном ряду.

Если значения признака, по которому надо рассчитать среднюю величину, заданы в виде интервалов, то при расчете средней арифметической в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.

Средняя арифметическая обладает рядом свойств, позволяют сократить время на её расчет.

Свойства средней арифметической:

1. Нулевое свойство средней величины заключается в том, что сумма отклонений вариант от их средней арифметической величины, равна нулю.

2. Если все варианты уменьшить (или увеличить) на одно и то же число, то средняя арифметическая из этих вариантов уменьшится (или увеличиться) на то же самое число.

3. Если все варианты уменьшить (или увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (или увеличиться) во столько же раз.

4. Если все веса средней одинаково уменьшить (или увеличить) в несколько раз, средняя арифметическая не измениться.

Средняя гармоническая применяется в тех случаях, когда веса (частоты) не приводятся непосредственно, а входят сомножителем в один из имеющихся показателей. Средняя гармоническая является обратной средней арифметической, бывает простой и взвешенной.

Пример. Определить среднюю цену 1 кг товара.

Магазины	Цена за единицу товара, руб.	Стоимость проданного товара, руб.
№ 1	64,0	8320,0
№ 2	78,0	9360,0

В тех случаях, когда веса равны единице применяется средняя гармоническая простая, рассчитываемая по формуле:

где - отдельные варианты обратного признака, встречающиеся по одному ряду;

n – число вариантов.

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, т.е. характеризуют средний коэффициент роста.

,

где n – число вариантов;

П – знак произведения.

Средняя квадратическая и средняя кубическая используются для расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения, бывают простые и взвешенные.

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратическая взвешенная:

Средняя кубическая рассчитывается аналогично.

 

 

Средняя кубическая простая:

Средняя кубическая взвешенная:

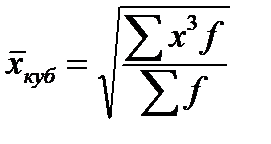
Средняя хронологическая применяется при расчете средних товарных запасов в торговой организации и рассчитывается по формуле:

Пример.

Остатки товаров на складе за 1 квартал составили:

на 1.01 -348,0 тыс.руб.

на 1.02 – 308,0 тыс.руб.

на 1.03 – 348,0 тыс.руб.

на1.04. – 286,0 тыс.руб.

Определить средний товарный запас за 1 квартал.

Решение.

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.Мода (М_о) – это варианта у которой наибольшая частота, т.е. чаще всего встречающаяся частота ряда распределения. В отличие от других средних величин, мода является величиной конкретной.Медиана (М_е) – это варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от неё находится одинаковое количество единиц совокупности.

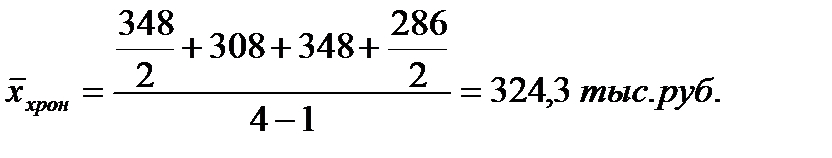
Средние величины дают обобщающую характеристику совокупности по варьирующим признакам. В средней величине не проявляется степень колеблемости отдельных значений признака (вариант) вокруг среднего уровня. Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.

Термин «вариация» произошел от латинского слова variatio, что означает – изменение, колеблемость, различие.

Для измерения вариации признака в совокупности в статистике используют ряд обобщающих показателей:

- размах вариации рассчитывается как разность между наибольшим и наименьшим значениями варьирующего признака:

- дисперсия (средний квадрат отклонений) – это средний квадрат отклонений вариантов от средней величины и определяется как средняя из отклонений, возведенных в квадрат.

Дисперсия бывает:

простая

взвешенная

- среднее квадратическое отклонение или корень квадратный из дисперсии (среднего квадрата отклонений):

простое

взвешенное

или

В статистической практике часто возникает необходимость сравнения вариаций разных признаков. Для такого сравнения используется относительный показатель вариации – коэффициент вариации.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

Пример. Определить показатели вариации по данным дискретного ряда.

Ряд	Отклонение вариант от средней	Квадраты отклонений
	-13,6 -8,6 -2,6 8,4 16,4	184,96 73,96 6,76 70,56 268,96
	-	605,2

Решение.

1. Средняя арифметическая

2. Отклонение вариант от средней 7-20,6 = -13,6 ед. и т.д.

3. Квадраты отклонений (-13,6)² = 184,96 ед. и т.д.

4. Дисперсия (средний квадрат отклонений)

5. Среднее квадратическое отклонение =11,3 ед.

Отдельные варианты отклоняются от средней в одном случае на большую величину, в другом - на меньшую, а в среднем это отклонение составляет 11,3 ед. Простое среднее квадратическое отклонение выражается в тех же единицах измерения, что и варианты.

6. Коэффициент вариации

Коэффициент вариации используется для сравнительной оценки вариации единиц совокупности, а так же как характеристика однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.

 

Литература.

Статистика [Текст]: учебник для студентов учреждений СПО / В. С. Мхитарян, Т. А. Дуброва, В. Г. Минашкин; ред. В. С. Мхитарян. – 14-е изд., стер. – М.: Академия, 2015, (97-106, 109-127).