ПОСТУЛАТЫСТО.
,
где m 0 – масса покоя, с=3.108м/с.
Из самой формулы очевидно, что рост массы в обычных условиях незначителен, то есть законы Ньютона можно считать приближенно выполнимыми при условии, что 
I постулат – (принцип относительности) все физические явления (законы) в ИСО при одинаковых начальных условиях протекают одинаково.
II постулат: (принцип инвариантности скорости света в вакууме). Скорость света в вакууме не зависит от скорости движения источника света и наблюдателя и одинакова во всех инерциальных системах отсчёта (с = 3 . 10 8м/с = const).
Скорость света в вакууме – абсолютна, константа.
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА.
Преобразования Лоренца – это преобразования четырех координат.
Рассмотрим две ИСО, из которых K- условно неподвижна (x,y,z) и K’- движущаяся относительно К со 
(рис.2). Пусть 
,x,x,- сонаправлены.
 | |||
 | |||
Пусть в начальный момент 
начала координат совпадают 
Рассмотрим некоторую точку А пространства до которой дошла электромагнитная волна вдоль оси x.
А К: x=ct – расстояние пройденное волной.
А К,:x,=ct ,
x-x,=с(t-t,).
Очевидно, что x 
x, 
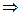t t,.
Таким образом из-за того, что c=const 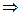время будет разное в этих СО.
Найдем преобразование координат.
Рассмотрим точку 0 ’, в системе K’ координата этой точки равна нулю.
0 ’ K’: x’ = 0 (1).
K:x = vt или x – vt = 0 (2).
Уравнения (1) и (2) отличаются друг от друга некоторым коэффициентом a.
Т.о. 
(3).
a - коэффициент с точностью до которого равны данные выражения.
Теперь запишем выражение для абсцисс точки О.
О K: x = 0
K’: 
(так как точка О лежит в отрицательной части абсцисс) или 
.
Проведя рассуждения, аналогичные приведённым выше, можно записать:
(4)
Перемножим (3) и (4), подставив выражения для x и x’.
(5)
где 
.
Найденное значение a подставим в (3) и (4).
(6)
(7)
Для определения формулы преобразования времени при переходе от одной ИСО к другой запишем формулу (7) в виде:
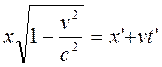
Подставим x’ из (6)
Освободимся от знаменателя
(8)
Аналогично можно получить
(9)
(10) 
(11)
Анализируя уравнения, делаем выводы:
1. В формулы преобразований равноправно входят координаты пространства и времени.
2. Формулы преобразований симметричны относительно обеих систем, т.е. отличаются только знаком относительной скорости u.
3. При v<<c преобразование Лоренца переходит в преобразование координат Галилея:
4. При v>c выражение для координат и времени становится мнимым. Это находится в соответствии с тем, что движение со скоростью большей скорости света в вакууме, невозможно.
5. Нельзя пользоваться ИСО, движущейся со скоростью равной с, т.к. при v = c знаменатели в формулах обращаются в нуль. (
и формулы преобразования теряют смысл).
ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ.
Рассмотрим этот вопрос для частного случая, когда материальная точка движется в системе K параллельно оси x со скоростью u. В этом случае проекции скорости материальной точки в системе K будут равны:
Проекции скорости этой материальной точки в системе K’ будут:
Так как 
то 
На основании преобразования Лоренца
; 
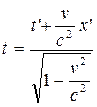
имеем:
(1)
(2)
Разделив уравнение (1) на (2) получим
(3)
Аналогично, с учетом знака относительной скорости v, можно получить
(4)
Соотношения (3) и (4) определяют релятивистский закон сложения скоростей для рассмотренного частного случая движения материальной точки.
Пример:
Пусть объект (фотон 
) в системе K’ движется со скоростью 
. То из (3) следует, что
(!)
Этот результат не является удивительным, так как в основе преобразований Лоренца лежит постулат о постоянстве скорости света в вакууме.