Выборочным распределением (статистическим рядом) называют перечень вариант и соответствующих им частот или относительных частот.
Для наглядности статистический ряд представляют графически в виде полигонов и гистограмм частот.
Полигон, как правило, служит для изображения дискретного статистического ряда и представляет собой ломаную линию, в которой концы отрезков прямой имеют координаты 
, 
,..., 
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 
, 
,..., 
.
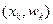Гистограмма (статистический аналог плотности) служит для изображения интервальных (непрерывных) статистических рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака и высотами, равными частотам. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения. Для построения гистограммы используют метод группировки.
4. Числовые характеристики выборочного распределения. Выборочное среднее и его свойства.
Выборочное (эмпирическое) среднее — это приближение теоретического среднего распределения, основанное на выборке из него.
Пусть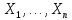 
—выборка из распределения вероятности, определённая на некотором вероятностном пространстве (Ω,F,P). Тогда её выборочным средним называется случайная величина.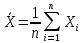 
Свойства выборочного среднего:
Пусть 
—выборочная функция распределения данной выборки. Тогда для любого фиксированного ω функция 
является функцией дискретного распределения. Тогда математическое ожидание этого распределения равно 
Выборочное среднее — несмещённая оценка теоретического среднего:
Выборочное среднее — сильно состоятельная оценка теоретического среднего:
почти наверное при 
.
Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин 
конечна и ненулевая, то есть 
Тогда 
по распределению при ,
где 
— нормальное распределение со средним 0 и дисперсией 
.
Выборочное среднее из нормальной выборки — эффективная оценка её среднего.
5. Числовые характеристики выборочного распределения. Выборочная дисперсия и ее свойства.
Выборочная дисперсия — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии.
Пусть 
— выборка из распределения вероятности. Тогда Выборочная дисперсия — это случайная величина
,
Несмещённая (исправленная) дисперсия — это случайная величина
.
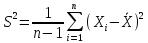Свойства выборочных дисперсий:
Пусть —выборочная функция распределения данной выборки. Тогда для любого фиксированного 
функция является функцией дискретного распределения. Дисперсия этого распределения равна 
.
Обе выборочные дисперсии являются состоятельными оценками теоретической дисперсии. Если, 
И 
,
где 
обозначает сходимость по вероятности.
Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённой:
,И 
Выборочная дисперсия нормального распределения (задаётся ф-цие Гаусса) имеет распределение хи-квадрат.
