Модой называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности.
Если распределение равномерное, где все варианты встречаются одинаково част, то говорят, что ряд не имеет моды, или, иначе, что все варианты одинаково модальны. Могут быть случаи, когда две варианты встречаются одинаково часто. Тогда говорят, что распределение бимодально. Для нахождения медианы необходимо сумму частот разделить пополам и к полученному результату прибавить 0,5. Если в ряду имеется четное количество частот.
Расчет моды в интервальном вариационном ряду. В моде и медиане не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Если имеются все значения признака, то не требуется проводить расчеты для определения моды и медианы. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам.
Расчет медианы в интервальном вариационном ряду. Для исчисления медианы сначала необходимо определить интервал, в котором она находится (медианный интервал). Это интервал, кумулятивная частота которого будет превышать половину суммы частот.
Формула для исчисления медианы для интервального вариационного ряда будет иметь вид: Ме= ХМе+IМе *(∑f/2-S Ме-1) / fМе
Где ХМе- начальное значение медианного интервала;
IМе- величина медианного интервала;
(∑f – сумма частот ряда(численность ряда);
S Ме-1 – сумма накопленных частот в интервалах, предшествующих медианному;
fМе- частота медианного интервала.
8. Числовые характеристики выборочного распределения. Начальные и центральные моменты.
1. Центральный момент 1-го порядка равен нулю: 
.
2. Центральный момент 2-го порядка - это дисперсия случайной величины: 
.
3. Центральный момент 3-го порядка служит характеристикой асимметрии распределения.
Если распределение случайной величины 
- симметричное, то 
.
Число, которое находится по формуле 
, называется коэффициентом асимметрии.
4. Центральный момент 4-го порядка служит характеристикой "островершинности" или "плосковершинности"
распределения.
9. Понятие об оценке параметров. Несмещенность оценки.
Несмещенность оценки означает, что при ее использовании мы не получаем систематической ошибки, и только при наличии этого свойства оценки могут иметь практическую значимость.
Следовательно, при большом числе выборочных оцениваний остатки не будут накапливаться и найденный параметр можно рассматривать как среднее значение из возможно большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
10. Понятие об оценке параметров. Состоятельность оценки.
Состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений. Состоятельность обычно рассматривается как самое важное свойство оценки (это минимальное требование, предъявляемое к любой оценке).
Признаком несостоятельности оценки является резкое изменение коэффициентов регрессии при изменении объема выборки.
11. Понятие об оценке параметров. Эффективность оценки.
Эффективная оценка является наилучшей в смысле минимума среднеквадратичного отклонения. Оценки, полученные методом наименьших квадратов при выполнении всех необходимых предпосылок (гипотез), являются эффективными.
12. Методы нахождения оценок параметров. Метод моментов.
13. Методы нахождения оценок параметров. Метод максимального правдоподобия
.
14. Методы нахождения оценок параметров. Метод наименьших квадратов.
15. Понятие об интервальной оценке параметров. Доверительная вероятность и доверительный интервал.
Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений используется распределение вероятностей Стьюдента.
 |
Нижняя граница интервала
 |
Верхняя граница интервала
 |
16. Интервальная оценка генеральной доли.
Рассмотрим случай, когда объём выборки достаточно большой (n > 30), а генеральная случайная величина распределена по биномиальному закону. Требуется оценить вероятность p наступления некоторого события А в каждом испытании по результатам n наблюдений.
При большом числе испытаний частость (выборочная доля) события А 
имеет приближённо нормальное распределение с параметрами 
, которые будем заменять выборочными значениями 
и 
для противоположного события 
. Тогда имеем:
(10)
Здесь 
- средняя квадратическая ошибка при оценке генеральной доли. Вычисляется в зависимости от способа образования выборки.
Повторная: 
Бесповторная: 
Для определения необходимого объёма выборки при фиксированной предельной ошибке 
, нетрудно получить формулы:
Повторная: 
Бесповторная: 
17. Интервальная оценка генеральной средней.
При достаточно большом объеме выборки можно сделать вполне надежные заключения о генеральной средней. Однако на практике часто имеют дело с выборками небольшого объема (п < 30). В этом случае в выражении доверительного интервала точность оценки определяется по следующей формуле:
где t — параметр, называемый коэффициентом Стьюдента (его находят из распределения Стьюдента; оно здесь не рассматривается), который зависит не только от доверительной вероятности р, но и от объема выборки п.
Запишем неравенство, подставив в него выражение 
:
18. Интервальная оценка генеральной дисперсии.
Эффективной оценкой дисперсии в этом случае является
.
Используются два варианта интервальной оценки для σ2 (σ).
1. Основу первого варианта составляет
, которая имеет распределение χ2 с п степенями свободы независимо от значения параметра σ 2 и как функция параметра σ 2 > 0 непрерывна и строго монотонна.
Следовательно
,
где 
и 
двусторонние критические границы χ2-распределения с п степенями свободы.
Решая неравенство 
относительно σ 2, получим, что с вероятностью γ выполняется неравенство
,
и с такой же вероятностью выполняется неравенство
Числа и находят по прил. 1 k = n и соответственно при р = α /2 и р = 1 – α /2
2. Второй вариант предполагает нахождение интервальной оценки для σ при заданной надежности γ в виде
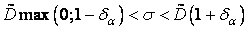
При δ α < 1 границы этой оценки симметричны относительно 
, и ошибка оценки , гарантируемая с вероятностью γ,
ε = δ α
19. Оценка объема выборки в случае генеральной средней.
Принципиальную возможность определения генеральной средней по данным простой случайной выборки доказывает теорема П.Л. Чебышева, также известная как «закон больших чисел». В приложении к выборочному методу неравенство. П.Л. Чебышева может быть сформулировано так: при неограниченном, увеличении числа независимых наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, сколь угодно близкой к единице, можно ожидать, что отклонение выборочной средней от генеральной средней будет сколь угодно мало.
При определении объёма выборки исследователь использует два основных статистических параметра: точность оценки и степень достоверности оценки.
Точность оценки – величина ошибки результата в абсолютном или относительном выражении. Степень достоверности оценки – вероятность того, что оценка соответствует истинному значению при установленной точности, т.е. вероятность гарантирующая результат.
20. Оценка объема выборки в случае генеральной доли.
Среднеквадратическая ошибка доли определяется (формула 1.7):
, (1.7)
где d – выборочная доля;
σp - среднеквадратическая ошибка доли;
n – объем выборки
В этом случае средним значением является генеральная доля, а среднеквадратическим отклонением – среднеквадратическая ошибка доли. Отсюда объем выборки определяется по формуле:
,
21. Понятие о проверке статистических гипотез. Общая схема их проверки.
Гипотеза - предположение, которое мы собираемся проверять
Статистическая гипотеза - предположение о распределении вероятностей на выборочном пространстве
Проверка статистических гипотез–
проверка соответствия характеристик выборки некоторым теоретическим (предполагаемым) значениям этих характеристик
Статистическая проверка гипотезы состоим из следующих этапов:
1) формулировка нулевой 
и альтернативной 
гипотез;
2) выбор соответствующего уровня значимости 
;
3) определение объёма выборки 
;
4) выбор статистики 
критерия 
для проверки гипотезы 
;
5) определение (по таблицам, по уровню значимости и по альтернативной гипотезе 
) критической области и области принятия гипотезы;
6) формулировка правила проверки гипотезы;
7) принятие статистического решения: если значения статистики не входит в критическую область, то принимается гипотеза 
и отвергается гипотеза 
, а если входит в критическую область, то отвергается гипотеза 
и принимается 
.
Результаты проверки статистической гипотезы нужно интерпретировать так: если приняли гипотезу , то можно считать ее доказанной, а если приняли гипотезу 
, то признали, что гипотеза не противоречит результатам наблюдений. Однако этим свойством наряду с могут обладать и другие гипотезы. Следует помнить, что, принимая гипотезу ,следует проводить ещё дополнительные исследования.
22. Понятие о проверке статистических гипотез. Значимость и мощность статистического критерия.
Уровень значимости - вероятность ошибочно отвергнуть гипотезу, когда она верна (т.е. вероятность ошибки первого рода); обозначается через a и заранее принимается достаточно малым
Мощность критерия - вероятность принять гипотезу, когда она верна (т.е. вероятность недопущения ошибки второго рода); обозначается через b и выбирается по возможности близким к 1 (при заранее заданном a)
Выберем событие А, условная вероятность которого при гипотезе Н0 меньше e. Если в эксперименте событие А произошло, то отвергаем гипотезу Н0 на уровне значимости e. Событие А - критическое для гипотезы Н0 или критерий для Н0.
Применяя юридическую терминологию, а - вероятность вынесения судом обвинительного приговора, когда на самом деле обвиняемый невиновен, р - вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен в совершении преступления. В ряде прикладных исследований ошибка первого рода а означает вероятность того, что предназначавшийся наблюдателю сигнал не будет им принят, а ошибка второго рода р -вероятность того, что наблюдатель примет ложный сигнал. Возможностью двойной ошибки (1-го и 2-го рода) проверка гипотез отличается от рассматриваемого выше интервального оценивания параметров, в котором имелась лишь одна возможность ошибки: получение доверительного интервала, который на самом деле не содержит оцениваемого параметра.
Вероятности ошибок /-го и 2-го рода (а и р) однозначно определяются выбором критической области.
23. Понятие о проверке статистических гипотез. Критическая точка и критическая область. Число степеней свободы.
Статистическим критерием называют выбранную случайную величину K, которая служит для проверки нулевой гипотезы. В качестве статистического критерия проверки гипотезы о равенстве нулю генерального среднего выбирают выборочное среднее, в качестве критерия проверки гипотезы о равенстве дисперсий двух совокупностей — отношение двух «исправленных» выборочных дисперсий.
После выбора критерия все возможные его значения можно разбить на два непересекающихся подмножества. Одно из подмножеств соответствует значениям критерия, когда нулевая гипотеза принимается, а другое подмножество — значениям критерия, когда она отвергается. Первое из подмножеств называется областью принятия гипотезы, а второе — критической областью. Следует предпочесть ту крит. область, при которой мощность критерия будет наибольшей; критическую область W следует выбирать так, чтобы вероятность попадания в нее статистики критерия О была минимальной и равной а, если верна нулевая гипотеза Н0, и максимальной в противоположном случае. Точки kкр, которые разделяют область принятия гипотезы от критической области, называются критическими точками. В зависимости от того, какая из конкурирующих гипотез выдвинута, критические области разделяются на правостороннюю, левостороннюю или двустороннюю. Правостороннюю критическую область определяют из равенства:
Для левосторонней критической области аналогично: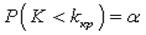 
.
В случае двусторонней критической области: 
В таблицах критических значений статистических критериев в общем количестве данных не учитывают те, которые можно вывести методом дедукции. Оставшиеся данные и составляют так называемое число степеней свободы (обозначается df, ν или k), т.е. то число данных из выборки, значения которых могут быть случайными.
24. Проверка гипотезы о равенстве средних двух генеральных совокупностей.
(По презентации: 1) Сначала Фишер-Снедекор 2) Если принимается, решаем по Стьюденту, чтобы ещё и средние сравнить)
Проверяется гипотеза 
: 
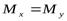, на уровне значимости 
. Конкурирующая гипотеза 
: 
Статистика для проверки:
; критическая область выбирается из условия 
. Если 
, то гипотеза 
не отвергается (не противоречит имеющимся наблюдениям).
Пример. Для проверки эффективности рекламной компании отобраны две группы магазинов. В первой, численностью 
, где проводилась рекламная компания, выборочная средняя составила 
проданных изделий, во второй группе, численностью 
, где рекламная компания не проводилась, выборочная средняя 
изделий. Установлено, что дисперсии продаж соответственно равны: 
. Выяснить: повлияла ли рекламная компания на объем продаж?
4 Нулевая гипотеза : 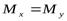, на уровне значимости 
. Конкурирующая гипотеза 
: 
. Фактическое значение критерия (статистики):
.
Критическое значения критерия находится из условия: 
. Так как 
, то нулевая гипотеза отвергается, что свидетельствует о влиянии рекламной компании на объем продаж.
25. Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей (ФИШЕР-СНЕДЕКОР).
Пусть имеются две нормально распределенных совокупности, дисперсии которых 
и 
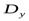. Проверяется гипотеза: 
: 
.
Конкурирующая гипотеза 
: 
.
Статистика для проверки:
;
1. Вычислить наблюдаемое значение критерия - отношение большей исправленной дисперсии к меньшей.
F набл = s 12 / s 22
2. Найти число степеней свободы исправленных дисперсий:
n 1 = n 1- 1 (большая)
n 2 = n 2-1 (меньшая)
3. По таблице критических точек распределения Фишера-Снедекора по уровню значимости a /2 (вдвое меньше заданного значения) и числам степеней свободы n 1 и n 2 найти F кр - критическую точку.
4. Если F набл< F кр - нет оснований отвергать нулевую гипотезу. Если F набл> F кр - нулевую гипотезу отвергают.
Пример. Проверяется точность изготовления детали на двух станках x и y. Извлечены выборки объемами 
и 
изделий соответственно. При этом рассчитаны исправленные выборочные дисперсии 
и 
. На уровне значимости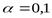 
проверить нулевую гипотезу 
: 
при конкурирующей гипотезе 
: 
.
4 
. 
По таблицам находим: 
. Так как 
, то нулевая гипотеза отвергается, т.е. станки не обеспечивают одинаковую точность.
26. Проверка гипотезы о равенстве нулю генерального коэффициента корреляции.
Даны два ряда выборочных значений X и Y. Полагая, что имеет место нормальное распределение двумерной генеральной совокупности, проверить нулевую гипотезу о равенстве нулюгенерального коэффициента корреляции.
 |
Т набл =
По таблице критических точек распределения Стьюдента, по заданному уровню значимости a и числу степеней свободы n = n-2 найти критическую точку двусторонней критической области t.
Если Т набл < t - нет оснований отвергнуть нулевую гипотезу. Иначе нулевая гипотеза отвергается
Если нулевая гипотеза принимается, то X и Y некоррелированы, в противном случае - коррелированы.
27. Проверка гипотезы о наличии связи (зависимости) двух случайных величин.
Объект исследований или испытаний может характеризоваться несколькими случайными величинами. Отдельные составляющие многомерной случайной величины могут быть как попарно независимыми, так и связанными друг с другом (зависимыми). Количественной мерой зависимости двух случайных величин x и y служит коэффициент корреляции:
Для независимых x,y r = 0. Располагая выборкой из n пар значений xi, yi, мы можем вычислить лишь оценку r или выборочный коэффициент корреляции
Плотность распределения выборочного коэффициента корреляции rn может быть рассчитана при условии, что x и y - независимы (т.е. r=0) и нормально распределены. У этого распределения один параметр - n.
Таким образом, rn может служить критерием проверки гипотезы: x и y независимы, или «связи между характеристиками объекта x и y – нет».
Проверка этой гипотезы может быть также осуществлена по t–критерию. Для этого надо вычислить экспериментальное значение
и при выбранном уровне значимости a по таблицам распределения Стьюдента при числе степеней свободы n –2 найти критическое значение t q, такое, что P{|t|>tq}=a.
28. Проверка гипотезы о виде закона распределения генеральной совокупности.
Проверка гипотезы о виде закона распределения производится с помощью специально подобранной случайной величины, называемой критерием согласия.
Имеется несколько критериев согласия: c 2 («хи-квадрат») Пирсона, Колмогорова, Смирнова, Романовского и др.
Критерий Пирсона c 2 - наиболее часто употребляемый критерий согласия. Его достоинство в том, что он может быть использован для проверки гипотезы о любом законе распределения. Рассмотрим применениеc2-критерия для проверки гипотезы о нормальном распределении генеральной совокупности.
- эмпирические частоты, то есть число значений (наблюдений) признака Х, попавших в соответствующий частичный интервал:
Для того чтобы дать обоснованный ответ о случайном или неслучайном расхождении эмпирических и теоретических частот, применим критерий Пирсона (критерий c 2). В качестве меры расхождения между эмпирическими и теоретическими частотами будем рассматривать специально подобранную случайную величину:
,
где 
- эмпирические частоты, найденные по данным выборочного наблюдения;
- теоретические частоты, найденные в предположении справедливости гипотезы Н0.
Итак, чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:
1) по данным выборки объема n найти теоретические частоты 
;
2) найти наблюдаемое значение критерия 
;
3) из таблицы критических точек распределения c 2 по заданному уровню значимости a и числу степеней свободы k=s- 3 найти 
(a, k) - границу правосторонней критической области;
4) сравнить 
с 
(a, k) и сделать вывод.
29. Проверка гипотезы об однородности двух выборок.
Предположим, что имеется две выборки. Проверяется гипотеза H0: выборки однородны, т. е. извлечены из одной и той же генеральной совокупности.
Критерий Колмогорова – Смирнова сравнивает эмпирические функции распределения 
и 
:
.
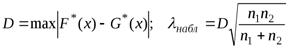Критическое значение l кр определяется из таблицы критических значений Колмогорова – Смирнова по уровню значимости a. Если l набл < l кр, то нет оснований отвергнуть нулевую гипотезу. Критерий Колмогорова сравнивает эмпирическую ф-цию с теоретической.
30. Однофакторный дисперсионный анализ. Уровни фактора. Межгрупповая и внутригрупповая вариации.
xij = m + Fi + eij
где xij – значение исследуемой переменной, полученной на i-м уровне (i=1, 2, …, m) j-го фактора (j=1, 2, …, n)
m - общая средняя
Fi – эффект, обусловленный влиянием i-го уровня фактора
eij – случайная компонента (возмущение), вызванное влиянием неконтролируемых факторов (т.е. вариацией переменной внутри отдельного уровня); обычно считается, что eij имеет нормальный закон распределения N(0; s2)
Уровень фактора. Некоторая его мера или состояние (номер партии, тип технологии, вид обработки и т.п.). Влияние уровней фактора может быть как фиксированным, или систематическим (модель 1), так и случайным (модель 11).
Межгрупповая дисперсия является мерой колеблемости частных (групповых) средних (xi) около общей средней (x) и исчисляется по формуле
δ2 = ∑ (i-)2 × ƒ/ ∑ƒ,
где f – количество единиц совокупности в каждой i -й группе.
Вариацию, обусловленную влиянием прочных факторов, характеризует в каждой группе внутригрупповая дисперсия (σi 2), которую определяют по следующей формуле:
σi2 = ∑ (x - i)2 / n.
Средняя из внутригрупповых, или частных дисперсий определяется по формуле средней арифметической взвешенной дисперсий групп
σi2 = ∑ σi2 × ƒ/ ∑ƒ.
31. Однофакторный дисперсионный анализ. Основные предпосылки.
32. Однофакторный дисперсионный анализ. Виды моделей в зависимости от уровней фактора. Формулировки основной гипотезы.
Однофакторная дисперсионная модель имеет вид:
,
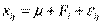Где 
-значение исследуемой переменной, полученной на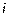 
-м уровне фактора (
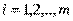) с 
-м порядковым номером (
);
- общая средняя;
- эффект, обусловленный влиянием 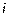-го уровня фактора, т.е. вариация переменной между отдельными уровнями фактора;
-случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельного уровня фактора.
Влияние уровней фактора может быть как фиксированным или систематическим (модель I), так и случайным (модель II).
Пусть, например, необходимо выяснить, имеются ли существенные различия между партиями изделий по некоторому показателю качества, т.е. проверить влияние на качество одного фактора - партии изделий. Если включить в исследование все партии сырья, то влияние уровня такого фактора систематическое (модель I), а полученные выводы применимы только к тем отдельным партиям, которые привлекались при исследовании. Если же включить только отобранную случайно часть партий, то влияние фактора случайное (модель II).
Для модели I с фиксированными уровнями фактора Fi (i=1,2,...,m) – величины неслучайные, поэтому гипотеза H0 примет вид Fi = F* (i = 1,2,...,m), т.е. влияние всех уровней фактора одно и то же. В случае справедливости этой гипотезы.
Для случайной модели II слагаемое Fi в выражении xij = μ + Fj + εij – величина случайная. Обозначая ее дисперсией:
Гипотезы:
H0: Различия между градациями фактора (разными условиями) являются не более выраженными, чем случайные различия внутри каждой группы.
H1: Различия между градациями фактора (разными условиями) являются более выраженными, чем случайные различия внутри каждой группы.
33. Понятие о двухфакторном дисперсионном анализе. Постановка задачи.
Двухфакторная дисперсионная модель имеет вид:
,
где 
-значение наблюдений в ячейке 
с номером 
;
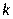общая средняя;
- эффект, обусловленный влиянием 
-го уровня фактора 
;
- эффект, обусловленный влияние 
-го уровня фактора 
;
- эффект, обусловленный взаимодействием двух факторов и 
;
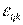- случайная компонента, или возмущение, вызванное влиянием кнеконтролируемых факторов, т.е. вариация переменной внутри отдельных уровней факторов.
Задача двухфакторного дисперсионного анализа заключается в проверке эффекта влияния обоих факторов на зависимую переменную одновременно, а не по отдельности. Кроме этого, в проверке гипотезы об эффекте взаимодействия между двумя независимыми переменными.
Постановка задачи может выглядеть следующим образом:
- проверить нулевую гипотезу об отсутствии эффектов влияния первого фактора на результативный признак;
- проверить нулевую гипотезу об отсутствии влияния второго фактора на результативный признак;
- проверить нулевую гипотезу об отсутствии совместного влияния факторов на результативный признак.
34. Понятие о двухфакторном дисперсионном анализе. Основные предпосылки.
С принципиальной точки зрения многофакторный дисперсионный анализ отличается от однофакторного дисперсионного анализа только количеством рассматриваемых факторов. К основным предпосылкам дисперсионного анализа относятся следующие:
1. Математическое ожидание возмущения ε ij равно нулю для любых i, т. е.
(2)
2. Возмущения ε ij взаимно независимы.
3. Дисперсия переменной (или возмущения) постоянна для любых, т. е.
(3)
4. Переменная хij (или возмущение ε ij) имеет нормальный закон распределения N(0,σ2)
Отклонение от основных предпосылок дисперсионного анализа — нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при неравном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется планировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учитывать при подсчете числа степеней свободы.
35. Понятие о двухфакторном дисперсионном анализе. Расчёт межгрупповых и внутригрупповых вариаций.
Вариация, обусловленная влиянием фактора, положенного в основу группировки, называется межгрупповой вариацией и характеризуется межгрупповой дисперсией (δ2).
Межгрупповая дисперсия является мерой колеблемости частных (групповых) средних (xi) около общей средней (x) и исчисляется по формуле
δ2 = ∑ (i-)2 × ƒ/ ∑ƒ,
где f – количество единиц совокупности