Лабораторная работа №2
Цель работы: экспериментальное и теоретическое исследование цепи с параллельным соединением резистора,катушки индуктивности, конденсатора, изучение резонансных явлений в цепи.
План работы:
1. Определениепараметров заданной цепи.
2. Расчет и получение режима резонанса напряжений.
3. Расчет последовательной цепи символическим методом.
4. Построение векторных диаграмм напряжений и токов.
 |
| задано | замер | расчет | ||||||||||
| С, мкФ | 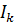 ,
A ,
A
| U, B | P,

| I, A |  ,
A ,
A
| 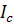 ,
A ,
A
| g,

| 

| 

| 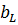 , ,

| 

| C,

|
| 1,7 | 1,2 | 2,2 | 0.0077 | 0,013 | 0,0024 | 0,013 | 0,017 | 54,14 |
2. Расчет параметров заданной цепи
2.1 Активная проводимость резистора,

2.2 Мощность потерь в катушке индуктивности

где, P – измеренная активная мощность всей цепи.
2.3 Из условия

Определить угол сдвига фаз между напряжением и током катушки индуктивности, град:
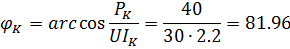
2.4 Полная проводимость катушки индуктивности

2.5 Из условия
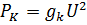
Определить активную проводимость катушки

2.6 Из условия

Определить реактивную проводимость катушки индуктивности

2.7 активная и индуктивная составляющие тока катушки A:

 =
= 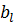 U=1,7
U=1,7
2.8.Емкостная проводимость конденсаторов, Ом
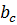 =
= 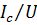 =
=  =0,017
=0,017
2.9. Из условия
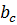 =
= 
определить уточненное значение емкости, мкф:
 =
=  =54,14
=54,14
Где 
2.10. Активная составлявшая тока всей цепи, A:
 =
=  +
+  =1+1,7=2,7
=1+1,7=2,7
2.11. Реакция составлявшая тока всей цепи, A:
 =
=  +
+  =1,77-2,2=-0,5
=1,77-2,2=-0,5
2.12.. Реактивная мощность всей цепи, вар:
Q=U  =130
=130 
 , ,

| 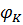 ,
град ,
град
|  ,
А ,
А
|  ,
А ,
А
|  ,
А ,
А
|  ,
А ,
А
| Q, вар | S, ВА |  ,
град ,
град
|
2.13.Полная мощность всей цепи, ВА:
S=UI=130 
2.14.Угол сдвига фаз между напряжением U и точком I.
Град:
 =arc tg
=arc tg 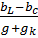 =
=  = -36,87
= -36,87
2.15. Результаты расчетов занести в формы 2.1 и 2.2.
2.16. построить векторную диаграмму на основе уравнения
I=  +
+  +
+ 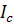
и по данным формы 2.2, взяв ориентирующий вектор произвольно расположенный на плоскости вектор напряжения U. Пример на рис.2.2. Векторные диаграммы строятся с обязательным соблюдением тока и масштаба напряжения.
3.РАСЧЕТ И ЭКСПЕРИМЕНТАЛЬНОЕ ПОЛУЧЕНИЕ РЕЖИМА РЕЗОНАНСА ТОКОВ
3.1.Из условия резонанса в данной цепи
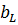 =
=  =
= 
определить расчетное значение резонансной емкости, мкФ:
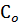 =
=  =
=  =
=  =41,4
=41,4
где 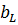 -рассчитанная (форма2.1) индуктивная проводимость катушки.
-рассчитанная (форма2.1) индуктивная проводимость катушки.
3.2. Ток в неразветвленной части цепи при резонансе
 =
= 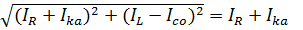 =
=  ,
,
так как
 =1,7
=1,7
3.3.Активная мощность цепи, ровная при резонансе полной мощности, Вт:
 =S=U
=S=U 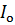 =221=130
=221=130 
 =1,7
=1,7
так как
 =O и cos
=O и cos  =1.
=1.
3.4. Установить на стенде расчетную (или близкую к ней) величину резонансной емкости 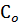 и включить цель. При необходимости (в случае значительного расхождения расчетного тока
и включить цель. При необходимости (в случае значительного расхождения расчетного тока  с установившимся в цепи) проверить на стенде ток в неразветвленной части цепи на минимум, увеличивая или уменьшая емкость конденсаторов относительно расчетной
с установившимся в цепи) проверить на стенде ток в неразветвленной части цепи на минимум, увеличивая или уменьшая емкость конденсаторов относительно расчетной 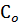 .
.
3.5. Убедиться в справедливости соотношения п. 3.3 по показаниям приборов (ваттметра, вольтметра и амперметра).
3.6. После завершения измерений выключить цепь переключателем III.
Форма 2.3
 ,
мкФ ,
мкФ
|  ,
A ,
A
| 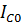 ,
A ,
A
| 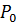 , ,

| |
| Расчет | 41,4 | 1,7 | 1,7 | |
| Эксперимент | 1,4 | 1,6 |
3.7.результати расчетов и измерений занести в форму 2.3.
3.8. Уточнение значение резонансной емкости, мкФ:
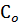 =
= 
Где 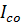 -показания приборов в режиме резонанса.
-показания приборов в режиме резонанса.
3.9. по данным форм 2.2 и 2.3 построить векторную диаграмму для резонанса токов.
4. РАСЧЕТРАЗВЕТВЛЕННОЙ ЦЕПИ СИМВОЛИЧЕСКИМ МЕТОДОМ
4.1.Исходные данные для расчета:
а) ранее рассчитанные проводимость резистора g, активная и реактивная проводимости катушки индуктивности  и
и 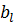 (cv. форму 2.1);
(cv. форму 2.1);
б) новое, заданное преподавателем, ориентировочное значение значение  мкФ.
мкФ.
4.2 Емкостная проводимость, соответствующая новой заданной емкости,  :
:
 =2
=2 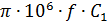 .
.
4.3. Комплексные проводимости ветвей цепи,  :
:
катушки индуктивности
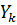 =
=  -
-  =0,0024-j0,013
=0,0024-j0,013
резистора
 =g=0,0077, (
=g=0,0077, (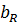 =0);
=0);
конденсатора
 =
=  , (
, ( =0),
=0),
где j=  - мнимая единица.
- мнимая единица.
4.4. Комплексная проводимость всей цепи.  :
:
 +
+  =(g+
=(g+  )+j(-
)+j(- 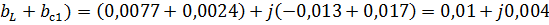
4.5.Ток в неразветвленной части цепи, А:
I=YU= 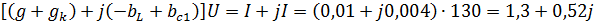
где U=U – комплекс напряжения цепи, записанный в виде действительной части, В.
Например,
,U=130 B;
I, I – действительная и мнимая части комплекса тока, А.
4.6. Комплексы токов в ветвях, А:
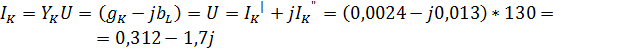


Где  ,
, 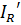 ,
,  -действительные части комплексов токов, А;
-действительные части комплексов токов, А;

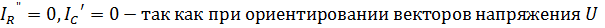
по оси действительных чисел вектор  совпадает по фазе с U, а вектор
совпадает по фазе с U, а вектор  опережает U на угол
опережает U на угол  .
.
4.7 Модули комплексов токов, А:
неразветвленной части цепи

катушки индуктивности

Резистора

конденсаторов

так как в рассматриваемом частном случае
 .
.
4.8 определить активную мощность цепи P как действительную часть комплекса полной мощности всей цепи

где I – сопряжений комплекс тока. Рассчитанного в п. 4.5, то есть
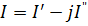
форма 2.4
 мкФ
мкФ
|  , ,
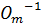
| I, A |  ,
A ,
A
|  ,
A ,
A
|  , ,
| P,

| |
| расчет | 0,017 | 1,7 | 1,001 | 2,21 | |||
| эксперимент | 1,2 | 2,2 | |||||
4.9. Установить на стенде заданную величину емкости конденсаторов и включить цепь.
4.10. результаты расчетов и измерений занести в формулу 2.4. Расчет и экспериментальные данные не должны отличаться более чем  5%.
5%.
После производства измерений цепь выключить.
4.11. Уточненное значение емкости конденсаторов, мкФ:
 ,
,
где  и U – показания приборов для заданной цепи.
и U – показания приборов для заданной цепи.
4.12. По рассчитанным действительным и мнимым частям комплексов токов построить векторную диаграмму. Пример построения на рис. 2.3. Правильно построенная векторная диаграмма должна соответствовать уравнению
I=  ,
,
что показано на рис. 2.3. переносом векторов 