Свободные многочастотные нелинейные колебания бесконечно длинного тонкого прямолинейного стержня впервые изучались в работе [13], на основе уравнений модели Бернулли-Эйлера. В отличие от стандартного подхода к подобным задачам, авторы при формулировке проблемы первично выдвинули предположение о существовании фазового синхронизма между волнами:
(12) 
; 
,
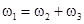где 
и 
- частоты и соответствующие волновые векторы резонансно взаимодействующих волн. Возникал вопрос о том, волны какого типа могут могут вовлекаться в резонансное взаимодействие. Было обнаружено существование двух типов резонансных триад в стержне. Триада одного типа состояла из высокочастотной продольной волны, 
, и пары низкочастотных изгибных волн, 
и 
, в то время как триада другого типа состояла из высокочастотной изгибной волны, , и пары низкочастотных волн, и 
, одна из которых была продольной, а вторая изгибной. Эволюционные уравнения волновых триплетов описываются уравнениями
(13) 
,
где 
- комплексные амплитуды волн;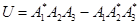 
- кубический потенциал трехволнового взаимодействия. Эти уравнения обладают первыми интегралами в форме соотношений Менли-Роу
(14) 
с помощью которых ограниченные решения эволюционных уравнений (13) всегда выражается через эллиптические функции Якоби. Из соотношений Менли-Роу (14) следует, что полная энергия волн триплета сохраняется. Кроме того, высокочастотная волна 
всегда неустойчива по отношению к малым возмущениям со стороны ее низкочастотных волн 
и 
. Это явление называется распадной неустойчивостью высокочастотной волны.
Этот существенный результат можно просто проиллюстрировать, рассматривая условия фазового синхронизма (12) как законы сохранения в терминах квазичастиц, поскольку всякая пара 
может ассоциироваться, соответственно, с энергией и импульсом кванта, в то время как соответствующие величины 
в выражении (14) можно трактовать как число квантов 
-го типа. Весьма вероятно, что с точки зрения задач динамической неустойчивости механических систем, трехволновые взаимодействия наряду с и другими резонансными взаимодействиями играют ключевую принципиальную роль. Исследование нелинейных колебаний типичных элементов конструкций, таких как стержни, балки, кольца, тонкие пластинки и оболочки, доказывают свойственность таких резонансных взаимодействий для большинства механических систем. В контексте задач динамической неустойчивости заметим, что трехволновые резонансные взаимодействия могут также ассоциироваться с так называемым сценарием взрывной неустойчивости в упругих системах [14]. Математически, взрывная неустойчивость может описываться уравнениями того же типа, что и уравнения (13). Но потенциал взаимодействия должен быть другого вида, например 
. Это означает, что амплитуды волн могут возрасти до бесконечности за конечный промежуток времени, т.е. 
. Физически это означает, что упругая система необходимо должна быть подвержена действию хотя бы малых нагрузок, зависящих специальным образом от амплитуд волн.
Литература
1. Euler L. (1728), Solutio problematis de invenienda curva quam format lamina utcunque elastica in singulis punctis a potentiis quibuscunque sollicitata, Comment Acad. Sci. Petrop., 3, Opera II-10, 70-84.
2. Euler L. (1744), Methodus inveniendi lineas curvas maximi proprietate gaudentes, Lausanne, Geneve, Opera I-24.
3. Лаврентьев М.А., Ишлинский А.Ю. (1949), Динамические формы потери устойчивости в упругих системах, Докл. АН СССР, 64 (6), 779-782.
4. Вольмир А.С. (1972), Нелинейная динамика пластинок и оболочек, М.: Наука.
5. Березовский А.А., Жерновой Ю.В. (1981), Нелинейные продольно-поперечные стационарные волны в упругих стержнях, В сб.: Мат. Физика, Киев, Наукова думка, 30, 41-48.
6. Болотин В.В. (1956), Динамическая устойчивость упругих систем, М.: Гостехиздат.
7. Беляев Н.М. (1924), Устойчивость призматических стержней под действием периодических нагрузок, В сб.: Инженерная и Строительная Механика, Ленинградский ун-т, 25-27.
8. Капица Л.П. (1951), Динамическая устойчивость маятника на вибрирующей точке подвеса, ЖЭTФ, 21 (5), 110-116.
9. Челомей В.Н. (1956), О возможности стабилизации упругих систем с помощью вибраций, Докл. АН СССР, 110 (3), 345-347.
10. Болотин В.В. (1951), О поперечных вибрациях стержней, вызванных периодическими продольными нагрузками, В сб.: Поперечные Колебания и Критические Скорости, 1, 46-77.
11. Kauderer H (1958), Nichtlineare Mechanik, Springer, Berlin.
12. Haken H. (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
13. Ерофеев В.И., Потапов А.И. (1985), Трехчастотные резонансные взаимодействия продольных и изгибных волн в стержне, В сб.: Динамика систем, Горьковский ун-т, 75-84.
14. Новиков В.В. (1988), О неустойчивости упругих оболочек как проявлении внутреннего резонанса, ПММ, 52, 1022-1029.
[1] Кубическая нелинейность в этом уравнении в работе [4] не принималась в расчет.
[2] Нелинейность волнового уравнения также не учитывалась при численных расчетах в работе [4].
[3] В системе возникает резонанс, как только 
, что соответствует целому числу четвертей волн укладывающихся по длине стержня. В этом случае система не допускает стационарного решения в форме стоячих волн, хотя резонансное решение для продольных волн можно легко получить с помощью метода Даламбера.
[4] Вопрос сохранения квазипериодических орбит представляет собой одну из ключевых проблем современной физики, которая находится в постоянном развитии [12].
[5] На практике резонансные свойства системы следует прямо связать с порядком итерации асимптотической процедуры. Например, если рассматривается первое приближение, то резонансы, возникающие во втором порядке по 
в расчет не берутся.