МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«Южный федеральный университет»
Физический факультет
Кафедра нанотехнологии
КУРСОВАЯ РАБОТА
по дисциплине «Методы анализа и контроля наноструктурированных материалов и систем»
на тему: «Спектроскопия рэлеевского рассеяния »
Выполнила:
Студентка Зубарева Владислава Олеговна
Курс 3
Группа №9
Руководитель:
ассистент кафедры нанотехнологии, к.ф.-м.н.
Авраменко Марина Владиславовна
Ростов-на-Дону
2018 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1. РАССЕЯНИЕ СВЕТА.. 4
1.1 Природа явления. 4
1.2 Рассеяние света: виды.. 5
2. ПРИМЕНЕНИЕ МЕТОДА В ИССЛЕДОВАНИИ ОДНОСТЕННЫХ НАНОТРУБОК.. 14
2.1 Экспериментальная методика. 14
2.2 Применениеметода. 17
2.2.1 Электронные переходы нанотрубок с независимо определенной структурой. 18
2.2.2 Зависимость поляризации от электронных переходов в нанотрубке 20
2.2.3 Стабильность структуры нанотрубки в направлении ее оси. 21
2.2.4 Взаимодействие нанотрубок. 21
ЗАКЛЮЧЕНИЕ. 24
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.. 25
ВВЕДЕНИЕ
Рассеяние света представляет собой излучение вторичных электромагнитных волн электронами, колебания которых были вызваны падающим на рассеивающий материал светом. В данной курсовой работе рассмотрены различные виды рассеяния света, а именно: рассеяние Мандельштама-Бриллюэна и комбинационное рассеяние (процессы неупругого рассеяния); рассеяние Ми, Тиндаля и рэлеевское рассеяние (процессы упругого рассеяния). Особое внимание уделяется рэлеевскому рассеянию на частицах, размеры которых значительно меньше длины возбуждающего света. Для него рассмотрены природа его рассеяния, вывод уравнения Рэлея, явления, причиной которых является данный вид рассеяния. На процессе рэлеевского рассеяния основан современный метод оптического исследования материалов, спектроскопия рэлеевского рассеяния, которая используется для описания различных свойств газов и их смесей, подтверждения теоретических вычислений посредством сравнения больших объемов данных о том или ином объекте, и наконец, для исследования индивидуальных одностенных нанотрубок, поскольку этот метод позволяет получить информацию об электронных переходах в структуре нанотрубки, чему и посвящена вторая глава курсовой работы.
|
|
РАССЕЯНИЕ СВЕТА
Природа явления
С классической точки зрения процесс рассеяния света по своей природе обусловлен световой электромагнитной волной, которая проходит через вещество и вызывает колебания электронов в атомах или молекулах рассеивающего материала. После этого данные электроны становятся источниками вторичных электромагнитных волн, распространяющихся во всех направлениях (стоит учитывать, что некоторые волны могут быть когерентны между собой и интерферировать) [1].
Материал рассеивающего вещества играет большую роль в рассеянии света. Это обусловлено тем, что в однородной среде вторичные волны полностью гасят друг друга по всем направлениям за вычетом направления распространения падающей (первичной) волны. Таким образом, в однородной среде рассеяние света не происходит.
По-другому обстоят дела в случае неоднородных сред, здесь рассеяние света возникает. Дифрагируя на неоднородностях среды, световые волны дают дифракционную картину, обладающую достаточно равномерным распределением интенсивности во всех направлениях [1]. Сделаем вывод: рассеяние света – есть дифракция на мелких неоднородностях среды.
|
|
Среды, в которых происходит рассеяние света, называются мутными средами. Дымы, туманы, взвеси и суспензии в жидкостях, эмульсии и твердые тела могут быть примерами сред, в составе которых есть мелкие частицы с показателем преломления, отличным от показателя преломления окружающей среды [2].
В оптической спектроскопии не следует пренебрегать эффектом рассеяния и в положительном, и в негативном аспектах. С одной стороны, оно представляет собой причину целого ряда некорректных фотометрических измерений, а с другой – дает доступ к новому полю исследований и возможности произвести измерения, раннее неосуществимые другими методами [3].
В связи с разнообразием и обилием факторов, определяющих рассеяние света, большую сложность составляет дальнейшее развитие одновременно единого и детального способа его описания для различных случаев. Поэтому рассматривают отдельные ситуации в зависимости от рассеивающего материала и процесса возникновения явления.
Рассеяние света: виды
Сам термин «рассеяние» предполагает различные физические явления: отражение, преломление, дифракцию и другие процессы, влияющие на геометрию траектории луча света, а также изменяющие его длину волны. В связи с последним рассеяние бывает двух типов. Процесс рассеяния света может быть упругим (то есть происходить без обмена энергией между светом и веществом) и неупругим (то есть между светом и веществом может происходить перераспределение энергии).
|
|
Неупругое рассеяние
Если частота (длина вторичной волны) изменяется при рассеянии, то такое рассеяние называется неупругим. В неупругом рассеянии выделяют рассеяние на оптических и акустических фононах: это комбинационное (рамановское) рассеяние и вынужденное рассеяние Мандельштама-Бриллюэна. Такие виды рассеяния встречаются в конденсированных средах.
Мандельштама-Бриллюэна рассеяние (МБР) – рассеяние света на тепловых звуковых волнах или же на адиабатических флуктуациях плотности конденсированных сред, сопровождающееся изменением частоты. Данные флуктуации могут быть вызваны беспорядочным движением молекул вещества и их можно представить в виде результата интерференции упругих случайных волн различных частот, которые распространяются в среде по всевозможным направлениям. Максимум интенсивности света, рассеянного таким образом на упругой волне с длиной волны Λ, наблюдается в направлении ϴ, отвечающем условию Брэгга-Вульфа:
2n Λsin ϴ/2 = λ,
где n – показатель преломления, λ – длина волны света в вакууме [4].
В различных средах наблюдается разное количество компонент Мандельштама-Бриллюэна. Так, в жидкостях можно встретить 2 компоненты Мандельштама-Бриллюэна, в твердом аморфном теле – 4 компоненты, обусловленных поперечными и продольными гиперзвуковыми волнами при ϴ, не равном нулю [5]. Наибольший интерес и практическое применение представляют целых 24 компоненты Мандельштама-Бриллюэна в кристаллах в следствие анизотропии скоростей распространения гиперзвука и возбуждающего и рассеянного света, это свидетельствует о широкой применимости данного рассеяния в анализе акустических свойств твердых тел.
Комбинационное рассеяние света (КРС), (в иностранной литературе – эффект Рамана) – рассеяние света в газах, жидкостях и кристаллах, сопровождающееся заметным изменением его частоты. Число и расположение появляющихся в спектре линий рассеянного излучения определяется молекулярным строением вещества [6]. Чем больше в молекуле атомов, тем разнообразнее ряд ее внутренних движений и соответственно богаче спектр рассеянного ею света.
В процессе КРС вещество и свет обмениваются энергией. В результате взаимодействия с налетающим и испущенным фотонами света изменение частоты первичного излучения (уменьшение в случае стоксового рассеяния и увеличение в случае антистоксового рассеяния) всегда сопровождается переходом молекул на другие колебательные или вращательные уровни. Изменение электронной конфигурации молекулы приводит к реорганизации ее ядер, вследствие чего возникают собственные колебания с частотами, типичными для данной молекулы. В результате излучение волн содержит колебательные частоты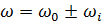 
, где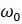 
– это первичная частота, а 
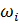– частота собственных колебаний молекул.
Так как в процессе комбинационного рассеяния каждая молекула колеблется независимо от остальных, то данное рассеяние света некогерентно. В связи с этим интенсивность стоксовых и антистоксовых линий пропорциональна числу рассеивающих молекул в единице объема вещества
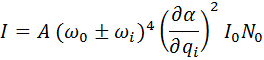
где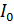 
– интенсивность падающего света, 
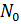– число молекул в единице объема вещества, 
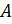– константа, 
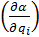– производная поляризуемости по колебательной координате [7].
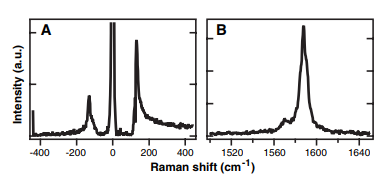
Рисунок 1. Рамановские спектры для одностенной углеродной нанотрубки, рассмотренной при фотонной энергии 1,96 эВ. (А) – стоксова и антистоксова компоненты радиально дыхательного мода. Частота данного мода подразумевает диаметр 1,89 нм. (В) – рамановский спектр G-мода.
Эффект комбинационного рассеяния является фундаментом для широко используемого в сфере изучения нанообъектов метода рамановской спектроскопии. Рамановские измерения предоставляют структурную информацию об одностенных углеродных нанотрубках посредством чувствительности вибрационных модов диаметра и хиральности нанотрубки. Были собраны стоксова и антистоксова компоненты Рамановского спектра радиально дыхательного мода и стоксова компонента связи углерод-углерод (рисунок 1) [8]. Понятие одностенных углеродных нанотрубок будет раскрыто немного позднее, когда пойдет речь об эффекте рэлеевского рассеяния.
Упругое рассеяние света
Если частота (длина волны) света не изменяется при рассеянии, то такое рассеяние называется упругим.
Виды упругого рассеяния света:
1) Рассеяние Тиндаля
2) Рассеяние Ми
3) Рэлеевское рассеяние
Рассмотрим более подробно каждое из них.
Рассеяние Тиндаля – эффект, причиной которого является дифракция света на отдельных взвешенных частицах или элементах структурной неоднородности среды, размеры которых превышают размеры атомов в десятки раз и много меньше длины волны рассеиваемого света. Эффект Тиндаля очень часто путают с понятием опалесценции. Но обычно первый термин связывают с интенсивным рассеянием света в ограниченном пространстве по направлению падающего луча, а второй – со слабым рассеянием света полным объемом рассматриваемого объекта. Наглядно Тиндаля эффект можно наблюдать, например, на кювете с водой, на которую падает белый свет, в ней же размешана одна капля молока. При перпендикулярном к лучу света наблюдении мы обнаружим голубоватое свечение воды, в то время как прошедший через кювету свет будет якобы иметь красноватый оттенок.
Рассеяние Ми – упругое рассеяние на оптических неоднородностях. Размеры этих неоднородностей сравнимы с длиной волны видимого света (λ ~ 0,5 мкм). Такое рассеяние можно понимать как дифракцию плоской волны на идентичных однородных сферах, хаотически рассредоточенных в однородной среде и находящихся друг от друга на расстояниях, сравнительно превосходящих величину длины волны.
Рэлеевское рассеяние. Вывод уравнения Рэлея
Особый интерес в данной работе представляет рэлеевское рассеяние. Прежде чем вдаваться в подробности данного процесса, ознакомимся с выводом важнейшего для процессов рассеяния уравнения.
В классической теории рассеяния вектор электрического поля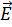 
линейно поляризованной электромагнитной световой волны является причиной усиленного синусоидального колебания «электронного облака» рассеивателя. Степень и легкость происходящих изменений формы «облака» зависит от поляризуемости α. В связи с перемещениями электронов появляется электрический дипольный момент μ. При отсутствии интерференции и поглощения диполь выступает в роли излучающей антенны. Электрическая составляющая 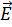входящей световой волны описывается следующим уравнением:
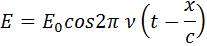
а ортогональная ей магнитная составляющая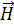 
входящей волны отображается в уравнении:
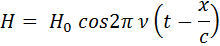
Для дальнейших выводов имеет важность только изменение электрического поля E в рассеивающем центре (x = 0):
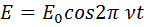
Здесь электрическое рассеянное поле индуцирует, согласно этому, осциллирующий диполь:
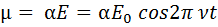
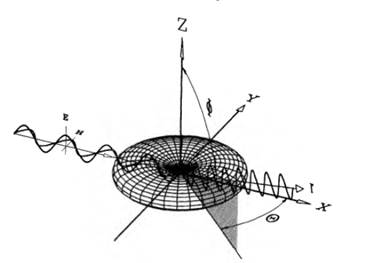
Рисунок 2. Если возбуждающий свет вертикально поляризован и монохроматичен, то распределение рэлеевского рассеяния не завизит от азимутального угла ϴ. Указаны электрическая (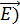
и магнитная (
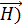составляющие электромагнитного поля.
В изотропных молекулах данные колебания можно наблюдать в ортогональном вышеупомянутым составляющим направлении z -оси. В выводе уравнения интерес представляют мало рассеивающие частицы с размерами, значительно меньшими падающей длины волны. Согласно теории Максвелла, напряженность электрического поля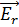 
рассеянного света на расстоянии r (см. рис. 2) и под углом Ф к электрическому диполю 
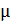, имеет вид:
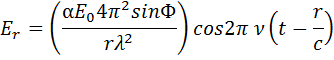
В соответствии с законами физики, интенсивность излучения пропорциональна квадрату амплитуды, в данном уравнении содержимое первых скобок как раз описывает амплитуду рассеянного света. Интенсивность рассеяния также обусловливается интенсивностью падающего света 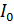, таким образом мы можем получить окончательный вид уравнения Рэлея для интенсивности одноименного рассеяния:
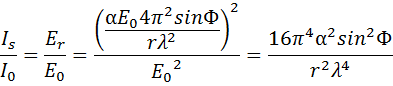
Рэлеевское рассеяние – когерентное рассеяние света (в отличие от противопоставленного ему эффекта Рамана) на оптических неоднородностях, размерные параметры которых значительно меньше длины волны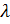 
падающего, возбуждающего света.
В наибольшей степени часто приводимый и наглядный пример рэлеевского рассеяния – голубой цвет неба, отличающийся особенной яркостью в зените Солнца. Рэлеевская теория рассеяния действует применительно к коэффициенту рассеяния
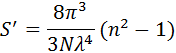
где N – количество молекул в см³, а n – показатель преломления. Здесь, как и интенсивность рассеяния, коэффициент рассеяния увеличивается с уменьшением длины волны возбуждающего света. В связи с этим яркие утренние и вечерние зори мы можем объяснить тем, что солнечный свет пересекает очень толстый слой газа, через который проходит в основном красный свет. Вместе с тем наименьшей длине волны видимого диапазона соответствует фиолетовый цвет, а не голубой. Но мы наблюдаем голубое небо, а не фиолетовое. Причиной этому является спектральная восприимчивость глаза человека и физическая стимуляция [3].
Эффекты рамановского и рэлеевского рассеяния являются фундаментом для очень популярных на сегодняшний день методов оптического изучения различных нанообъектов. Как мы уже увидели в пункте, упоминающем комбинационное рассеяние, в его спектрах встречаются 3 компоненты: две взаимно симметричные стоксовы и антистоксовы компоненты и рэлеевская компонента, которая по факту обрезается в самом методе спектроскопии комбинационного рассеяния. Но считать, что рэлеевская компонента – это лишь то, что мешает нам отчетливо увидеть пики в комбинационном рассеянии, будет ошибочно.
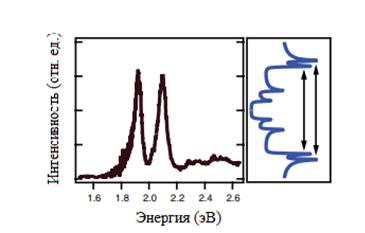
Рисунок 3. Спектр рэлеевского рассеяния на изолированной одностенной углеродной нанотрубке, демонстрирующий переходы E₄₄ и E₃₃ в полупроводниковой нанотрубке.
Рэлеевские спектры предоставляют информацию, которая может сопровождать другие оптические измерения. Рэлеевские данные в отдельных случаях используются в рамановском рассеянии, которое рассматривает электронные резонансы в измерениях отдельных одностенных углеродных нанотрубок. Изображенные на рисунке 2 пики в рамановских спектрах были также рассмотрены посредством рэлеевской спектроскопии (рисунок 3). Рэлеевский спектр был получен первым и показал наличие резонансных значений на 1,92 и 2,10 эВ; в дальнейшем стало возможным выбрать нужное значение возбуждающей энергии рамановского лазера (1,96 эВ), чтобы найти один из рассмотренных переходов. Без таких предварительных знаний о резонансной энергии, нам пришлось бы проводить эксперименты, основанные на трудном и длительном методе проб и ошибок с перебором всех доступных длин волн возбуждающего лазера [8].
Также известно применение спектроскопии рэлеевского рассеяния для изучения различных свойств газов и определения полей потоков [9]. Движение молекул в газе приводит к флуктуациям плотности, по причине которых как раз возникает рэлеевское рассеяние. Рэлеевское рассеяние лазерного излучения является важным способом исследования, его развитие было обусловлено двумя факторами. Первый – это использование интенсивности рэлеевского рассеяния для изучения поля потоков газа и структуры пламени наряду с плотностью и, в некоторых случаях, с составом смеси. Если известно давление, то измерения плотности могут быть преобразованы в температуру в условиях известной смеси идеальных газов. Второй фактор – это использование спектра рэлеевского рассеяния для понимания характеристик атмосферы и сложных (составных) потоков. В большинстве случаев это подразумевает под собой рэлеевское рассеяние в воздухе или в воздухе, содержащим взвесь частиц, и приводит к измерению поля скоростей. В случае молекулярного рассеяния, рэлеевское рассеяние может служить инструментом для описания полей температур и плотностей.
Таким образом, использование данных, полученных с помощью эффекта рэлеевского рассеяния, достаточно обширно. В данной работе появляется термин «одностенные нанотрубки». Именно с исследованием данных нанотрубок чаще всего связывают оптические измерения, основанные на эффекте рэлеевского рассеяния. Во второй части работы рассматриваются различные аспекты таких измерений.