Министерство образования Иркутской области
Государственное бюджетное профессиональное
образовательное учреждение
Иркутской области
«Иркутский авиационный техникум»
(ГБПОУИО «ИАТ»)
С-17-1
«Преобразование графиков функции»
Председатель ЦК: ______________________________________ ()
(подпись, дата)
Руководитель: ______________________________________ (И.С. Сыровая)
(подпись, дата)
Тьютор: ______________________________________ (Е.П. Зайкова)
(подпись, дата)
Обучающийся: ______________________________________ (Е.А. Карышев)
(подпись, дата)
Иркутск 2017
Содержание
Ведение. 3
Три вида геометрических преобразований графика функции. 4
Сжатие и растяжение. 5
Сжатие и растяжение вдоль оси OX.. 6
Сжатие и растяжение вдоль оси OY.. 7
Преобразование симметрии. 8
Преобразование симметрии относительно оси OX.. 9
Преобразование симметрии относительно оси OY.. 10
Параллельный перенос. 11
Параллельный перенос вдоль оси OX.. 12
Параллельный перенос вдоль оси OY.. 13
Пример: 13
Источники. 14
Ведение
Тема: Преобразование графиков функции
Цель: Научиться преобразовывать графики функций
Задачи:
1. Анализ информационных источников по данной теме.
2. Научиться приемам построения графиков.
3. Показать их применение при построении.
4. Анализ полученных данных, вывод.
Три вида геометрических преобразований графика функции
Первый вид - масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
Второй вид - симметричное (зеркальное) отображение относительно координатных осей.
Третий вид - параллельный перенос (сдвиг) вдоль осей OX и OY.
Сжатие и растяжение
На необходимость масштабирования указывают коэффициенты формула и формула отличные от единицы, если формула, то происходит сжатие графика относительно OY и растяжение относительно OX, если формула, то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.
|
|
Применение в науке:
Сжатие и растяжение вдоль оси OX
a>1 График функции y=f(ax) получается сжатием графика функции y=f(x) вдоль оси x в a раз.

Пример:График функции y=f(ax),  получается сжатием графика y=f(x) вдоль оси Ох к оси Оу в 3 раза при или растяжением вдоль оси Ох к оси Оу в
получается сжатием графика y=f(x) вдоль оси Ох к оси Оу в 3 раза при или растяжением вдоль оси Ох к оси Оу в  раз. Получаем
раз. Получаем  и
и 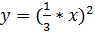

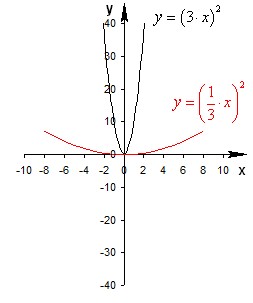
Сжатие и растяжение вдоль оси OY
k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси OY в k раз.

Пример: График функции y=af(x),  получается растяжением графика
получается растяжением графика  вдоль оси Оу от оси Ох в 3раз или сжатием вдоль оси Оу к оси Ох в
вдоль оси Оу от оси Ох в 3раз или сжатием вдоль оси Оу к оси Ох в  раз.Получаем
раз.Получаем  и
и 


Преобразование симметрии
На необходимость этого преобразования указывают знаки «минус» перед коэффициентами формула(в этом случае симметрично отображаем график относительно оси OX) и формула (в этом случае симметрично отображаем график относительно оси OY). Если знаков «минус» нет, то этот шаг пропускается.
Преобразование симметрии относительно оси OX
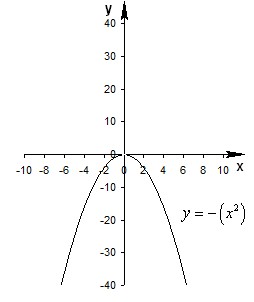
График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика с осью x остаются неизменным. 
График функции y=f(-x) получается симметричным отображением графика  относительно оси Оу. Получаем
относительно оси Оу. Получаем 


Преобразование симметрии относительно оси OY
График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.
|
|
Замечание. Точка пересечения графика с осью y остается неизменно. 
График функции y=-f(x) получается симметричным отображением графика
 относительно оси Ох. Получаем
относительно оси Ох. Получаем 

Параллельный перенос
Это преобразование производится В ПОСЛЕДНЮЮ ОЧЕРЕДЬ при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а – вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b – вниз на |b| единиц.
Применение в науке:
Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.
Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.