Алгоритм нахождения кратчайших маршрутов

ЛАБОРАТОРНАЯ РАБОТА №6

Маршруты и связность в неориентированных графах

 

 

Цель работы: приобретение практических навыков в определении характеристик связности неориентированных графов, изучение различных алгоритмов нахождения кратчайших маршрутов.

Теоретическая справка

Виды маршрутов в неориентированных графах

 

Маршрут М=(v_0,e_1,v_1,e_2,…,e_n,v_n) неориентированного графа G=(V,E) –чередующаяся конечная последовательность вершин и рёбер, начинающаяся и заканчивающаяся вершиной, каждое ребро соединяет две вершины – предыдущую и последующую.

Концевые вершины маршрута – v₀ и v_n, внутренние – все остальные вершины.

Замкнутый маршрут М = (v_0,...,v_n) – концевые вершины совпадают (v₀=v_n), иначе– открытый (v₀ ¹v_n).

Цепь – маршрут, все ребра которого различны.

Простая цепь – маршрут, все вершины которого, а следовательно и ребра, различны.

Цикл – замкнутая цепь, простой цикл – замкнутая простая цепь(маршрут, в котором ребра и вершины различны).

Обозначение: C_n – простой цикл, n ³ 3, n – количество вершин.

P_n – простая цепь, n – количество вершин.

 

C₃ P₅

 

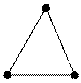
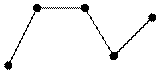
Например:

Дан граф G. Привести примеры маршрута, цепи, простой цепи, замкнутого маршрута, цикла и простого цикла.

 

 

 

 

Маршрут M₁=(1,3,4,5,3,4,6,7,2).

Маршрут M₂=(1,3,4,5,3,4,6,7,1).

Маршрут M₃=(1,5,3,7,1,2).

Маршрут M₄=(1,7,3,4,6,7,1).

Маршрут M₅=(1,5,3,4,6,7,2).

Маршрут M₆=(1,3,4,6,7,2,1).

Для маршрута M₁ вершины 1 и 2 – концевые; 3,4,5,6,7 – внутренние.

Маршрут M₁ – открытый, не цепь и не простая цепь (ребро (3,4) повторяется).

 

Маршрут M₂ – замкнутый, не цикл и не простой цикл (ребро (3,4) повторяется).

 

Маршрут M₃ – не простая цепь (вершина 1 повторяется).

 

Маршрут M₄ – не простой цикл (вершина 7 повторяется).

 

Маршрут M₅ – простаяцепь.

Маршрут M₆ – простой цикл.

 

Связность

Связный неориентированный граф G – любая пара вершин соединена маршрутом (простой цепью) в G.

Компонента связности или компонента графа G – максимальный связный подграф графа G.

 

Любой несвязный граф содержит по крайней мере две компоненты связности.

 

	Любой граф G является объединением своих компонент связности.

.

 

 

	Либо граф, либо его дополнение связны.

À

 

 

Число вершинной связности χ(G) – наименьшее число вершин, удаление которых приводит к несвязному или одновершинному графу.

 

Число реберной связности l(G) – наименьшее число рёбер, удаление которых приводит к несвязному или одновершинному графу.

 

Точка сочленения (разделяющая вершина) – вершина v графа G, удаление которой увеличивает количество компонент связности графа G.

 

Мост – ребро, удаление которого приводит к увеличению числа компонент связности.

Неразделимый граф – граф без точек сочленения.

Блок – максимальный неразделимый подграф графа G.

 

 

 

Например:

 

Граф G: Граф R:

 

 

 

 

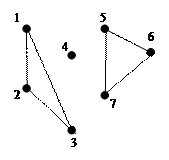
Граф G – связен.

Граф R – несвязен, в графе R три компоненты связности, R₁ = {1,2,3}, R2 ={4}, R3={5,6,7}.

 

 

Граф G1:

 

Граф G1: точки сочленения – вершины a, b, c;

мост – ребро ab.

Граф G1 не является неразделимым;

блоки графа G1: {c,d,e},{c,b,f},{a,g,h,i},{a,b}.

 

 

 

Граф G2:

 

 

Вершинная связность графа G2 равна χ(G2) =1 (удаление вершины 5 приводит к нарушению связности графа G2).

Реберная связность графа G2 равна l(G2)=2 (удаление рёбер (5,7), (5,8) приводит к нарушению связности графа G2).

 

Метрика в неорграфах

Длина маршрута – количество ребер, входящих в данный маршрут, каждое ребро учитывается столько раз, сколько раз оно входит в маршрут.

 

Пусть в графе G маршрут М=(1,3,4,5,3,1,7), тогда его длина равна шести.

 

Обхват графа G – длина минимального простого цикла графа G (если он существует).

Окружение графа G – длина наибольшего простого цикла графа G (если он существует).

Расстояние d(u,v) между двумя несовпадающими вершинами u и v – длина кратчайшей простой цепи, соединяющей эти вершины.

Геодезическая s(u,v) – кратчайшая простая цепь между вершинами u и v,

доставляющая расстояние между этими вершинами.

Матрица расстояний

Матрица расстояний D(G) – квадратная матрица p*p, где p – количество вершин графа G.

D(G)=||d_ij|| i,j=1..p

0, если i=j;

d_ij = d(i,j), если i¹j, существует маршрут (i,j);

¥, если i¹j, не существует маршрут (i,j).

 

Эксцентриситет e(v) вершины v графа G – длина максимальной геодезической, исходящей из вершины v:

e(v)= MAX d(v,u).

uÎV

Диаметр D(G) графа G – максимальный среди всех эксцентриситетов вершин графа G:

D(G)= MAX e(v).

vÎV

Радиус R(G) графа G – минимальный среди всех эксцентриситетов вершин графа G:

R(G)= MIN e(v).

vÎV

Периферия графа G – множество вершин графа G, у которых эксцентриситет равен диаметру.

Центр графа G – множество всех вершин графа G, у которых эксцентриситетравен радиусу.

Например:

Граф G: вес каждого ребра равен 1.

 

Матрица расстояний D_G

 

vj vi								e(vi)
1
2
3
4
5
6

 

Диаметр G: D(G) =3.

Радиус G: R(G) =2.

Периферия графа G = {3,4}.

Центр графа G = {1,2,5,6,7}.

 

Обхват графа G = 3.

Окружение графа G = 7, максимальный простой цикл графа содержит все вершины графа G: ( 1,4,2,7,3,5,6,1 ).

 

 

Алгоритм нахождения кратчайших маршрутов

 

Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной вершины (s)до заданной конечной вершины (t), при условии,что такой путь существует.

Задачи данного типа имеют следующие модификации:

- для заданной начальной вершины s найти кратчайшие пути от s ко всем другим вершинам графа;

- найти кратчайшие пути между всеми парами вершин.

 

Для решения этих задач рассмотрим граф G=(X,Г), дуги которого имеют определенные веса (стоимости). Эти веся задаются матрицей C=[c_ij].

Элементы с_ij матрицы весов C_G могут быть положительными, отрицательными или нулями. Поэтому существует ограничение: в G не должно быть циклов с суммарным отрицательным весом (в этом случае кратчайшего пути не существует). Отсюда также следует, что рёбра (неориентированные дуги) графа G не могут иметь отрицательные веса.

 

Описание ориентированного графа G состоит в задании множества вершин X и соответствия Г,которое показываеткак между собой связаны вершины (т.е. Г(x_i) – множество вершин x_j, для которых в графе существуют дуги (x_i,x_j), x_j достижимы из x_i с использованием путей длины 1). Соответствие Г называется отображением множества X в X, а граф в этом случае обозначается парой G=(X,Г).

Для графа G₁ имеем Г(x1)={x3}

G₁:

 

Будем рассматривать неориентированные ребра, как пары противоположно ориентированных (направленных) дуг с равными весами.

 

 

Алгоритм Дейкстры

 

В общем случае этот метод основан на том, что вершинам приписываются «временные» отметки. Отметки обозначают длины путей от начальной вершины s к данной вершине (причем временные отметки являются верхними границами длин путей). Величины этих пометок постепенно уменьшаются с помощью итерационной процедуры (т.е. процедуры, в которой постоянно повторяется некоторый набор операций). И на каждом шаге итерации одна из временных отметок становится «постоянной» (т.е. окончательно определенной, такой, которая обозначает точную длину кратчайшего пути от s к рассматриваемой вершине.

 

Рассмотрим этот алгоритм для случая, когда вес каждого ребра графа неотрицателен (c_ij ³ 0, ("i,j)).

 

Алгоритм:

Пусть l(x_i) – отметка вершины х_i.

 

Шаг 1. Положить l(s)=0⁺ и примем эту отметку постоянной. Положить l(x_i)=∞ для всех х_i¹s и считать эти отметки предварительными-«временными». Положить p=s.

 

Шаг 2. Для всех х_i Г (р), отметки которых «временные», заменить отметки в соответствии со следующим выражением:

 

l(x_i)← min [l(x_i), l(p)+c(p,x_i)]

 

Шаг 3. Среди всех вершин со временными отметками найти такую, для которой

l(x_i­­­­^*)= min [l(x_i)]

 

Шаг 4. Считать отметку вершины х_i^* постоянной и положить р=х_i^*.

 

Шаг 5. Если p=t, то l(p) является длиной кратчайшего пути. Если p¹t, то перейти к шагу 2.

 

 

Как только длины кратчайших путей будут найдены, сами пути можно получить при помощи рекурсивной процедуры с использованием соотношения, т.к. вершина x_i’ непосредственно предшествует вершине x_i в кратчайшем пути от s к x_i, то для любой вершины x_i соответствующую вершину x_i’ можно найти как одну из оставшихся вершин:

 

l(x_i’)+c(x_i’,x_i)=l(x_i)

Например:

Граф G:

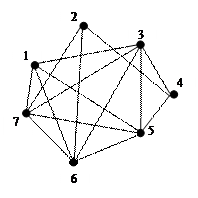Таблица 1. Матрица весов дуг - C(x_i,x _j) для графа G,

 

 

Допустим, что требуется найти все кратчайшие пути от вершины х1 ко всем остальным вершинам.

 

Постоянные отметки будем отмечать знаком ⁺, остальные отметки рассматриваются пока - как «временные».

s – вершина начала пути. Для нашего примера s=x1.

l(x_i) – пометка вершины х_i (равная длине пути от вершины s до x_i).

p – переменная, которая хранит имя вершины с постоянной отметкой.

t – конечная вершина кратчайшего пути от х1.

Г(р) – множество вершин, инцидентных x1 (т.е. вершин x_j, для которых существуют дуги (x_i, x_j)).

C=[c_ij] – матрица весов.

 

Шаг1. p=х1 р – рабочая переменная, которая задает номер/имя вершины начала искомого пути минимальной длины. В данном примере выбрана первой в составе кратчайшего маршрута вершина х1.

Зададим первое приближение длины пути от х1 до всех остальных вершин графа.

l(х1)=0⁺ Отмечаем знаком 0⁺ нулевую отметку - l(х1 ) начала минимального пути из х1 в х1, его длина всегда равна нулю.

l(х2)=l(х3)=...=l(х7)=∞ Устанавливаем знаком ∞ отметки о неизвестной пока длине пути из х1 в вершины (х2 - х7)

 

Делаем Первую итерацию (уточнение расстояния каждой x_j от вершины указанной в р. На этом этапе расчета р=х1.

 

Шаг2.

Г(р)=Г(х1)={х3, х5, х6, х7} – строим вектор вершин смежных вершине указанной в р. Пока р=х1.

Обновим «временные» отметки для всех вершин вектора Г(х1) по формуле: l(x_i)← min [l(x_i), l(p)+c(p,x_i)].

Здесь l(x_i):= min [l(x_i), l(p)+c(p,x_i)] для всех вершин.

l(3)=min(∞,0+4)=4

l(5)= min(∞,0+15)=15

l(6)= min(∞,0+13)=13

l(7)= min(∞,0+1)=1

min(∞,∞,4,15,13,1)=1, это вершина х7.

 

	Отметка вершины х7 становится постоянной, со значением - l(7)=1+, поэтому задаем p=7 и начинаем новую итерацию

 

 

3) l(2)=min(∞, 1⁺+7)=8

l(3)= min(4, 1⁺+2)=3

l(4)= min(∞, 1⁺+∞)=∞

l(5)= min(15, 1⁺+11)=12

l(6)= min(13, 1⁺+12)=12

min(∞,3,8,9,13)=3

l(3)=3⁺

p=3

 

5)l(2)= min(8, 3⁺+∞)=8

l(4)= min(∞, 3⁺+9)=12

l(5)= min(12, 3⁺+12)=12

l(6)= min(13, 3⁺+13)=12

l(2)=8⁺

p=2

 

 

6) l(4)= min(12, 8⁺+4)=12

l(5)= min(12, 8⁺+∞)=12

l(6)= min(13, 8⁺+5)=13

l(4)=l(5)=12⁺

p=4, 5

 

7) l(6)= min(13,12⁺+∞)=13

l(6)=13⁺

p=6

Расчет закончен.

 

Таким образом кратчайшие маршруты от вершины 1:

 

1-2=(1,7,2)=8;

1-3=(1,7,3)=3;

1-4=(1,7,3,4)=(1,7,2,4)=12;

1-5=(1,7,5)=12;

1-6=(1,6)=(1,7,6)=(1,7,2,6)=13;

1-7=(1,7)=1;