ГЛАВА 8 ПРИМЕРЫРЕШЕНИЙ КОНТРОЛЬНЫХ ЗАДАЧ
Проводниковые материалы
8.1.1. Необходимые теоретические сведения и расчетные формулы
Характерная особенность проводников ‑ сильно выраженная электропроводность – обусловлена высокой концентрацией свободных носителей заряда. Их основные параметры: удельные электропроводность σ (См/м) и сопротивление ρ (Ом·м), температурный коэффициент сопротивления αρ (К-1), скорость дрейфа Vд (м/с), подвижность µ (м2/(В·с), длина свободного пробега λ (м) носителей заряда. Они связаны следующими соотношениями:
(8.1)
(8.2)
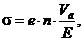(8.3)
где e – заряд электрона; n – концентрация носителей тока; Е – напряженность электрического поля.
Закон Ома в дифференциальной форме для плотности тока в проводнике
(8.4)
Энергия, выделяемая в проводнике при протекании по нему тока,
(8.5)
Из классической теории проводимости электронного газа
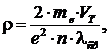(8.6)
где VT – тепловая скорость; λср – средняя длина свободного пробега; me – масса носителей тока.
Квантово-механическая теория электропроводности металлов дает
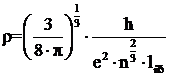(8.7)
Сопротивление протеканию электрического тока связано с рассеиванием носителей заряда на тепловых колебаниях атомов, дефектах структуры, примесях. При температурах, близких к 0 К, тепловые колебания практически отсутствуют, поэтому рассеивание электронов происходит только на структурных дефектах и примесях и удельное сопротивление металла можно представить в соответствии с правилом Маттисона в виде
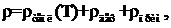(8.8)
где ρтепл(Т) – зависящее от температуры ρ бездефектного металла; rдеф и ρприм – вклад в ρ, обусловленный дефектами и примесями (ρост).
Ряд металлов и сплавов при температуре ниже критической переходят в сверхпроводящее состояние. При этом их сопротивление скачком уменьшается на 12–18 порядков.
|
|
Для чистых непереходных металлов α r »4·10–4 K–1. Переходные и ферромагнитные материалы имеют повышенное αρ (~10–2 K–1).
Согласно правилу Линде, изменение на 1 ат. % концентрации примеси увеличивает ρост на ∆ρост=b·(∆Z)2, где ∆Z – разность валентностей основного металла и примеси, b – постоянный для данной пары коэффициент.
Глубина проникновения переменного электрического поля в проводник
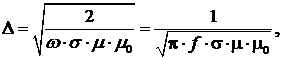(8.9)
где ω и f – соответственно угловая скорость и частота, µ – относительная магнитная проницаемость материала; µ0 – магнитная постоянная
(4π·10–7 Гн·м).
8.1.2. Примеры решения задач
Задача 1
Определить время, в течение которого электрон пройдет расстояние l=1 км по медному проводу, если его ρ= 0,017 мкОм · м, U=220 В. За какое время он прошел бы это расстояние, двигаясь без соударений?
Решение
Из закона Ома получаем
Концентрация электронов (1 электрон на атом) в меди:
где NA ‑ число Авагадро, d ‑ плотность материала, A ‑ атомная (или молярная) масса вещества.
Сравним эту величину с тепловой скоростью носителей.
Так как
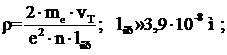
То
Время дрейфа по проводнику:
При отсутствии столкновений электрон двигался бы равноускоренно под действием силы F = e·E, тогда 
и
Задача 2
Требуется изготовить проволоку, которая выдерживает растяжение F =50 H без пластической деформации, причем ее сопротивление должно быть ≤0,02 Ом·м. Определить и сравнить наименьший допустимый диаметр проволоки. Какая экономически более выгодна, если цена алюминия в 1,5 раза ниже цены меди? (Для отожженных Сu и Al: σ т (Си) =70 МПа; σ т(Al)=35 МПа).
|
|
Решение
Наименьший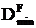 
, при котором отсутствует пластическая деформация,
Наименьший 
, при котором обеспечивается требуемое R при заданной l,
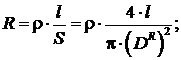
Для меди
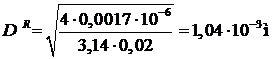
Выбираем 1,04 мм. Для алюминия
Выбираем 1,35 мм.
Выражение для расчета стоимости одного метра проволоки
Тогда
Задача 3
Определить температурный коэффициент линейного расширения 
; и удлинение нихромовой проволоки, если известно, что при повышении температуры от 20 до 1000°С электрическое сопротивление проволоки изменяется от 50 до 56,6 Ом. Длина проволоки в холодном состоянии l =50 м. Температурный коэффициент удельного сопротивления нихрома принять равным 15·10–5 К–1.
Решение
По определению температурный коэффициент сопротивления проволоки:
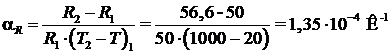
Между температурным коэффициентом сопротивления проводника 
, удельного сопротивления материала 
и линейного расширения существует следующая зависимость:
Тогда
Отсюда удлинение нихромовой проволоки:
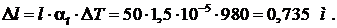
Полупроводниковые материалы
8.2.1. Необходимые теоретические сведения и расчетные формулы
Основными электрофизическими параметрами полупроводниковых материалов являются ширина запрещенной зоны Eg, положение уровня Ферми EF, удельное объемное сопротивление ρV или электропроводность σ, концентрация собственных носителей заряда ni, концентрация донорной примеси Nd, концентрация акцепторной примеси Na, подвижность носителей, время жизни неравновесных или неосновных носителей tn и tp.
|
|
Положение уровня Ферми в собственном полупроводнике определяется выражением
(8.10)
где Ei – уровень, соответствующий середине запрещенной зоны; Nv, Nc – эффективная плотность состояний для дырок валентной зоны и для электронов зоны проводимости соответственно:
(8.11)
(8.12)
где mp*, mn* – эффективные массы дырок и электронов.
Электропроводность собственного полупроводника определяется как
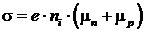(8.13)
В то же время концентрация собственных носителей
(8.14)
Для собственного полупроводника применимо соотношение " действующих масс ":
(8.15)
где n ‑ концентрация электронов, а p ‑ концентрация дырок.
Концентрации носителей в донорных (n>>p) и акцепторных (p>>n) полупроводниках
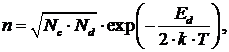(8.16)
(8.17)
Электропроводность примесного полупроводника
(8.18)
Скорость дрейфа носителей в электрическом поле с напряженностью Е определяется выражением
(8.19)
Плотность тока носителей через полупроводник при приложенной напряженности внешнего поля Е будет
(8.20)
Концентрации носителей заряда в полупроводниках связаны с одновременно протекающими процессами генерации и рекомбинации. Скорость рекомбинации определяется в основном концентрацией и временем жизни неосновных или неравновесных носителей заряда, которое определяется по формуле
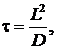(8.21)
где L – диффузионная длина неосновных носителей заряда; D ‑ коэффициент диффузии неосновных носителей, который можно найти из соотношения Эйнштейна:
(8.22)
Убывание концентрации неравновесных носителей заряда в зависимости от времени и расстояния до места возбуждения
(8.23)
(8.24)
8.2.2. Примеры решения задач
Задача 1
Определить, при какой концентрации примесей удельная проводимость германия при температуре 300 К имеет наименьшее значение. Найти отношение собственной удельной проводимости к минимальной при той же температуре.
Данные: собственная концентрация носителей заряда при комнатной температуре ni=2,1·1019 м–3, подвижность электронов μn=0,39 м2/(В·с), подвижность дырок μp=0,19 м2/(В·с)
Решение
Минимум удельной проводимости находим из условия dγ/dn=0. Учитывая, что
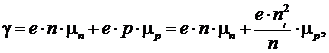
после дифференцирования получим
Решая это уравнение, находим
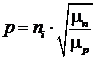
Для германия при 300 К получаем
Таким образом, минимальную удельную проводимость имеет слаболегированный полупроводник р -типа.
Учитывая, что собственная удельная проводимость определяется уравнением gi=e·ni·(μn+μp), находим искомое отношение
Задача 2
В образце кремния n-типа при температуре T=300 К время жизни неосновных носителей заряда τр=5 мкс, их подвижность µp=0,04 м2/(В·с). В одну из плоскостей образца вводится и поддерживается постоянной во времени избыточная концентрация дырок Δp0=1019 м–3. Определить плотность диффузионного тока в непосредственной близости от этой плоскости. На какой глубине концентрация дырок составит 1018 м–3? Считать, что толщина образца значительно больше диффузионной длины носителей заряда.
Решение
Из соотношения Эйнштейна находим коэффициент диффузии дырок
Диффузионная длина неосновных носителей заряда
Распределение дырок по толщине образца при одномерной диффузии характеризуется уравнением Δр=Δр0ехр(–x/Lp), где х – расстояние от поверхности. Плотность диффузионного тока при одномерной диффузии
Для х=0 (т.е. в непосредственной близости от поверхности)
Глубина x1, на которой достигается заданная концентрация неосновных носителей заряда,
