Диэлектрические материалы

8.3.1. Необходимые теоретические сведения и расчетные формулы

Наиболее важными электрофизическими параметрами диэлектрических материалов являются относительная диэлектрическая проницаемость ε, тангенс угла диэлектрических потерь tgd, электрическая прочность E_пр, удельные объемное r_v и поверхностное ρ_s сопротивления. Поляризованность пропорциональна напряженности электрического поля:

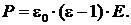(8.25)

Если диэлектрик изотропный, то векторы напряженности электрического поля и поляризованности совпадают по направлению, а электрическое смещение равно

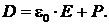(8.26)

Кроме пассивного сопротивления, связанного с наличием свободных носителей заряда, диэлектрики обладают, в отличие от проводников, активным или емкостным сопротивлением, которое зависит от частоты внешнего электрического поля:

(8.27)

где h – толщина диэлектрика; f – частота внешнего электрического поля; ε _o – диэлектрическая проницаемость вакуума; ε – относительная диэлектрическая проницаемость диэлектрика; S – площадь электродов.

Емкость плоского конденсатора

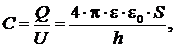(8.28)

где Q – заряд на пластинах; U – разность потенциалов; S – площадь пластин; h – толщина диэлектрика.

Диэлектрическая проницаемость зависит от температуры, поскольку изменяется прочность межатомных связей. В связи с этим вводится температурный коэффициент ε:

(8.29)

В инженерной практике чаще используют понятие температурного коэффициента емкости (ТКЕ) конденсатора на основе данного диэлектрика, поскольку она изменяется пропорционально ε.

Значение диэлектрической проницаемости многокомпонентных диэлектриков определяют по формуле Лихтенеккера, которая, например, для двух составляющих имеет вид

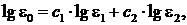(8.30)

где и – относительные диэлектрические проницаемости и объемные концентрации компонентов (с₁+с₂=1).

Для температурного коэффициента диэлектрической проницаемости

(8.31

В переменных электрических полях имеет место рассеяние мощности в диэлектрике из-за необратимых явлений, в том числе вследствие протекания токов смещения. На практике используют величину tgδ, которая входит в выражение для величины потерь в образце диэлектрика

(8.32)

где ω ‑ угловая скорость электрического поля (ω=2·π·f).

При достаточно больших напряженностях поля (больше 10⁶ В/м) в диэлектриках возможен пробой, т.е. утрата изоляционных свойств. Электрическая прочность рассчитывается как

(8.33)

где U_пр – напряжение пробоя диэлектрика толщиной d.

8.3.2. Примеры решения задач

Задача 1

Между пластинами плоского конденсатора без воздушных промежутков зажат лист гетинакса толщиной h =1 мм. На конденсатор подано напряжение U =200 В. Определить поверхностную плотность заряда на пластинах конденсатора σ₁ и на диэлектрике σ_Д. Диэлектрическую проницаемость материала принять равной шести.

Решение

Вследствие поляризации диэлектрика при подключенном источнике постоянного напряжения на пластинах конденсатора удерживается дополнительный заряд σ_Д, так что σ₁=σ_Д+σ₀, где σ₀ – поверхностная плотность заряда на пластинах конденсатора в отсутствие диэлектрика. Тогда

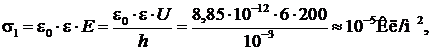
Задача 2

Между плоскими электродами площадью S= 2·10^–4 м² размещены соединенные последовательно две пластины из различных диэлектрических материалов. Одна из них имеет диэлектрическую проницаемость ε₁= 2; удельную проводимость γ₁= 10^–6 См/м; толщину h₁ =1 см. Для другой: ε₂= 3; γ₂= 10^–10 См/м; h₂ =2 см. В момент времени t= 0 к электродам подключено постоянное напряжение U= 5 кВ. Определить напряженность электрического поля в диэлектриках в моменты времени t= 0 и . Найти напряженность электрического поля в диэлектриках при , если к электродам приложено переменное напряжение U =20 В частотой f =50 МГц.

Решение

При постоянном напряжении в момент времени t= 0 напряженность поля в обоих диэлектриках равна 0, так как поляризации еще не произошло.

При распределение постоянного напряжения между пластинами диэлектриков определяется их активными сопротивлениями R₁ и R₂:

где

Отсюда следует, что U₁<<U₂. Так как U=U₁+U₂, то напряженность электрического поля в диэлектриках:

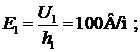
На переменном напряжении при распределение напряжения между диэлектриками определяется модулями полных сопротивлений слоев. Емкостные сопротивления слоев:

Так как x_c1<<R₁ и x_c2<<R₂, то U₁/U₂=x_c1/x_c2. Отсюда Е₁ = 857 В/м; Е₂ =571 В/м.

Магнитные материалы

8.4.1. Необходимые теоретические сведения и расчетные формулы

К статическим магнитным характеристикам материалов относятся:

– напряженность магнитного поля Н (А/м) для линейного и кольцевого проводника с током соответственно

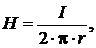(8.33)

(8.34)

где I – постоянный ток в проводнике, А; r – расстояние от проводника до точки, в которой определяется напряженность магнитного поля, м; ω – число витков обмотки; d_ср –средний диаметр кольцевого проводника.

– намагниченность I_м (А/м):

(8.35)

где М – магнитный момент тела; V – объем тела, м³.

Зависимость намагниченности насыщения от температуры:

(8.36)

где α ‑ коэффициент, постоянный для данного материала; Т_к – температура Кюри, К.

– магнитная восприимчивость χ_м, которая характеризует способность вещества изменять свой магнитный момент под действием внешнего магнитного поля

(8.37)

Зависимость магнитной восприимчивости от температуры

(8.38)

где С – постоянная Кюри–Вейса; Т_С – температура Кюри;

– магнитная индукция В (Тл):

(8.39)

где µ₀ – магнитная проницаемость вакуума, µ₀= 4π·10^–7 Гн/м.

– магнитная проницаемость – характеристика среды, в которой возникает магнитное поле. Различают абсолютную µ_а и относительную µ магнитные проницаемости:

(8.40)

(8.41)

Связь магнитной проницаемости с магнитной восприимчивостью

(8.42)

(8.43)

Динамические магнитные характеристики характеризуют поведение ферромагнетиков в переменных магнитных полях:

– потери на гистерезис для каждого материала могут быть определены по площади статической петли гистерезиса. Потери на гистерезис за один цикл в единице объема вещества вычисляют по следующей эмпирической формуле:

(8.44)

где η ‑ коэффициент, зависящий от материала; В_max ‑ максимальная индукция, достигаемая в течение цикла; n ‑ показатель степени 1,6..2,0.

Мощность, расходуемая на гистерезис, может быть представлена в виде

(8.45)

где f – частота тока, Гц; V – объем ферромагнетика.

– потери на вихревые токи

(8.46)

где ξ - коэффициент, зависящий от удельного объемного сопротивления ρ_v и формы магнитного элемента.

– потери на магнитное последействие значительны только при работе ферромагнетиков в импульсном режиме.

Для расчета характеристик магнитных цепей используется закон о полной магнитодвижущей силе F_мд, вытекающий из условия непрерывности магнитного потока:

(8.47)

где Н_i ‑ напряженность магнитного поля на участке силовой линии l_i.

Энергия магнитного поля, создаваемая проводником с током и тороидальной или цилиндрической катушкой соответственно,

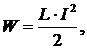(8.48)

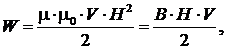(8.49)

где L – индуктивность проводника; V – объем однородного магнитного поля.

8.4.2. Примеры решения задач

Задача 1

В сердечнике трансформатора суммарные удельные магнитные потери на гистерезис и на вихревые токи при частотах 1 и 2 кГц составляют соответственно 2 и 6 Вт/кг (при неизменной максимальной индукции в сердечнике). Рассчитать магнитные потери на вихревые токи в сердечнике на частоте 2 кГц.

Решение

Суммарные потери за 1 цикл перемагничивания линейно зависят от частоты:

Подставляя исходные данные, получим для двух частот:

Вычитая из одного уравнения другое, получаем: Тогда

Задача 2

Диамагнитная восприимчивость меди χ_Cu=–9,5·10^–6. Определить намагниченность и магнитную индукцию в медном проводе при воздействии на него однородного магнитного поля напряженностью Н=100 А/м. Укажите, как ориентированы векторы намагниченности и магнитной индукции друг относительно друга.

Решение

Намагниченность связана с напряженностью магнитного поля соотношением

Магнитная индукция в веществе определяется суммой индукций собственного и внешних полей:

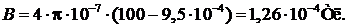
Поскольку медь диамагнетик, векторы В и J антипараллельны.

Задача 3

Магнитная восприимчивость никеля при температурах 400 и 800^оС равна соответственно 1,25·10^–3 и 1,14·10^–4. Определить температуру Кюри и магнитную восприимчивость никеля при температуре Т=600^оС.

Решение

Поскольку, как следует из условия задачи, магнитная восприимчивость падает с увеличением температуры, точка Кюри лежит ниже 400^оС. Известно, что при Т>Т_С, χ_м подчиняется закону Кюри-Вейсса

где С – постоянная, зависящая от природы материала.

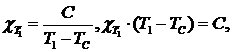
Для нахождения С решим систему уравнени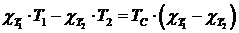й

и

Постоянная Кюри–Вейса

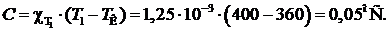
Тогда при Т =600°С
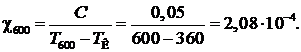