Определим, какие выборочные характеристики лучше всего в смысле несмещенности, состоятельности и эффективности оценивают математическое ожидание и дисперсию.
Пусть из генеральной совокупности (в результате независимых наблюдений над количественным признаком Х) извлечена повторная выборка объема п со значениями признака 
. Выборочная средняя 
, найденная по данным выборки, используется в качестве оценки генеральной средней 
. Покажем, что выборочная средняя является несмещенной оценкой для математического ожидания генеральной средней, т.е. покажем, что математическое ожидание выборочной средней равно генеральной средней.
Пусть из генеральной совокупности последовательно извлечено несколько повторных выборок объема п:
 |
.
Средние значения 
можно рассматривать как независимые, одинаково распределенные случайные величины 
. Так как эти величины имеют одинаковое распределение, то их математические ожидания также одинаковы и равны а, т.е. 
.
Средняя арифметическая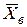 
значений признака 
будет равна
.
Найдем математическое ожидание средней арифметической 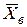. Используя свойства математического ожидания, получим
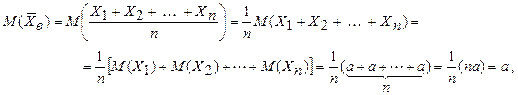
следовательно, 
. Заменив математическое ожидание а на генеральную среднюю 
, получим 
, т.е. средняя выборочная есть несмещенная оценка генеральной средней.
Можно показать, что выборочная средняя является состоятельной и эффективной оценкой генеральной средней, но мы этот вывод опустим.
Без доказательства примем утверждение, что выборочная дисперсия является смещенной оценкой генеральной дисперсии, так как
,
т.е. математическое ожидание выборочной дисперсии не равно генеральной дисперсии.
Несмещенной оценкой дисперсии 
считают «исправленную» выборочную дисперсию
,
т.е. выборочную дисперсию с множителем n/ (n - 1). Проверим это утверждение. Математическое ожидание «исправленной» выборочной дисперсии:
.
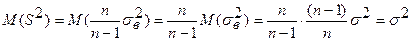Что и требовалось доказать.
Дробь 
называют поправкой Бесселя. При малых значениях п поправка Бесселя довольно значительно отличается от единицы. С увеличением п она быстро стремится к единице и при п > 50 практически нет разницы между выборочной дисперсией и «исправленной» выборочной дисперсией.
«Исправленная» выборочная дисперсия 
является так же и состоятельной оценкой генеральной дисперсии.
Корень квадратный из исправленной выборочной дисперсии 
является оценкой генерального среднего квадратического отклонения.
Из оценки среднего квадратического отклонения можно получить оценку среднего квадратического отклонения выборочной средней 
, которая часто используется для определения средней ошибки для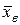 
. Видно, что величина средней ошибки обратно пропорциональна объему выборочной совокупности. Чем больше объем выборки, тем меньше средняя ошибка.
Степень свободы. При рассмотрении понятия дисперсии и среднего квадратического отклонения мы столкнулись с величиной п – 1, которая получила особое название – число степеней свободы. В дальнейшем мы будем обозначать эту величину буквой k. Объясним подробнее его значение.
Рассмотрим некоторый вариационный ряд в котором имеется п вариант. При известном значении средней выборочной этого ряда каждая отдельная варианта жестко связана с остальными п – 1 вариантами. То есть в данном случае имеется п – 1 степеней свободы.