Понижение порядка некоторых типов ДУ высших порядков.
1. 
(ДУ не содержит 
)
Замена 
Получаем для 
ДУ 1-го порядка:
Находим 
. Тогда 
Пример.
Замена 
Получаем для ДУ 1-го порядка:
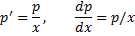
Замечание.
ДУ 
, сводится к ДУ
2. 
(ДУ не содержит явно 
)
Замена 
. Подставим в ДУ:
ДУ 1-го порядка относительно 
. Решая его, получаем общее решение
.
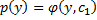с разделяющимися переменными
=dx
Пример.
.
Замена 
. Подставим в ДУ:
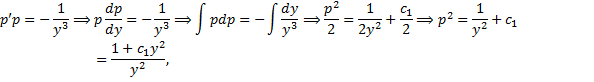
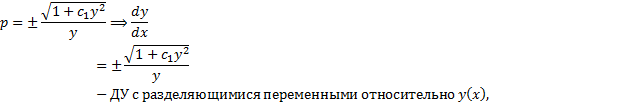
Линейные ДУ (ЛДУ) n-го порядка: однородные (ЛОДУ) и неоднородные (ЛНДУ). Теорема существования и единственности решения. Линейный дифференциальный оператор. Свойства линейного дифференциального оператора и линейность пространства решений ЛОДУ.
ЛДУ n-го порядка (неоднородное):
Коэффициенты 
и правая часть 
– функции, непрерывные на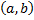 
или на 
. Для 
. Разделим на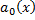 
. Получим ДУ вида
(2.6.1)– ЛНДУ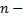 
го порядка. Соответствующее ЛОДУ:
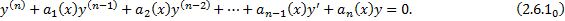
Задача Коши для ДУ: найти частные решения, удовлетворяющие начальным условиям:
где 
.
Теорема существования и единственности решения задачи Коши для ЛДУ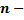 
го порядка
Пусть 
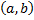непрерывны на . Тогда для 
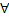точки 
и 
решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале .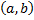
Рассмотрим левую часть ЛДУ (2.6.1) и (2.6.10) – дифференциальный оператор
.
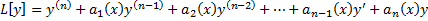Покажем, что 
является линейным оператором, т.е. 
и 
, где 
.
,
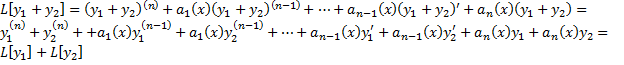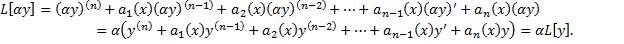
Таким образом, 
– линейный дифференциальный оператор.
Операторная форма ЛДУ:
ЛНДУ:
ЛОДУ:
Линейные однородные ДУ (ЛОДУ) n-го порядка.
Теорема. Множество частных решений ЛОДУ n-го порядка 
является линейным пространством относительно операций сложения функций и умножения на число.
Док-во. Нужно доказать, что операции сложения частных решений и умножения частных решений на число не выводит из множества частных решений, т.е. сумма частных решений 
– также решение, произведение частного решения на число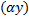 
– также решение, .
Пусть 
– решения, тогда 
, т.е. – решение, 
, т.е. 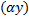– также решение. Нулевым вектором в линейном пространстве решений ЛОДУ является функция 
. 
Итак, решения ЛОДУ n-го порядка 
образуют линейное пространство.
Линейная зависимость функций. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций и о вронскиане системы линейно независимых частных решений ЛОДУ.
Опр. Функции 
называются линейно зависимыми на 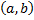, если 
, не все равные 
, такие, что 
Опр. Если выполнение равенства (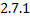
) на всем интервале 
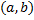возможно только при 
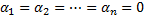, то функции 
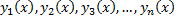называются линейно независимыми на .
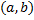Критерий линейной зависимости:
Функции линейно зависимы на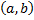 
для некоторого k=1,….n (т.е. хотя бы одна из функций линейно выражается через остальные).
Пример.
Т.к. 
, то функции линейно зависимы на 
Пусть функции 
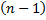раз дифференцируемы на .
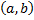Опр. Определителем Вронского (вронскианом) системы функций называется определитель
.
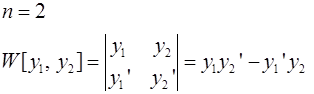
Теорема о вронскиане системы линейно зависимых функций
Пусть функции линейно зависимы на 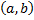. Тогда 
: 
Док-во: по определению линейной зависимости функций , не все равные , такие, что 
. Последовательно продифференцируем это равенство:
Зафиксируем 
(2.7.2) – СЛАУ (однородных) относительно 
, которая имеет ненулевое решение, т.е. определитель системы равен , т.е. (). 
Замечание. Обратное неверно, т.е. если 
, то функции могут быть линейно независимы.
Пример.
,
.
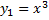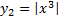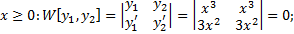
Т.е. 
на 
, но 
и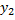 
линейно независимы, т.к. 
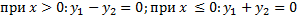. Не существует 
, таких, что 
для всех 
.