Аналого-цифровой преобразователь (аналог - код) предназначен для преобразования аналоговой величины в цифровой код. Схема АЦП зависит от метода преобразования и способа его реализации. Ряд схем АЦП содержит в своем составе ЦАП.
Существует ряд методов аналого-цифрового преобразования: последовательного счета; поразрядного уравновешивания; двойного интегрирования; с преобразованием напряжения в частоту; параллельного преобразования.
Наиболее часто используется метод поразрядного уравновешивания (последовательного преобразования), при этом последовательно формируются коды, начиная с цифры старшего разряда 2n-1 и завершая младшим (первым). Эти коды поступают на ЦАП, выход которого, сравнивается со входным сигналом.
 |
Рис. 3. Схема ЦАП
В схеме приняты следующие условные обозначения: РПП - регистр последовательных преобразований; ГТИ - генератор тактовых импульсов.
При нажатии кнопки пуск ГТИ заносит в старший разряд РПП единицу, при этом код преобразуется в аналоговый сигнал и сравнивается с входным сигналом - Uвх. В зависимости от выхода компаратора ГТИ записывает “1” в следующий разряд, а предыдущий разряд, либо оставляется без изменения, либо обнуляется.
В Фибоначчевых АЦП для поразрядного уравновешивания используются 1-числа Фибоначчи (1, 1, 2, 3, 5, 8,...).
Достоинство Фибоначчевых АЦП: избыточность кода Фибоначчи позволяет обнаруживать и исправлять ошибки при наличии помех.
Пример 1. В результате квантования по уровню значение сигнала выдается в двоичном коде с ценой младшего разряда равного шагу квантования. Определить необходимое число двоичных разрядов и количество уровней квантования при условии, что приведенная среднеквадратическая ошибка квантования не превышает 0,3%.
Решение: При заданном способе квантования погрешность квантования отрицательная и может принимать значения от 0 до Dx. Где Dx шаг квантования.
Среднеквадратическая ошибка квантования равна:

Приведенная среднеквадратическая ошибка квантования равна:

Если N - количество интервалов разбиения динамического диапазона изменения входного сигнала, то количество уровней квантования- m равно
 .
.
Количество двоичных разрядов двоичного кода
 .
.
Принимаем n = 7, т. е. для кодирования квантованного сигнала в двоичном коде, с ценой младшего разряда равного шагу квантования и точностью не ниже 0,3%, необходим семиразрядный двоичный код.
Пример 2. Случайный процесс с корреляционной функцией R(t) квантуется с шагом Dt. Найти погрешность представления такого процесса рядом Котельникова в зависимости от параметров a и Dt если

Решение: Спектральная плотность этого процесса равна

Определим погрешность, связанную с усечением спектра сигнала по формуле:

Найдем значения спектральных плотностей
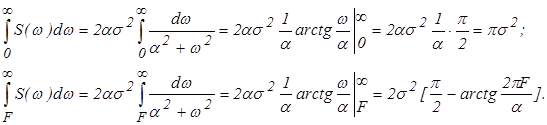
При этом выражение для погрешности усечения случайного сигнала имеет вид

Подставив значение F = 1/2Dt, определяемое в соответствии с теоремой Котельникова, найдем
 .
.
Если задана величина погрешности, можно определить шаг квантования.
Список Литературы
1. Быстродействующие интегральные микросхемы ЦАП и АЦП и измерение их параметров. Под редакцией Марцинкявючеса. М.: Радио и связь. 1988 –224с.
2. Валах В.В., Григорьев В.Ф., Быстродействующие АЦП для измерения формы случайных сигналов М.: Приборы и техника эксперемента. 1987. №4 с.86-90
3. Жан М. Рабаи, Ананта Чандракасан, Боривож Николич Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-ое изд. — М.: «Вильямс», 2007. — С. 912.
4. Угрюмов Е.П. Цифровая схемотехника.: Учебное пособие для вузов:-2-е издание, переработанное и дополненное-СПб: БХВ - петербург, 2005. - 800с.
5. Федерков Б.Г., Телец В.А., Микросхемы ЦАП и АЦП: функционирование, параметры, применение. М.: Энергоиздат, 1990. –320с.
6. Хоровиц П., Хилл У. Искусство схемотехники. В 3-х томах: Т. 2. Пер. с англ. — 4-е изд., перераб. и доп.— М.: Мир, 1993. — 371 с.