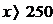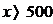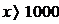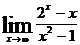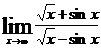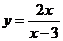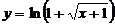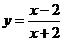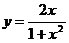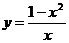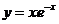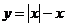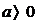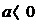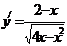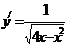Фонд тестовых заданий
По разделам дисциплины
Линейная алгебра с основами аналитической геометрии.
1. Определителем второго порядка, называется число 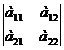
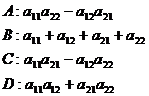
2. Вычислить определитель 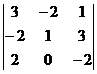
А. 14
В. –6
С. 4
D. –12
3. Найти матрицу 2А + 5В, если А= 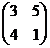 и B =
и B = 

4. Какие из приведенных формул являются формулами Крамера?
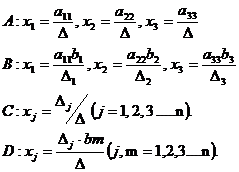
5. Скалярное произведение двух векторов определяется по формуле

6. Базисом векторного пространства Rn называется:
А: совокупность любых единичных векторов
В: совокупность n линейно зависимых векторов
С: совокупность n линейно независимых векторов
Д: совокупность независимого и единичного векторов
7.Сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом называется…
А: определённым интегралом
В: совокупностью элементов бесконечного множества
С: геометрической прогрессией
D: квадратичной формой L (x1, х2, …, хn)
8. Две прямые на плоскости параллельны если:
А: их угловые коэффициенты равны по величине, но противоположны по знаку k1 = -k2
В: обратны по величине, но равны по знаку k1 = 1/k2
С: равны по величине и по знаку k1= k2
Д: обратны по величине и противоположны по знаку k1 = - 1/k2
9. Множество всех точек плоскости, равностоящих от данной точки (фокуса) и от данной прямой представляет собой
А: параболу
В: гиперболу
С: любую плоскость
D: линию пересечения плоскостей
10. Среди прямых: а) Зх - 2у + 7 = 0; в) 6х + 4у -5 = 0;с) 2х + Зу -6 = 0 указать перпендикулярные.
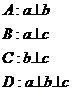
Математический анализ
1. Под областью определения функции подразумевается…
А: значение функции в определенном промежутке
В: все значения функции на некотором промежутке
С: совокупность промежутков монотонности
D: область допустимых значений независимой переменной «х».
2. Если для любого, сколь угодно малого положительного числа Е, найдется положительное число б > 0 (зависящее от Е), что для всех х, не равных Хо и удовлетворяющих условию | х - Xо | < б выполняется неравенство |f(x) - А|< Е, то число А называется...
А: пределом функции в бесконечности
В: производной функции
С: пределом функции в точке
Д: неопределенным интегралом от функции f (х)
3. Функция называется бесконечно малой если:
А: ее предел равен нулю
В: она не имеет предела
С: ее предел равен бесконечности
Д: ее предел равен единице
4. Найти первую производную функции у = х3arctg х

5. Функция называется непрерывной в точке Х0, если:
А: она определена в окрестности точки Х0, имеет предел в этой точке, этот предел равен значению функции в точке X0
В: она монотонно возрастает (или убывает) в точке Х0
С: она знакопостоянна и ограниченна в точке Х 0
Д: она не имеет предела в точке Х0
6. Производной функции у = f (х) в точке X0 называется:
А: неопределенный интеграл от дифференциала этой функции
В: предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю
С: предел суммы приращения функции и приращения аргумента
Д: предел неопределенного интеграла этой функции
7. Найти вторую производную функции у = cos х + 2х3 +1

8. Необходимый признак существования экстремума функции
А: существование первой производной
В: первая производная равна нулю или не существует
С: первая производная не существует
Д: вторая производная равна нулю
9. Если функция f (x) возрастает на некотором интервале, то на этом промежутке ее производная:
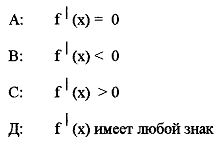
10. Какая из предложенных функций не изменяется при дифференцировании?

11. Уравнение касательной к кривой у = х2 в точке М (1/2; 1)
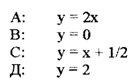
12. Неопределенный интеграл  - это
- это
А: интегральная сумма
В: совокупность производных от f(x)
С: угловой коэффициент касательной к кривой y=f(x)
Д: совокупность первообразных для f(x)
13. Чему равенò(1+2x) dx
14. Определенный интеграл  - это
- это
А: первообразная функции f (х)
В: производная функции f (х)
С: предел соответствующих интегральных сумм
Д: f(b)-f(a)
Теория вероятностей и математическая статистика
1. Какая вероятность приписывается достоверному событию?

2. Вероятность события равна 0,75. Чему равна вероятность противоположного события?

3. Три стрелка стреляют по цели. Вероятность попадания для первого стрелка - 0,75; для второго - 0,8; для третьего - 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.

4. Установлено, что вероятность выпадения дождя 1 октября в данном городе равна 1/7. Определить наивероятнейшее число дождливых дней 1 октября в данном городе за 40 лет.
А: 5 дней
В: 6 дней
С: 13 дней
Д: 33 дня
5 Какая из перечисленных ниже случайных величин является непрерывной:
А. Число попаданий в мишень при десяти независимых выстрелах
В. Отклонение от размера обрабатываемой детали от стандарта
С. Число нестандартных изделий, оказавшихся в партии из 100 изделий
Д. Число очков, выпавших на верхней грани при одном подбрасывании игрального кубика
6 Какой закон распределения имеет случайная величина, означающая число появления герба при одном подбрасывании монеты?
А. Биноминальный
В. Геометрический
С. Гипергеометрический
Д. Равномерный
7 Какой закон имеет случайная величина, означающая число появления герба при десяти подбрасываниях монеты?
А. Биноминальный
В. Геометрический
С. Гипергеометрический
Д. Равномерный
8 В коробке имеются 7 карандашей, из которых 4 карандаша – красные. Наудачу извлекаются 3 карандаша. Какой закон распределения имеет случайная величина, означающая число извлеченных красных карандашей?
А. Биноминальный
В. Геометрический
С. Гипергеометрический
Д. Равномерный
9 Математическое ожидание случайной величины Х, распределенной по биноминальному закону, вычисляется по формуле:
А. 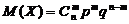
В. 
С. 
Д. 
10 Дисперсия случайной величины Х, имеющей геометрическое распределение, вычисляется по формуле:
А. 
В. 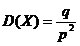
С. 
Д. 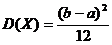
11 Значения случайной величины Х находятся в интервале 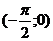 . Какая из функций может равняться на этом интервале функции распределения для Х?
. Какая из функций может равняться на этом интервале функции распределения для Х?
А. sin x
В. cos x
С. tg x
Д. ctgx
Итоговый контроль
1. Цена акций опустилась на 20%. На сколько она должна подняться, чтобы достичь предыдущего уровня?
- 20%
- 25%
- 30%
- 40%
2. Если  , то
, то 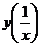 равно
равно
a. 
b. 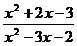
c. 
d. 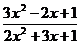
3. Постоянные издержки производства составляют 125 000 руб/месяц, переменные издержки – 700 рублей на единицу продукции, цена – 1200 рублей. При каком выпуске продукции х производство прибыльно?
4. Предприятие купило автомобиль за 200 000 рублей. Ежегодная амортизация составляет 20% от текущей стоимости. Какова цена автомобиля через 3 года в рублях?
a. 140000
b. 117200
c. 102400
d. 80000
5. Товарооборот фирмы увеличивается на 1% ежемесячно. Через сколько месяцев товарооборот увеличится в 2,7 раза?
- 270
- 100
- 27
- 10
6. Пусть объем выпускаемой продукции в зависимости от времени описывается функцией  . В какой момент времени производительность труда наибольшая?
. В какой момент времени производительность труда наибольшая?
- t=0
- t=3
- t=3,5
- t=4
7. 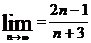 равен
равен
- 0
- 1
- 5
-
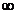
8. Правило Лопиталя нельзя применить для нахождения предела:
9. К какой из функций нельзя применить теорему Лагранжа на отрезке [0,2]?
10. Какая из функций убывает в любой точке своей области определения?
11. Какое из утверждений неверно:
- В точке экстремума производная равна нулю или не существует
- В точке экстремума производная меняет знак
- В точке экстремума функция меняет знак
- В точке, где производная равна нулю, может не быть экстремума
12. Из приведенных ниже функций горизонтальную асимптоту имеет
13. Какая из функций бесконечно малая при 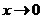 ?
?
-

-
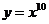 +1
+1 -

-

14. Требуется огородить прямоугольную площадку площадью 600 кв. м и разделить ее забором пополам. При каких размерах расход будет наименьшим?
- 60 м и 10 м
- 40 м и 15 м
- 30 м и 20 м
- 25 м и 24 м
15. Всегда верно утверждение:
- В точке перегиба всегда существует конечная 1-ая производная
- В точке перегиба всегда существует конечная 2-ая производная
- Точка перегиба – точка экстремума 1-ой производной
- Точка перегиба – точка экстремума 2-ой производной
16. Одного студента спросили, сколько ему лет? Ответ был замысловатым: возьмите трижды мои годы через 3 года, да отнимите мои годы 3 года назад, - у вас как раз и получатся мои годы. Сколько лет студенту?
- 17
- 18
- 19
- 20
17. Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 4 раза меньше?
- 1 кг
- 250 г
- 62,5 г
- 15,6 г
18. В студенческой группе 25 студентов. Из них хорошо знают математику 12 человек, историю – 16 человек и не знают хорошо этих предметов 4 человека. Сколько студентов в группе хорошо знают оба предмета?
- 4
- 7
- 8
- 9
19. Областью определения функции  является
является
- (-1;2)
- (-1;4]
- [-1;3]
- [1;3]
20. Множеством значений функции  является
является
- [0;1]
-

- [-2;2]
- [1;2]
21. Из приведенных ниже функций нечетной является
22. Указать все значения параметра а, при которых функция  при
при 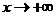 стремится к нулю
стремится к нулю
23. Предел числовой последовательности 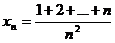 равен
равен
- 0
-
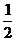
- 1
- 2
24. Найти производную функции 
25. Найти значение параметра b, при котором функция  имеет экстремум в точке х=-1.
имеет экстремум в точке х=-1.
- 0
- 1
- 2
- 3
26. Определителем второго порядка, называется число 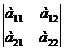
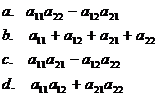
27. Вычислить определитель 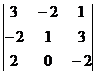
a. 14
b. –6
c. 4
d. –1
28. Найти матрицу 2А + 5В, если А= 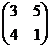 и B =
и B = 
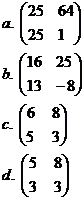
29. Какие из приведенных формул являются формулами Крамера?
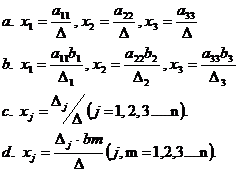
30. Скалярное произведение двух векторов определяется по формуле
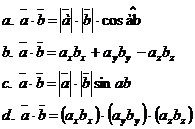
31. Базисом векторного пространства Rn называется:
a. совокупность любых единичных векторов
b. совокупность n линейно зависимых векторов
c. совокупность n линейно независимых векторов
d. совокупность независимого и единичного векторов
32. Сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом называется…
a. определённым интегралом
b. совокупностью элементов бесконечного множества
c. геометрической прогрессией
d. квадратичной формой L (x1, х2, …, хn)
33. Две прямые на плоскости параллельны если:
a. их угловые коэффициенты равны по величине, но противоположны по знаку k1 = -k2
b. обратны по величине, но равны по знаку k1 = 1/k2
c. равны по величине и по знаку k1= k2
d. обратны по величине и противоположны по знаку k1 = - 1/k2
34. Множество всех точек плоскости, равностоящих от данной точки (фокуса) и от данной прямой представляет собой
a. параболу
b. гиперболу
c. любую плоскость
d. линию пересечения плоскостей
35. Среди прямых: а) Зх - 2у + 7 = 0; в) 6х + 4у -5 = 0;с) 2х + Зу -6 = 0 указать перпендикулярные.
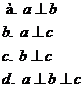
36. Три стрелка стреляют по цели. Вероятность попадания для первого стрелка - 0,75; для второго - 0,8; для третьего - 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.

37 Математическое ожидание случайной величины Х, распределенной по биноминальному закону, вычисляется по формуле:
А. 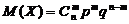
В. 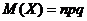
С. 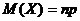
Д. 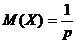
38 Значения случайной величины Х находятся в интервале 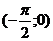 . Какая из функций может равняться на этом интервале функции распределения для Х?
. Какая из функций может равняться на этом интервале функции распределения для Х?
А. sin x
В. cos x
С. tg x
Д. ctgx
назад