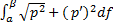Линейность и аддитивность определённого интеграла
I. Линейность определенного интеграла
Если функции f(x) и g (x) интегрируемы на отрезке [a, b], то при любых числах α, β О R функция α · f(x) + β · g(x) также интегрируема на [a, b] и справедливо равенство
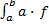(x)+ β·g(x) dx=a· 
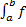(x)dx+ β· 
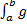(x)dx
II. Аддитивность определенного интеграла
а) Если функция f(x) интегрируема на отрезке [a, b] и a<c<b, то f (x) интегрируема на отрезках [a, c], [с, b] и справедливо равенство
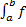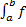(x)dx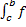= (x)dx+ 
(x)dx
б) Если функция f(x) интегрируема на отрезках [a, c] и [с, b], причем a<c<b, то f(x) интегрируема на отрезке [a, b] и справедливо равенство
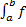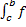(x)dx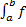+ (x)dx= (x)dx
Замечание. Примем, что
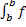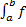(x)dx=- (x)dx
Тогда свойство II.б будет иметь место и без условия a<c<b:
Если функция f(x) интегрируема на отрезке [u, v], то при любом расположении точек a, b, c на отрезке [u, v] справедливо равенство
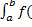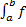x)dx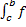= (x)dx+ (x)dx
Теорема про среднее значение определённого интеграла
Определенный интеграл от функции f(x), непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка:
(13). 
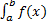dx=f(c)(b-a),a ≤c <b
Доказательство.
По свойству функций, непрерывных на отрезке f(x) достигает своего наименьшего m и наибольшего M значений и принимает все промежуточные значения между m и M:m≤f(x)≤M. В силу формулы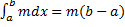 
, 
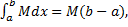предположив, что a<b, имеем
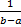
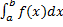m≤ 
≤M
Обозначим 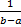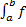(x)dx=K,K=const,тогда m≤ K M
По свойству непрерывных функций найдется значение x=c,(a≤c≤b) такое, что f(c)=K
Следовательно, из равенства 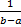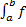(x)dx=f(c) (14)
получим нужное соотношение (13).
Замечание. В выражении (14) f(c) называют средним (средним интегральным) значением функцииf(x) на отрезке a≤x≤b.
|
|
Свойства интеграла как функции верхней грани
Рассмотрим функцию Ф(x)=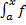 
(t)dt. Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.
Теорема 2.1. Если f(x) интегрируемая на [a,b] функция, то Ф(x) непрерывна на [a,b].
Доказательство. По свойству 9 определенного интеграла (теорема о среднем) имеем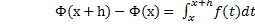 
=µh,откуда,при h 
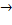0,получаем требуемое.
Теорема 2.2. Если f(x) непрерывная на [a,b] функция, то Ф’(x) = f(x) на [a,b].
Доказательство. По свойству 10 определенного интеграла (вторая теорема о среднем), имеем
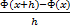=f(c),где с – некоторая точка отрезка [x,x+h]. В силу непрерывности функции f
получаем: Ф’(x)=l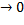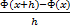im(h 
) lim(h 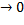)f(c)=f(x)
Таким образом, Ф(x) - одна из первообразных функции f(x) следовательно, Ф(x) = F(x) + C, где F(x) - другая первообразная f(x). Далее, так как Ф(a) = 0, то 0 = F(a) + C, следовательно, C = -F(a) и поэтому Ф(x) = F(x) – F(a). Полагая x=b, получаем формулу Ньютона-Лейбница
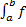(x)dx=Ф(b)=F(b)-F(a)
Применение определённого интеграла для вычисления длины кривой и объёма тела
Вычисление длины дуги плоской кривой
Пусть известна функция y=f(x) и требуется найти длину дуги, заданной функцией y=f(f), где
x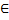 
[a,b].
Для определения длины дугиL необходимо вычислить определенный интеграл:
S=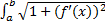 
dx
Рассмотрим случай параметрического задания кривой:
L: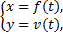 
Где t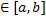 
. В этом случае для определения длина дуги вычисляется определенный интеграл:
S=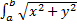 
dt=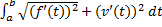 
Рассмотрим случай, когда кривая задается в полярных координатах p=(p(v) где,v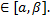 
Тогда для определения длины дуги L вычисляется следующий определенный интеграл:
S= 