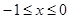Пусть α и β – две дуги, заключенные в промежутке от 0 до π/2 (первая четверть):
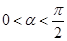 , и
, и 
Сумма α + β заключена в верхней полуокружности 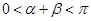 , следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:
, следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:
 ;
;

Разность α – β заключена в правой полуокружности: 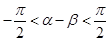
Следовательно, она может быть представлена в виде арксинуса, а также в виде арктангенса:
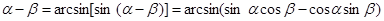 ;
;

Так как значение всякой аркфункции от положительного аргумента заключено в интервале (0; π/2) то сумму двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арккотангенса, а разность двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арктангенса.
Ниже приведены образцы соответствующих преобразований.
1. Преобразуем в арккосинус 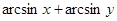 , где
, где 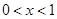 и
и 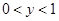
Имеем:
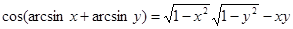
Откуда
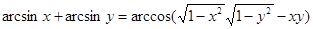
2. Аналогично
 , где 0 < x < 1, 0 < y < 1
, где 0 < x < 1, 0 < y < 1
 , где 0 < x < 1, 0 < y < 1
, где 0 < x < 1, 0 < y < 1



Формулы сложения аркфункций от произвольных аргументов.
1. Выразить сумму 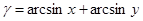 через арксинус
через арксинус
По определению арксинуса
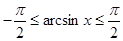 и
и 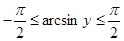 ,
,
откуда
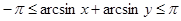
Для дуги γ возможны следующие три случая:
Случай 1: 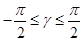
Если числа x и y разных знаков или хотя бы одно из них равно нулю, то имеет место случай 1.
В самом деле, при  и
и 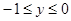 , имеем:
, имеем:
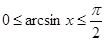 , и
, и 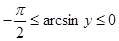 ,
,
откуда
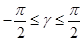
При x > 0, y > 0 для дуги γ имеет место одна из следующих двух систем неравенств:
а)  б)
б) 
Необходимым и достаточным признаком, позволяющим отличить один от другого случаи а) и б), является выполнение неравенства:
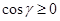 в случае а) и
в случае а) и 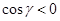 в случае б)
в случае б)
В самом деле, взаимно исключающие друг друга соотношения а) и б) влекут за собой взаимно исключающие следствия 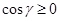 и
и 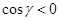 (соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.
(соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.
Вычислив  , получим:
, получим:
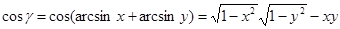
При x > 0, y > 0 наличие случая 1 означает выполнения неравенства а) т.е. 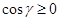 или
или
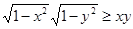
Откуда
 и, следовательно,
и, следовательно, 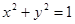
Наличие случая 1 при x < 0, y < 0 означает выполнение неравенств
 ;
;
но тогда для положительных аргументов –x и –y имеет место случай 1, а потому
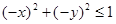 или
или 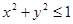
Случай 2. 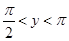
В этом случае x > 0, y > 0, т.е. выполняется неравенство б); из условия 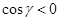 получим
получим 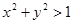
Случай 3. 
Этот случай имеет место при x < 0, y < 0, и 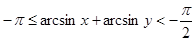
Изменив знаки на противоположные придем к предыдущему случаю:
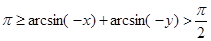
откуда 
Дуги γ и 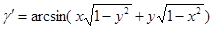 имеют одинаковый синус, но (по определению арксинуса)
имеют одинаковый синус, но (по определению арксинуса) 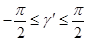 , следовательно в случае 1
, следовательно в случае 1  ;
;
в случае 2 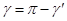 и в случае 3
и в случае 3 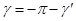 .
.
Итак, имеем окончательно:
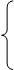
 ,
, 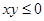 или
или 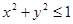
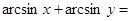
 ; x > 0, y > 0, и
; x > 0, y > 0, и  (1)
(1)
 ; x < 0, y < 0, и
; x < 0, y < 0, и 
Пример:
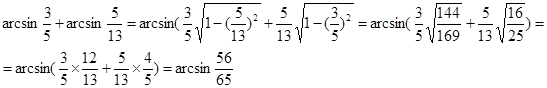
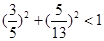 ;
; 
2. Заменив в (1) x на –x получим:

 ,
, 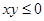 или
или 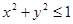

 ; x > 0, y > 0, и
; x > 0, y > 0, и  (2)
(2)
 ; x < 0, y < 0, и
; x < 0, y < 0, и 
3. Выразить сумму 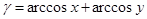 через арккосинус
через арккосинус
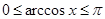 и
и 
имеем
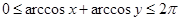
Возможны следующие два случая.
Случай 1: 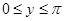 если
если  , то
, то
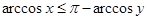
Приняв во внимание, что обе дуги 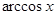 и
и 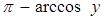 расположены в промежутке [0;π] и что в этом промежутке косинус убывает, получим
расположены в промежутке [0;π] и что в этом промежутке косинус убывает, получим

и следовательно, 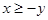 , откуда
, откуда 
Случай 2:  . Если
. Если 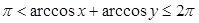 , то
, то
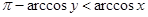 ,
,
откуда при помощи рассуждений, аналогичных предыдущим, получим 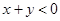 . Из сопоставления результатов следует, что случай 1 имеет место, если
. Из сопоставления результатов следует, что случай 1 имеет место, если 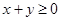 , а случай 2, если
, а случай 2, если
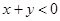 .
.
Из равенства 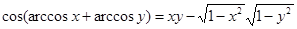 следует, что дуги
следует, что дуги
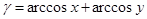 и
и  имеют одинаковый косинус.
имеют одинаковый косинус.
В случае 1  , в случае 2
, в случае 2 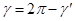 , следовательно,
, следовательно,


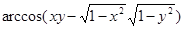 ,
, 
 ,
, 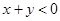 (3)
(3)
4. Аналогично
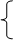
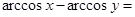
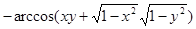 ,
, 
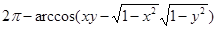 ,
, 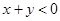 (4)
(4)
пример: 
5.

 ; xy < 1
; xy < 1
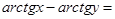
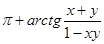 ; x > 1, xy > 1 (5)
; x > 1, xy > 1 (5)
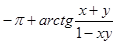 ; x < 0, xy > 1
; x < 0, xy > 1
При xy =1не имеет смысла
6.
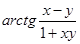 ; xy > -1
; xy > -1

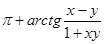 ; x > 0, xy < -1 (6)
; x > 0, xy < -1 (6)
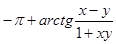 ; x < 0, xy < -1
; x < 0, xy < -1
7.
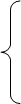
 ;
; 
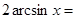
 ;
; 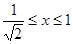 (7)
(7)
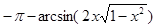 ;
; 
8.


 ;
;  (8)
(8)
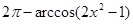 ;
; 
9.
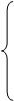
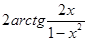 ;
; 

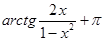 ; x > 1 (9)
; x > 1 (9)
 ; x < -1
; x < -1
10. 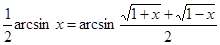 (10)
(10)
 (11)
(11)

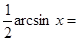
 , если
, если  (12)
(12)
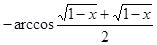 , если
, если