Рациональные сечения при изгибе

Деформации при чистом изгибе

При чистом изгибе в сечении возникает только один внутренний силовой фактор — изгибающий момент.

Рассмотрим деформацию бруса, нагруженного внешней паройсил с моментом т (рис. 32.1а).

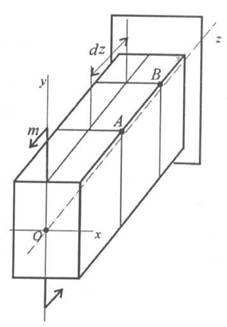Рис.

При чистом изгибе выполняются ги­потезы плоских сечений и ненадавливаемости слоев. Сечения бруса, плоские и перпенди­кулярные продольной оси, после дефор­мации остаются плоскими и перпенди­кулярными продольной оси. Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие. Действуют только нормальные на­пряжения. Поперечные размеры сечений не ме­няются. Продольная ось бруса после дефор­мации изгиба искривляется и образует дугу окружности радиуса р (рис. 32.16). Материал подчиняется закону Гука.

Можно заметить, что слои, расположенные выше продольной оси, растянуты, расположенные ниже оси — сжаты (рис. 32.16). Так как деформации по высоте сечения меняются непрерывно, имеется

слой, в котором нормальные напряжения о равны нулю; такой слой называют нейтральным слоем (НС). Доказано, нейтральный слой проходит через центр тяжести сечения; р — радиус кривизны ней­трального слоя.

Рассмотрим деформа­цию слоя, расположенного на расстоянии у от ней­тральной оси (участок АВ, рис. 32.1).

Длина участка до де­формации равна длине ней­тральной оси:

.

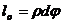Абсолютное удлинение слоя 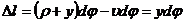(рис. 32.1б).

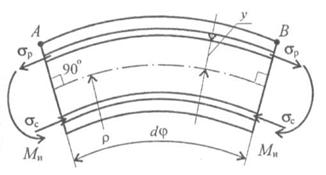Рис.	Относительное удлинение ; 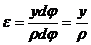. Относительное удлинение прямо пропорционально расстоянию слоя до нейтральной оси. Используем закон Гука при растяжении: σ = Еε. Получим зависимость нормального напряжения при изгибе

от положения слоя:

.

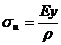Формула для расчета нормальных напряжений

При изгибе

Рассмотрим изогнутый участок бруса dz (рис. 32.2).

dN — элементарная про­дольная сила в точке сечения; dA — площадь элементарной площадки; dm — элементарный момент, образованный силой относитель­но нейтрального слоя. dN = σиdA; dm = σи ydA.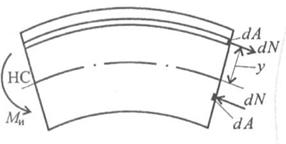

Рис.

Суммарный изгибающий момент сил упругости в сечении

.

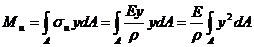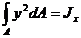- осевой момент инерции сечения.

Таким образом, .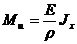

Откуда Е / р = M_n/ J_x. Ранее получено .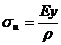

После ряда преобразований получим формулу для определения нормальных напряжений в любом слое поперечного сечения бруса:

,

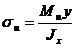где J_x — геометрическая характеристика сечения при изгибе.

Эпюра распределения нормальных напряжений при изгибе изо­бражена на рис. 32.3.

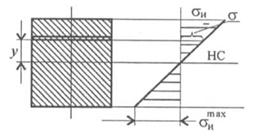Рис.	По эпюре распределения нор­мальных напряжений видно, что максимальное напряжение возника­ет на поверхности. Подставим в формулу напряже­ния значение у = уmax. Получим .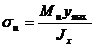

Отношение 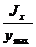принято обозначать W_x: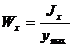

Эта величина называется моментом сопротивления сечения при изгибе, или осевым моментом сопротивления.

Размерность — мм³.

W_x характеризует влияние формы и размеров сечения на проч­ность при изгибе.

Напряжение на поверхности .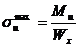

Рациональные сечения при изгибе

Определим рациональные сечения при изгибе, для этого срав­ним моменты сопротивления простейших сечений.

Осевой момент инерции прямоугольника (рис. 32.4) равен 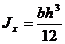. Осевой момент сопротивления прямо­угольника 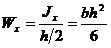. Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).

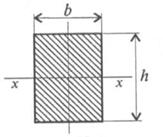Рис.

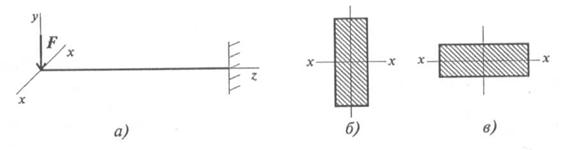
Рис.

Вариант на рис. 32.56 обладает большим сопротивлением изги­бу при прочих равных условиях.

Осевой момент инерции круга (рис. 32.6) равен .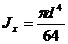

Осевой момент сопротивления круга .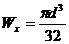

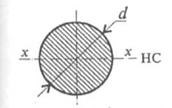Рис.

Все необходимые расчетные данные (площади, моменты инер­ции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1). Для материалов, одинаково работающих на растяжение и сжа­тие, выбирают сечения, симметричные относительно оси, вокруг ко­торой совершается изгиб (рис. 32.7).