Глава IX. Линейные операторы в унитарном и евклидовом пространстве
Везде в этой главе рассматриваются только евклидовы или унитарные
пространства.
Сначала сформулируем и докажем одно утверждение, которым будем пользоваться на протяжении всей этой главы.
Лемма 1. Пусть X – унитарное или евклидово пространство, 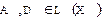 и для любых векторов
и для любых векторов 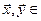 X справедливо равенство
X справедливо равенство  , или, что то же самое,
, или, что то же самое,
(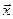 ,A
,A 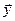 ) = (
) = (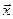 ,D
,D 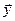 ). Тогда A =D.
). Тогда A =D.
Доказательство. Действительно, положив 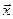 = (A –D)
= (A –D) 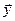 , получим: (
, получим: (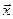 ,
, 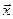 ) = 0. Из свойств скалярного произведения следует, что тогда
) = 0. Из свойств скалярного произведения следует, что тогда 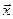 = (A –D)
= (A –D) 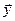 =A
=A 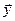 –D
–D 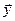 =
=  , или A
, или A 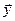 =D
=D 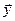 для любого
для любого
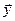 ÎX, что и доказывает равенство A =D.
ÎX, что и доказывает равенство A =D.
Сопряженный оператор.
Определение 1. Пусть X – унитарное или евклидово пространство,  . Оператор
. Оператор  называют сопряженным к оператору A, если для любых векторов
называют сопряженным к оператору A, если для любых векторов
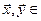 X справедливо равенство
X справедливо равенство 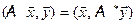 . (1)
. (1)
Замечание 1. Отметим, что равенство (1) эквивалентно следующему:
 . (2)
. (2)
Действительно, из свойств скалярного произведения и равенства (1) следует, что  , "
, " 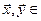 X. Таким образом, из равенства (1) следует (2). Аналогично доказывается, что из равенства (2) следует (1).
X. Таким образом, из равенства (1) следует (2). Аналогично доказывается, что из равенства (2) следует (1).
Замечание 2. Нетрудно доказать, что оператор  , удовлетворяющий равенству (1) для любых векторов
, удовлетворяющий равенству (1) для любых векторов 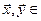 X, является линейным. Поэтому в определении 1 от требования линейности оператора
X, является линейным. Поэтому в определении 1 от требования линейности оператора  можно отказаться.
можно отказаться.
Замечание 3. Из определения 1, конечно, не следует существование оператора, сопряженного к данному.
Пример 1. Очевидно, 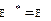 , т. к. для любых
, т. к. для любых 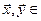 X имеем: (E
X имеем: (E 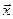 ,
, 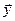 ) = (
) = (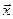 ,
, 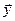 ) = (
) = (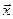 ,E
,E 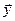 ).
).
Пример 2. Пусть  – пространство геометрических векторов плоскости, которое, как известно из линейной алгебры, является евклидовым пространством размерности 2.
– пространство геометрических векторов плоскости, которое, как известно из линейной алгебры, является евклидовым пространством размерности 2.
Легко доказать, что отображение  , сопоставляющее каждому вектору
, сопоставляющее каждому вектору  вектор, получающийся из
вектор, получающийся из 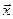 в результате поворота на угол j и растяжения в l раз (l Î R, l > 0), является линейным оператором.
в результате поворота на угол j и растяжения в l раз (l Î R, l > 0), является линейным оператором.
Покажем, что оператор  , сопоставляющий каждому вектору
, сопоставляющий каждому вектору 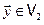 вектор, получающийся из
вектор, получающийся из 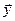 в результате поворота на угол –j и растяжения в l раз, является сопряженным к A.
в результате поворота на угол –j и растяжения в l раз, является сопряженным к A.
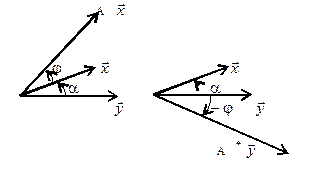 Рис. 1
Рис. 1
|
Нетрудно доказать, что  – линейный оператор. Легко видеть (рис.1), что для любых двух ненулевых векторов
– линейный оператор. Легко видеть (рис.1), что для любых двух ненулевых векторов 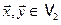 справедливы равенства
справедливы равенства
 ,
,
где  . Следовательно, для любых двух ненулевых векторов
. Следовательно, для любых двух ненулевых векторов 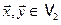 имеем:
имеем:
 .
.
Если хотя бы один из векторов 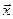 или
или 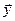 нулевой, то
нулевой, то  .
.
Таким образом, 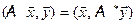 ,
,  и, следовательно, оператор
и, следовательно, оператор  является сопряженным к оператору A.
является сопряженным к оператору A.
Отметим, что если  – ортонормированный базис пространства X, то матрица оператора A в базисе
– ортонормированный базис пространства X, то матрица оператора A в базисе  имеет следующий вид:
имеет следующий вид:

Теорема 1. Для любого линейного оператора A, действующего в унитарном или евклидовом пространстве X, существует единственный сопряженный к нему оператор  .
.
Доказательство. 1. Докажем сначала существование оператора, сопряженного к A.
Пусть 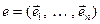 – ортонормированный базис пространства X и
– ортонормированный базис пространства X и  . По теореме 1 §3 главы YIII
. По теореме 1 §3 главы YIII
существует линейный оператор, который мы обозначим через  , такой, что
, такой, что  , т.е. если
, т.е. если  , то в i-й строке и j-м столбце матрицы
, то в i-й строке и j-м столбце матрицы  стоит элемент
стоит элемент  , где черта означает комплексное сопряжение.
, где черта означает комплексное сопряжение.
Покажем, что определенный таким образом линейный оператор  является сопряженным к A, т.е. для всех векторов
является сопряженным к A, т.е. для всех векторов 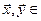 X справедливо равенство (1):
X справедливо равенство (1):
 ;
;
 .
.
Таким образом  для всех векторов
для всех векторов 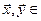 X. Следовательно, оператор
X. Следовательно, оператор  является сопряженным к
является сопряженным к  .
.
2. Теперь докажем, что такой оператор единственный. Пусть оператор  также удовлетворяет равенству (1), т.е.
также удовлетворяет равенству (1), т.е.  для всех векторов
для всех векторов 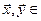 X. Тогда
X. Тогда 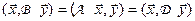 всех векторов
всех векторов 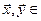 X. Следовательно, по лемме 1
X. Следовательно, по лемме 1  , и теорема доказана.
, и теорема доказана.
Оператор, сопряжённый к оператору  будем обозначать так:
будем обозначать так:  .
.
Следствие 1. Матрицы операторов A и  в любом ортонормированном базисе
в любом ортонормированном базисе  пространства X связаны соотношением
пространства X связаны соотношением  , т.е. матрица сопряжённого оператора в любом ортонормированном базисе является сопряжённой к матрице исходного оператора в том же базисе. В частности, если X – евклидово пространство, то
, т.е. матрица сопряжённого оператора в любом ортонормированном базисе является сопряжённой к матрице исходного оператора в том же базисе. В частности, если X – евклидово пространство, то  .
.
Следствие 2. Для любого оператора  справедливы равенства:
справедливы равенства:  ;
;  .
.
Доказательство. Пусть  – ортонормированный базис пространства X. По следствию к лемме 2 §4 главы YIII имеем:
– ортонормированный базис пространства X. По следствию к лемме 2 §4 главы YIII имеем:  ;
;  . Из определения ранга матрицы, свойств операции комплексного сопряжения и следствия 1 получаем:
. Из определения ранга матрицы, свойств операции комплексного сопряжения и следствия 1 получаем:
 .
.
Равенство для дефектов получается из уже доказанного, т.к. по теореме §4 главы YIII
 .
.
Следствие 3. Если  C является собственным числом матрицы
C является собственным числом матрицы  , то комплексно сопряжённое к нему число
, то комплексно сопряжённое к нему число  является собственным числом сопряжённой матрицы
является собственным числом сопряжённой матрицы  , т.е. если
, т.е. если
 , то
, то  .
.
Доказательство. Для любого  по теореме 1 §5 главы Y справедливо равенство
по теореме 1 §5 главы Y справедливо равенство  . Подсчитаем
. Подсчитаем
 ,
,
т.е.  . Это и означает, что
. Это и означает, что  для любого
для любого  .
.
Следствие 4. Если  C является собственным числом оператора
C является собственным числом оператора  , то комплексно сопряжённое с ним число
, то комплексно сопряжённое с ним число  является собственным числом сопряжённого оператора
является собственным числом сопряжённого оператора  , т.е. если
, т.е. если 
 , то
, то 
 .
.
Доказательство. Если 
 , то
, то 
 , где
, где  - ортонормированный базис X. Откуда с учётом следствий 1 и 3 получаем:
- ортонормированный базис X. Откуда с учётом следствий 1 и 3 получаем: 
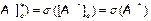 .
.
Теорема 2. Пусть X – унитарное или евклидово пространство. Для любых операторов 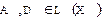 и любого числа
и любого числа  Î C справедливы следующие равенства:
Î C справедливы следующие равенства:
1. 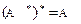 ;
;
2. 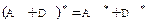 ;
;
3. 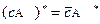 ;
;
4. 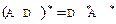 ;
;
5. Если A обратим, то обратим и оператор  , причём
, причём  .
.
Доказательство. Из свойств скалярного произведения и определения сопряженного оператора получаем, что для любых векторов 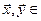 X справедливы равенства:
X справедливы равенства:
1.  ;
;
2. 
 ;
;
3.  ;
;
4.  .
.
Таким образом, из леммы 1 следует справедливость равенств 1 – 4.
5. Пусть теперь оператор A обратим, т.е. существует такой оператор  , что
, что  . Тогда получаем:
. Тогда получаем:  . По доказанному в пункте 4 последнее равенство можно переписать так:
. По доказанному в пункте 4 последнее равенство можно переписать так:  , что и означает обратимость сопряженного оператора
, что и означает обратимость сопряженного оператора  и справедливость равенства 5.
и справедливость равенства 5.
Теорема 3. Матрицы операторов A и  в произвольном базисе
в произвольном базисе  пространства X связаны соотношением
пространства X связаны соотношением
 .
.
В частности, если X– евклидово пространство, то  .
.
Дадим лишь несколько указаний для доказательства этой теоремы. Пусть  - ортонормированный базис пространства X. Тогда справедливы равенства:
- ортонормированный базис пространства X. Тогда справедливы равенства: 

 . Для завершения доказательства
. Для завершения доказательства
остаётся лишь показать, что  и что
и что  .
.
Теорема 4. Пусть X – унитарное или евклидово пространство. Для любого оператора  справедливы равенства
справедливы равенства  ,
,  .
.
Доказательство. Для любых векторов 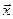 Î
Î  A и
A и 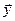 ÎX имеем:
ÎX имеем:  , или
, или  . Таким образом,
. Таким образом,  для любых
для любых 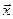 Î
Î  A. По определению ортогонального дополнения это и означает, что
A. По определению ортогонального дополнения это и означает, что  для любого
для любого 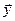 ÎX, или
ÎX, или  .
.
Покажем теперь, что  .
.
Действительно, 
Здесь мы воспользовались следствием 2 к теореме 1 и следствием 1 к теореме 1 §3 главы YIII. Таким образом,  . (3)
. (3)
Как следует из свойств ортогонального дополнения, тогда  .
.
Напишем равенство (3) для сопряженного оператора  :
:  . По теореме 2 это и означает, что
. По теореме 2 это и означает, что  .
.
Следствие. Для любого оператора  справедливы равенства
справедливы равенства
 ;
;  .
.
Доказательство. Оба разложения получаются из равенства  , которое справедливо для любого подпространства P (см. теорема 1 §3 главы YIII). В первом равенстве P = KerA, а во втором –
, которое справедливо для любого подпространства P (см. теорема 1 §3 главы YIII). В первом равенстве P = KerA, а во втором –  .
.
Самосопряженный оператор
Определение 1. Пусть X – евклидово или унитарное пространство. Оператор  называют
называют
самосопряженным, если  .
.
Если X – унитарное (евклидово) пространство, то самосопряженный оператор называют эрмитовым (симметричным).
Пример 1. Тождественный оператор E является самосопряженным, т.к. 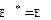 .
.