Определение 1. Пусть X – унитарное (евклидово) пространство. Оператор 
называют унитарным (ортогональным), если 
.
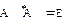Замечание 1. Из определения унитарного (ортогонального) оператора следует, что он обратим и что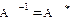 
.
Пример 1. Тождественный оператор, действующий в унитарном (евклидовом) пространстве, является унитарным (ортогональным), так как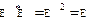 
.
Пример 2. Оператор A из примера 2 §1 является ортогональным, если l = 1, так как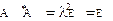 
.
Теорема 1. Пусть X – унитарное (евклидово) пространство. Для того чтобы оператор был унитарным (ортогональным), необходимо и достаточно, чтобы выполнялось одно из следующих условий:
1. Оператор A “сохраняет” скалярное произведение, т.е.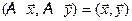 
для любых 
, 
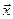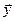ÎX.
2. Любой ортонормированный базис пространства X оператор A отображает в ортонормированный базис.
3. Оператор A “сохраняет” норму любого вектора 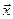ÎX, т.е. 
.
4. Матрица оператора A в любом ортонормированном базисе пространства X является унитарной (ортогональной).
Доказательство. 1.Необходимость. Пусть A – унитарный (ортогональный) оператор. Тогда по определению 1 справедливо равенство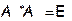 
. Следовательно, для любых векторов 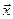, 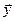ÎX имеем:
.
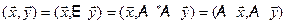Достаточность. Пусть для любых векторов 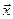, 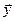ÎX справедливо равенство 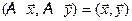. Тогда 
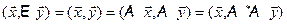, т.е. 
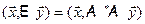для любых векторов 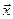, 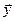ÎX.
Следовательно, по лемме 1 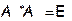, и A – унитарный (ортогональный) оператор. Здесь мы воспользовались ещё определением сопряженного оператора.
2.Необходимость. Пусть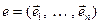 
– ортонормированный базис пространства X и 
.
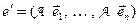Если A – унитарный (ортогональный) оператор, то по доказанному в пункте 1 имеем: 
для всех 
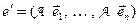. Следовательно, – ортонормированный базис.
Достаточность. Пусть теперь 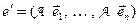– ортонормированный базис пространства X, т.е. 
для всех . Тогда для любых векторов 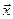, 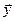ÎX имеем:
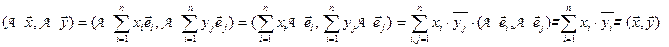.Следовательно, выполнены условия 1-го критерия, и оператор A – унитарный (ортогональный).
.
3. Необходимость. Если A – унитарный (ортогональный) оператор, то по доказанному в пункте 1 имеем: 
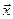, т.е. для любого ÎX.
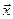Достаточность. Пусть теперь для любого ÎX. Покажем, что 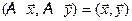для любых 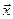, 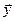ÎX. Из свойств скалярного произведения получаем: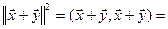 
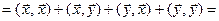
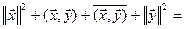
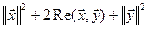, т.е.
(1) 
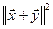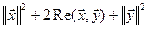= для любых векторов 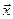, 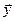ÎX..
Применив равенство (1) к вектору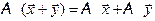 
, получим:
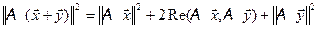(2)
Поскольку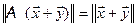 
, , 
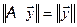, то из равенств (1) и (2) получаем:
.
Применив равенство (1) к вектору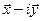 
, получим: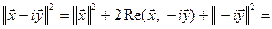 
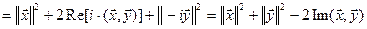, т.е.
= 
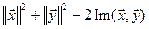(3)
и аналогично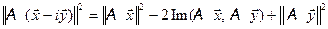 
(4)
Учитывая, что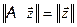 
, " 
ÎX, из равенств (3) и (4) получаем: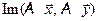 
= 
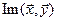. Итак,
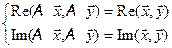для любых 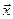, 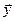ÎX.
Следовательно,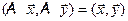 
для любых 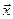, 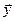ÎX, т.е. A – унитарный (ортогональный) оператор
в силу 1-го критерия.
4. Пусть 
– ортонормированный базис пространства X.
A – унитарный (ортогональный) оператор Û
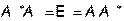Û 
Û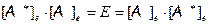 
Û
Û 
Û 
Û
Û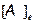 
– унитарная (ортогональная, если X – евклидово пространство). Теорема 1 полностью доказана.
Без доказательства приведём следующее утверждение.
Теорема 2. Для любого ортогонального оператора A, действующего в евклидовом пространстве X найдется ортонормированный базис , в котором матрица 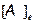имеет вид
.
Таким образом, геометрический смысл действия ортогонального оператора состоит в следующем. Пространство X раскладывается в ортогональную сумму одномерных и двумерных подпространств, на которых этот оператор действует так: на каждом одномерном подпространстве действие оператора состоит в умножении на 1 или на –1, а на каждом двумерном – в повороте на некоторый угол.