Какова бы ни была схема цепи, она может быть изображена в виде пассивного многополюсника, из которого выделены во внешние, относительно него, участки цепей источники воздействия и те пассивные элементы, отклики в которых подлежат определению.
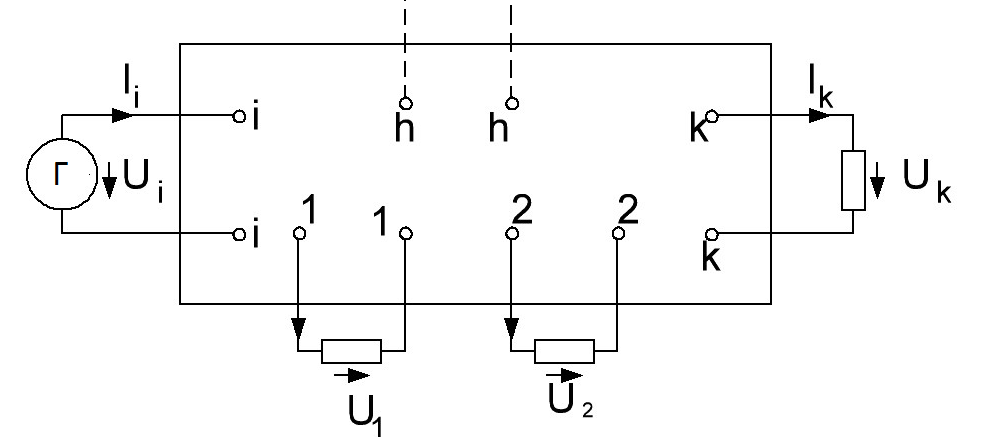
На схеме i-i – входные зажимы, так как к ним подключены генератор Г, определяемый своим напряжением 
или током 
.
Зажимы 1-1, 2-2, … h-h, k-k….. являются выходными, так как между ними могут быть включены внешние пассивные элементы.
Пусть цепь находится под гармоническим воздействием(напряжения или тока), выражаемым текущим комплексом 
. Источник воздействия включен между зажимами i-i.
Комплексной частотной характеристикой цепи (КЧХ) называется отношение текущих комплексов отклика и воздействия:
где 
, 
, а 
- амплитуды и начальные фазы отклика и воздействия.
или
Здесь
- АЧХ, определяет зависимость от частоты отношения амплитуд отклика и воздействия.
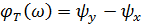- ФЧХ, выражает сдвиг фаз между откликом и воздействием как функцию частоты.
С другой стороны:
где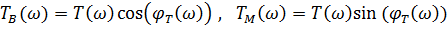 
- вещественная и комплексная части КЧХ/
Если 
уже известны, то можно определить:
Т.е. нет необходимости применять непосредственно правила Кирхгофа для расчета конкретного отклика.
Частотные функции классифицируются в зависимости от того, какие конкретные величины понимаются под воздействием и откликом. В частности функции подразделяются на входные и передаточные.
Пусть требуется определить отклик на входе цепи, т.е. ток при заданном напряжении .
Схема тогда сводится к двухполюснику:
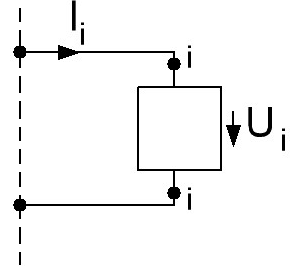Когда отклик и воздействие рассматриваются на одной паре зажимов i-i, то частотная характеристика называется входной. Она же является входным сопротивлением:
если - воздействие, а - отклик.
Полагая, что вся цепь питается только одним источником Э.Д.С., включенном в i-контуре, решаем систему уравнений метода контурных токов для этой схемы, имеем:
где 
, 
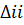- алгебраическое дополнение элемента 
в матрице 
.
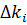- алгебраическое дополнение элемента 
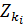в матрице .
Другая входная функция 
имеет размерность проводимости и совпадает с понятием входной проводимости цепи.
Формулы (*) и (**) позволяют рассчитывать входные функции сколь угодно сложной цепи.
Передаточные функции.
Когда требуется определить отклик на одном из выходов цепи(k-k) на воздействие источника, включенного на входе цепи (i-i), то схема может быть представлена в виде четырёхполюсника:
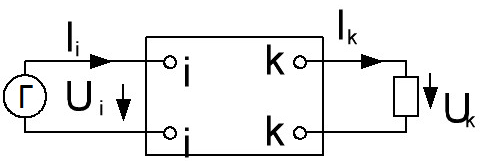
Комплексная частотная характеристика в таком случае называется передаточной.
Возможны 4-ре разновидности передаточных функций:
1) Передаточная проводимость.
- задано, определить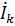 
.
Если для расчёта выбрано такое дерево, что ток 
равен контурному току, получим:
2) Передаточное сопротивление найти 
, задано .
- частотная передаточная характеристика, называемая передаточным сопротивлением.
Так как 
- то, учитывая (**), (***), получим
3) Передаточная функция по току это безразмерная функция:
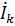- надо определить, - известно.
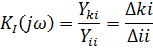
- комплексный коэффициент передачи по току.
4) Передаточная функция по напряжению?????????????? определение выходного напряжения по заданному входному напряжению 
- передаточная функция по напряжению.
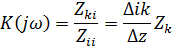
В случае относительно простых цепей для расчета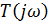 
необязательно прибегать к расчету определителей.
Принцип взаимности.
В соответствии с методом контурных токов для произвольной линейной цепи:
Отсюда, если в некотором i-ом контуре сложной цепи действует Э.Д.С. 
, то в другом (k-ом) контуре проходит ток: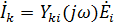 
, где передаточная проводимость:
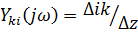
и дерево выбрано так, чтобы ток 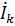равнялся контурному току k- контура.
№1
По отношению к схеме №1 рассмотрим дополнительную к ней:
Согласно схеме №2, Э.Д.С. перенесена из контура i в контур k, а зажимы, к которым она была подключена, замкнуты накоротко. При этом ток в i-ой ветви будет равен:
и отношение:
Перестановка индексов у общих сопротивлений не влияет на их величину: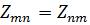 
. Поэтому определители 
и 
отличаются друг от друга тем, что строки одного совпадают со столбцами другого. Значит 
и 
.
На основании этого можно сформулировать следующий принцип взаимности:
Если Э.Д.С.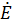 
, включенная в некотором участке А, сколь угодно сложной, цепи, не содержащей других источников энергии, создает ток 
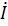в другом участке цепи В, то та же Э.Д.С., будучи включенной в участок В, вызовет в участке А тот же ток 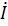. При переносе Э.Д.С., из одного участка цепи в другой, зажимы, к которым она была подключена, должны быть замкнуты накоротко.
На принципе взаимности основан метод взаимности, облегчающий в некоторых случаях анализ сложных цепей. Расчёт тока, создаваемого в участке А источником, включенным в участке В, может оказаться более простым, чем нахождение равного ему тока контура В, вызываемого источником, действующим в контуре А.
Пример. Основываясь на принципе взаимности, докажем равенство взаимных индуктивностей 
двух магнито-связанных катушек.
Э.Д.С. индуцируется во вторичном контуре, равна
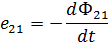
т.е. 
Аналогично: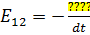 
Уравнения 2-го закона Кирхгофа для схемы имеют вид:
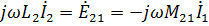
Решая эту систему, получим:
Перенесём Э.Д.С. из первого контура во второй, получим схему:
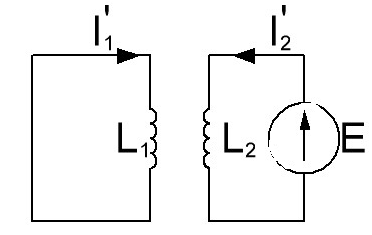
Для неё запишем систему уравнений Кирхгофа:
Отсюда находим:
На основании принципа взаимности:
