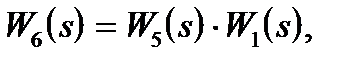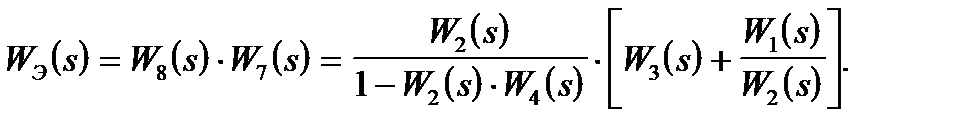Часто систему САУ можно рассматривать как комбинацию динамических звеньев с определёнными типовыми или нетиповыми передаточными функциями. Изображение системы регулирования в виде совокупности динамических звеньев с указанием связей между ними носит название структурной схемы. Элементы структурных схем приведены в таблице 1.
Структурная схема может быть составлена на основе известных уравнений системы, и наоборот, уравнения системы могут быть получены из структурной схемы. Однако первая задача может иметь различные варианты решения (различные структурные схемы для одной и той же математической модели САУ), тогда как вторая задача имеет всегда единственное решение.
Различные способы преобразования структурных схем облегчают определение передаточных функций сложных систем автоматического управления и дают возможность привести многоконтурную систему к эквивалентной ей одноконтурной.
Рассмотрим приведение к одному эквивалентному звену простейших сочетаний звеньев в структурных схемах.
а) Последовательное соединение звеньев (рис. 6)
Уравнения звеньев структурной схемы на рис. 6:
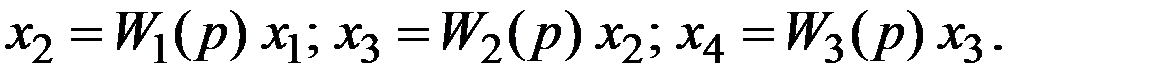 (21)
(21)
В результате взаимной подстановки выражений (21) получим уравнение эквивалентного звена (рис. 7): x 4= W 3(p) W 2(p) W 1(p) x 1.
Тогда передаточная функция эквивалентного звена Wэ= W 3(p) W 2(p) W 1(p).
б) Параллельное соединение звеньев (рис. 8)
Запишем уравнения элементов схемы, приведенной на рис. 8
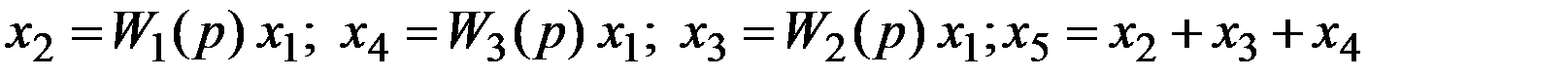 . (22)
. (22)
В результате исключения промежуточных переменных из уравнений (22) получим: 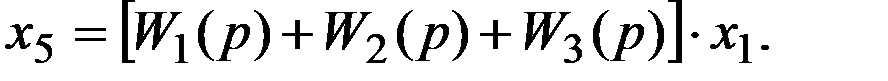
Таким образом, передаточная функция эквивалентного звена равна

в) Встречно-параллельное соединение звеньев (обратная связь) (рис.9).
Обратная связь может быть положительной, если сигнал 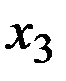 , снимаемый с выхода звена обратной связи, суммируется с сигналом
, снимаемый с выхода звена обратной связи, суммируется с сигналом 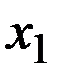 на входе (рис. 9 а), и отрицательной, если
на входе (рис. 9 а), и отрицательной, если 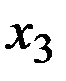 вычитается (рис. 9 б).
вычитается (рис. 9 б).
Для определения передаточной функции эквивалентного звена 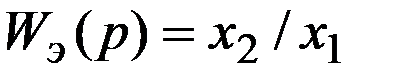 запишем следующие очевидные соотношения:
запишем следующие очевидные соотношения:

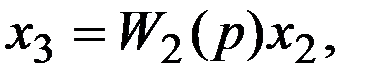 (23)
(23)
где знак плюс относится к положительной обратной связи, а знак минус – к отрицательной обратной связи.
Исключим из выражений (23) переменную 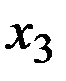 , подставив второе выражение в первое:
, подставив второе выражение в первое:  (24)
(24)
Решив уравнение (24) относительно  , найдем передаточную функцию эквивалентного звена
, найдем передаточную функцию эквивалентного звена
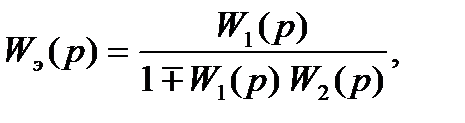 (25)
(25)
Здесь знак минус относится к положительной обратной связи, а знак плюс – к отрицательной обратной связи.
Если в одной из ветвей структурных схем, приведенных на рис. 9, нет звена (рис. 10), это означает, что передаточная функция данной ветви равна единице. Для варианта схемы, приведенной на рис. 10а, имеем 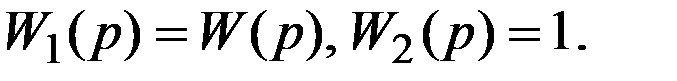 Формула (25) для этого случая примет вид:
Формула (25) для этого случая примет вид:
 (26)
(26)
Для варианта схемы, приведенной на рис. 10 б, соответственно получим:
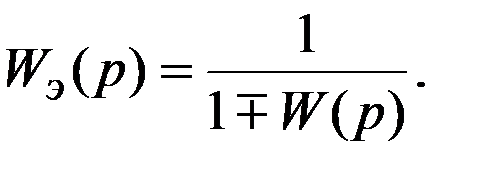 (27)
(27)
ЗАДАНИЕ 2
Определить передаточную функцию САУ. Варианты заданий приведены ниже.
1)
2)
3)
4)
5)
Иногда при преобразовании структурной схемы для выделения типовых соединений возникает необходимость переноса узла или сумматора. В этом случае перенос осуществляется по следующим правилам:
а) перенос узла с выхода звена на его вход:

исходная схема эквивалентная схема
Рис. 11. Перенос узла с выхода звена на его вход.
б) перенос узла с входа звена на его выход:

исходная схема эквивалентная схема
Рис. 12. Перенос узла с входа звена на его выход.
в) перенос сумматора с выхода звена на его вход:

исходная схема эквивалентная схема
Рис. 13. Перенос сумматора с выхода звена на его вход.
г) перенос сумматора с входа звена на его выход:

исходная схема эквивалентная схема
Рис. 14. Перенос сумматора с входа звена на его выход.
В качестве примера рассмотрим структурную схему объекта:

Рис. 15. Структурная схема объекта.
Для выполнения преобразования необходимо перенести узел со входа звена W2(s) на его выход. Схема примет вид:

Рис. 16. Структурная схема объекта.
 .
.
Заменяем эквивалентными звеньями последовательно соединенные звенья W5(s) и W1(s)
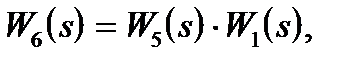
параллельно соединенные звенья W6(s) и W3(s)

а также звено W2(s), охваченное положительной обратной связью

Получим последовательно соединенные звенья с передаточными функциями W8(s) и W7(s).

Рис. 17. Эквивалентная передаточная функция объекта.
Эквивалентная передаточная функция объекта примет вид:
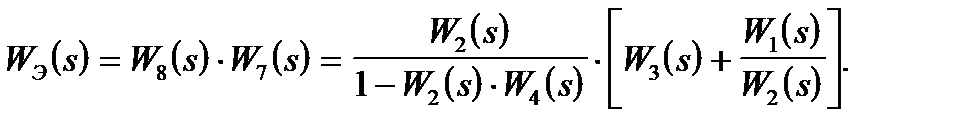
ЗАДАНИЕ 3
Преобразовать структурную схему САУ путем переноса сумматора. Варианты задания приведены ниже.
1)
2)
3.
ЗАДАНИЕ 4.
Преобразовать структурную схему САУ путем переноса узла. Варианты задания приведены ниже.
1)
2)
Преобразовать структурную схему САУ путем переноса узла
ЗАДАНИЕ 5.
Определить передаточную функцию САУ, предварительно преобразовав ее структурную схему. Варианты задания приведены ниже.
1)
2)
3)


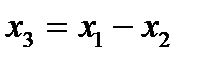
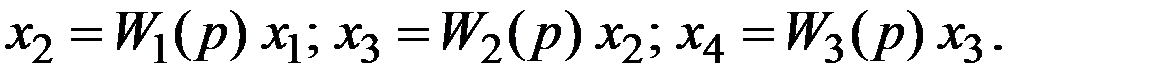 (21)
(21)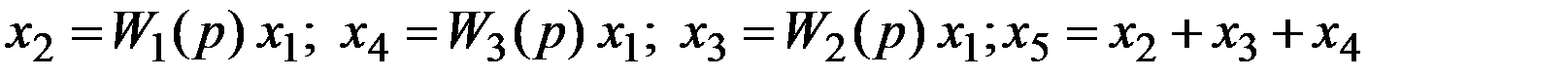 . (22)
. (22)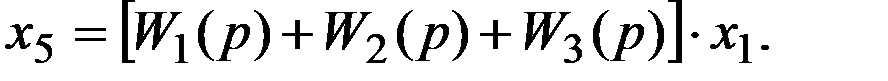

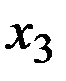 , снимаемый с выхода звена обратной связи, суммируется с сигналом
, снимаемый с выхода звена обратной связи, суммируется с сигналом 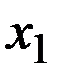 на входе (рис. 9 а), и отрицательной, если
на входе (рис. 9 а), и отрицательной, если 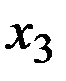 вычитается (рис. 9 б).
вычитается (рис. 9 б).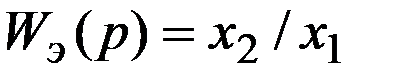 запишем следующие очевидные соотношения:
запишем следующие очевидные соотношения:
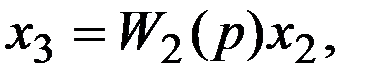 (23)
(23)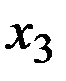 , подставив второе выражение в первое:
, подставив второе выражение в первое:  (24)
(24) , найдем передаточную функцию эквивалентного звена
, найдем передаточную функцию эквивалентного звена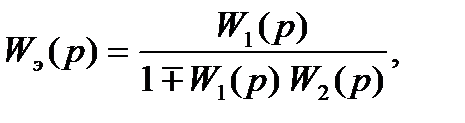 (25)
(25)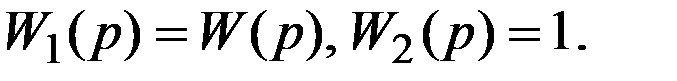 Формула (25) для этого случая примет вид:
Формула (25) для этого случая примет вид: (26)
(26)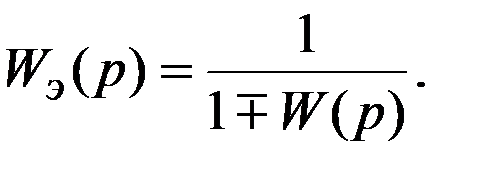 (27)
(27)





 .
.