ЛАБОРАТОРНАЯ РАБОТА № 1. МОДЕЛИРОВАНИЕ СИСТЕМЫАВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Объект управления (ОУ) — система, в которой происходит подлежащий управлению процесс. Взаимодействие с ОУ происходит через входы (которые являются причинами появления процессов в ОУ) и выходы (которые являются процессами-следствиями).
Управление — процесс на входе объекта управления, обеспечивающий такое протекание процессов на выходе объекта управления, которое обеспечи-вают достижение заданной цели управления.
Регулирование — частный случай управления, цель которого заключается в поддержании на заданном уровне одного или нескольких выходов объекта управления.
Система автоматического регулирования (САР) – совокупность объекта управления и автоматического регулятора, взаимодействующих между собой в соответствии с алгоритмом управления.
Регулирующий орган (РО) — совокупность устройств, с помощью кото-рых осуществляется управление входами объекта управления. Например, на-гревательные элементы в системе управления температурой, клапаны с элек-троприводом в системе регулирования расхода жидкости и т.д.
Управляемая величина (выходная величина - У) — показатель технологического процесса, которым необходимо управлять.
Управляющее воздействие (входная величина - Х) - физическая величина, посредством которой управляется показатель технологического процесса.
Задающее воздействие — определяет требуемый закон регулирования выходной величины.
Возмущающее воздействие f(t) — процесс на входе объекта управления,являющийся помехой управлению.
Воспринимающие органы (ВО или так называемые чувствительные эле-менты ЧЭ) - измеряют и преобразуют контролируемую или управляемую вели-чину объекта управления в сигнал, удобный для передачи и дальнейшей обра-ботки. К ним относятся датчики влажности, температуры (термопары, термосо-противления, термопреобразователи), освещенности и т.д.
Усилительные органы (УО или усилительные элементы УЭ) – устройства, не изменяющие физической природы сигнала, а производящие только усиление, т.е. увеличение его до требуемого значений. Сюда относятся магнитные пускатели, твердотельные и электромагнитные реле и т.д.
Преобразующие органы (ПО или элементы ПЭ) - преобразуют сигнал од-ной физической природы в сигналы другой физической природы для удобства дальнейшей передачи и обработки. Например, преобразователи неэлектрических величин в электрические.
Корректирующие органы (КО или элементы КЭ) - служат для коррекции САУ с целью улучшения их работы.
Исполнительный орган (ИО или элемент ИЭ) - вырабатывает и подает на регулирующий орган объекта управления управляющее воздействие.
Перечисленные выше термины поясняет рисунок 1, на котором изображе-на система автоматического управления (САУ), объектом управления которой является водонагреватель.
| Нагретая вода |
| Вода |
| R |
| U |
| tводы |
| Р |
| Управляющее воздействие Х (напряжение питания) |
| Задающий орган (ограничивающее сопротивление) |
| Возмущающее воздействие (температура окружающего воздуха) |
| Регулирующий орган (нагревательный элемент) |
| Управляемая величина У (температура воды) |
| Tокр |
Рисунок 1 - Водонагреватель как объект управления (Р - мощность нагревательного элемента)
Чаще всего объекты управления изображают графически в виде функ-циональных блоков (рис. 2).
| ЗО |
| PОУ |
| ОУ |
| R |
| U |
| P |
| tводы |
| tводы |
| tводы |
U - управляющее воздействие (напряжение питания),
Р – мощность нагревательного элемента,
tокр - возмущающее воздействие (температура окружающего воздуха),
tводы - управляемая величина (температура воды),
РОУ - регулирующий орган (нагревательный элемент),
ОУ - объект управления водонагреватель),
ЗО - задающий орган (ограничивающее сопротивление).
Рисунок 2 – Водонагреватель в виде функциональных блоков
ПРЕДСТАВЛЕНИЕ САУ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ И ПЕРЕДАТОЧНОЙ ФУНКЦИЕЙ
САУ может быть смоделирована (представлена) дифференциальным уравнением. При составлении дифференциального уравнения объекта необходимо прежде всего выявить физический закон (или совокупность законов), определяющий его поведение. Таким законом может быть, например, закон сохранения энергии, закон равновесия электродвижущих сил и другие основные законы физики. Математическое выражение соответствующего физического закона и является исходным дифференциальным уравнением управляемого объекта.
Очень важной категорией в теории автоматического управления и регулирования является понятие передаточной функции. Передаточная функция является своего рода математической моделью САУ, т.к. полностью характеризует динамические свойства системы.
Под передаточной функцией элемента или системы понимают отношение операторного (лапласового) изображения соответствующей выходной величины к операторному изображению входной величины.
При этом также считают, что элемент или система находились при нулевых начальных условиях, т.е. элемент или система находились в установившемся состоянии, т.е. в состоянии покоя.
Следовательно, передаточная функция определяется в виде отношения (1):
(1)
Предположим, что линейная САУ описывается дифференциальным уравнением n-го порядка с постоянными коэффициентами и это уравнение имеет следующий вид:
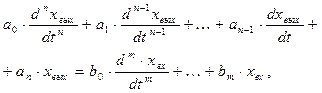(2)
где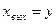 
- выходная величина звена (системы);
- входная величина звена (в отклонениях от состояния равновесия);
, 
- постоянные коэффициенты, определяющие параметры звена.
При записи дифференциального уравнения члены, содержащие выходную величину и её производные, записывают в левой части уравнения, а все остальные члены – в правой.
Запись уравнения в форме (2) неудобна, особенно когда возникает необходимость исследовать взаимодействие отдельных звеньев системы при их соединении в различные цепи. Кроме того, решения уравнений с порядком выше третьего значительно усложняется и требует применения вычислительной техники. Поэтому для упрощения решения уравнения (2) используют средства описания динамических свойств системы через преобразование Лапласа. Основанием для этого служит то обстоятельство, что такое преобразование существенно облегчает исследование сложных систем, поскольку дифференциальные уравнения заменяются алгебраическими.
Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оргигинала) называется функция:
(3)
f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа. f(x) и F(p) однозначно определяются друг относительно друга, то есть если известен оригинал f(x), то всегда можно узнать F(p), и наоборот, если известно F(p), то всегда можете получить f(x).
Преобразование Лапласа для типовых математических операций, а также для функций, часто встречающихся в задачах автоматического регулирования можно найти в учебниках.
Пользуясь преобразованием Лапласа, представим дифференциальное уравнение (2) в операторном виде:
(3)
или
(4)
где
(5)
есть оператор дифференцирования.
Для системы, описываемой операторным уравнением (4) передаточная функция будет иметь следующий вид:
(6)
Следовательно, передаточная функция 
равна отношению двух полиномов:
(7)
(8)
Как видно из уравнения (6), передаточная функция является дробно-рациональной функцией от независимого переменного p. Числитель передаточной функции является левой частью уравнения элемента или системы, а знаменатель - правой частью.
Уравнение
(9)
называется характеристическим уравнением звена или характеристическим полиномом звена.
В системах автоматического управления степень полинома знаменателя в выражении (6) всегда выше или равна степени полинома числителя, т.е. 
.
Из приведенных соотношений также видно, что передаточную функцию легко получить из дифференциального уравнения простой формальной заменой производных оператором р в соответствующей, а изображение выходной величины определяется передаточной функцией и изображением входной величины:
(10)
Запись соотношений между выходом и входом звена в виде последнего уравнения (10) имеет большое практическое значение и дает значительное преимущество при исследовании САР, т.к. оно позволяет графически изобразить звено следующим образом
Рис. 3 – Графическое изображение звена
В замкнутых САР имеется сложное взаимодействие блоков: выход одного блока может служить входом другого блока и т.д. Использование понятия передаточной функции звеньев позволяет без особого труда находить связь между любыми координатами всей системы на основании знания передаточных функций соответствующих звеньев, составляющих эту систему. Не представляет трудности при этом и составление общего графического изображения ее в виде структурной системы.
Рассмотрим также в общем виде очень важное понятие коэффициента передачи (коэффициента усиления) К в установившемся режиме для звена с произвольной передаточной функцией W(р).
Если на вход звена подать постоянный входной сигнал Хвх.у, то выходной сигнал Хвых.(t) при t → ∞, будет стремится к некоторому установившемуся значению
. (11)
Тогда по определению
(12)
Или считая, что в установившемся режиме все производные становятся равными нулю, получим выражение для передаточной функции (2.9.)
(13)
Следовательно, при р = 0 передаточная функция вырождается в обычный коэффициент усиления элемента или системы.
Представим математическое описание и передаточную функцию для R-L цепи, представленной на рис.4
Рис. 4 – Схема R-L цепи
Для R-L цепи можно представить следующее дифференциальное уравнение
(14)
(15)
Решив уравнение (15) относительно тока i и подставив в уравнение (14), получим
(16)
или
(17)
Где
– постоянная времени RL-цепи.
Представим уравнение (16) в операторном виде
(18)
или
(19)
Отсюда передаточная функция данного звена будет иметь вид
(20)
Графически это звено изобразится как показано на рис. 5.
Рис.5 – Графическое изображение звена
ЗАДАНИЕ 1
Определить передаточную функцию САУ и коэффицент передачи
Варианты заданий
1) 4 y'' + 3 y' + y = 7 x'
2) 2 y'' + y = 3 x'
3) 5 y'' + y' = 2 x'
4) 3 y'' + 7 y' + y = 9 x'
5) 6 y'' + 8 y' + y = 4 x'
6) 2 y'' + 3 y' + y = x'
7) 5 y'' +6 y = 4 x'
8) 3 y'' +7 y' = 6 x'
9) 6 y'' + 2 y' + 8 y = x'
10) 4 y'' + 2 y' +9 y = 5 x'
11) 9 y'' + 8 y' +10 y =10 x'
12) 7 y'' +6 y = 8 x'
13) 10 y'' +6 y' = 7 x'
14) 8 y'' + 12 y' + 6 y = 13 x'
15) 11 y'' + 13 y' +6 y = 10 x'