Содержание
Введение………………………………………………………………………………...
1. Метод интерполяций…………………………………………………….
1.1 Метод неопределенных коэффициентов построения интерполяционного полинома………………………………………………………………………
1.2 Интерполяционный полином в форме Ньютона…………………………...
1.3 Интерполяционный полином в форме Лагранжа…………………………..
1.4 Результаты и графики………………………………………………………..
2. Методы численного интегрирования…………………………………...
2.1. Метод прямоугольников……………………………………………………….
2.2. Метод трапеций………………………………………………………………...
2.3. Метод парабол (метод Симпсона)…………………………………………….
2.4. Результаты и график…………………………………………………………...
3. Заключение……………………………………………………………….
4. Список использованной литературы…………………………………...
Введение
Интерполяция, интерполирование — это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Точное нахождение первообразной (или интеграла) произвольных функций — это процедура более сложная, чем «дифференцирование», то есть нахождение производной. Зачастую, выразить интеграл в элементарных функциях невозможно.
|
|
Существуют различные методы интерполирования и интегрирования, в данной расчетно-графической работе будут рассмотрены некоторые из этих методов.
Методы интерполяций.
| Решение задачи методами интерполирования предполагает выполнение условия | ||
 при 
| (1) | |
| Интерполяционный алгебраический полином имеет вид | ||
| (2) | |
Задача (1) имеет решение, если степень полинома n = m-1, где m - количество точек интервала [a,b], в которых задана функция f(x). Таким образом, многочлен n- ой степени может обеспечить совпадение с приближаемой функцией f(x) в (n+1) точке конечного интервала. Однако, поведение разности P(x) - f(x) в точках  и  при построении полинома не оговаривается. При определённых ограничениях, накладываемых на f(x), и разумном выборе координат узлов сетки xi величина  . Выполнением этого условия определяется свойство равномерной сходимости интерполяционного процесса. Можно показать, что величина уклонения 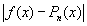 , зависит, в частности, от расположения узлов интерполяции xi на интервале [ a,b ]. Близкой к оптимальной, в смысле минимума функции  , при , является, так называемая, чебышевская сетка. Координаты её узлов определяются выражением
| ||
| (3) |
Эта сетка обладает рядом замечательных свойств. Так, если функция f(x) обладает непрерывной первой производной, то интерполяционный процесс на чебышевской сетке всегда сходится. Эта сетка также позволяет:
- построить интерполяционный полином близкий к полиному наилучшего равномерного приближения и
- обеспечивает, в сравнении с равномерной сеткой, существенно более высокую устойчивость полинома к погрешностям задания исходных данных.
Однако, следует иметь в виду, что достоинства этой сетки не предопределяют абсолютную целесообразность её использования.
|
|
Методы численного интегрирования
Метод прямоугольников
Идея численного интегрирования предельно проста и вытекает из геометрического смысла определенного интеграла – значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции y=f(x), осью абсцисс и прямыми х=а, х=b. Находя приближенно площадь криволинейной трапеции, мы получаем значение интеграла. Формально процедура численного интегрирования заключается в том, что отрезок [а, b] разбивается на n частичных отрезков, а затем подинтегральная функция заменяется на нем легко интегрируемой функцией, по определенной зависимости интерполирующей значения подинтегральной функции в точках разбиения. Рассмотрим теперь простейшие из численных методов интегрирования.
Итак, функция у=f(x) интегрируема на сегменте [a,b] и требуется вычислить ее интеграл 
. Составим интегральную сумму для f(x) на сегменте [a,b]. Для этого разобьем сегмент [a,b] на n равных между собой частей с помощью точек: x1, x2, …, xk, …, xn-1.
Если длину каждой части мы обозначим через 
х, так что 
, то для каждой точки xk будем иметь: 
(k=0, 1, 2, …, n).
Обозначим теперь через yk значение подынтегральной функции f(x) при 
то есть положим 
(k=0, 1, …, n).
Тогда суммы 
будут интегральными для функции f(x) на отрезке [a,b]. (При составлении первой суммы мы рассматриваем значения функции y=f(x) в точках, являющихся левыми концами частичных сегментов, а при составлении второй суммы – в точках, являющихся правыми концами этих сегментов.)
|
|
По определению интеграла имеем:
и 
Заключение
В данной расчетно-графической работе №1 были изучены методы интерполирования (Метод неопределенных коэффициентов построения интерполяционного полинома, Интерполяционный полином в форме Ньютона, Интерполяционный полином в форме Лагранжа) и интегрирования (Метод прямоугольников, Метод трапеций, Метод Симпсона). Нашли значение теплофизической величины в заданной точке методами линейной интерполяции и полиномиальной интерполяции с помощью программы Microsoft Office Excel, а также нашли численное значение интеграла для n = 10, используя метод трапеций и метод Симпсона с помощью программы Pascal.
Список использованной литературы:
1. Борисова Н.Г. Компьютерные технологии в теплоэнергетических расчетах. Конспект лекций для студентов всех форм обучения специальности 050717-Теплоэнергетика. - Алматы: АИЭС, 2010. – 57 с.
2. Борисова Н.Г. Компьютерные технологии в теплоэнергетических расчетах. Методические указания к выполнению лабораторных работ. – А.: АИЭС, 2005. -36с.
3. Численные методы теплофизики/Под ред. А.С.Аскаровой и др.-А.: «Қазақ университеті», 2008,9
4. Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании. - М.: ВШ, 2001. - 256 с.