Некоторые методы решения логарифмических уравнений.
Настоящая статья содержит систематическое изложение методов решения логарифмических уравнений с одной переменной. Это поможет учителю, прежде всего в дидактическом смысле: подбор упражнений позволяет составить для учащихся индивидуальные задания с учетом их возможностей. Данные упражнения могут быть использованы для урока обобщения и для подготовки к ЕГЭ.
Краткие теоретические сведения и решения задач позволяют учащимся самостоятельно развивать умения и навыки решения логарифмических уравнений.
Решение логарифмических уравнений.
Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма.
При решении логарифмических уравнений часто используются теоретические сведения:
а) log 
c = b, 
= c; 
>0, ≠ 1, c >0.
б) Если log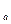 
х = log 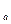у, где >0, ≠ 1, х>0, у>0, то х = у.
в) Если α >0, ≠ 1, х>0, у>0, то
1. 
2. 
3. log 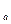(ху) = log 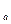х + log 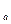у;
4. log 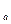(х / у) = log 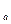х - log 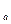у;
5. log х 
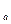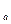= к ∙ log х; 
6. log 
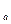х = 1/ к ∙ log х;
7. 
8. 
9. 
, где b > 0, с > 0;
10. log 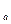х ∙ log 
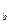у = log 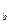х ∙ log 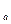у, где b ≠ 1, b > 0.
Обычно решение логарифмических уравнений начинается с определения ОДЗ. В логарифмических уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания были равны. Затем уравнения либо выражают через один какой – либо логарифм, который обозначается новой переменной, либо уравнение преобразовывают к виду, удобному для потенцирования.
Преобразования логарифмических выражений не должны приводить к сужению ОДЗ, если же примененный метод решения сужает ОДЗ, выпуская из рассмотрения отдельные числа, то эти числа в конце задачи необходимо проверить подстановкой в исходное уравнение, т.к. при сужении ОДЗ возможна потеря корней.
1. Уравнения вида log 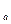f(х) =b, f(х) >0 – выражение, содержащее неизвестное число, а число >0, ≠ 1.
Для решения таких уравнений надо:
1) воспользоваться определением логарифма: f(х) = ;
2) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
Если log 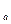f(х) =b, то f (х) = , > 0, ≠ 1).
2. Уравнения первой степени относительно логарифма, при решении которых используются свойства логарифмов.
Для решения таких уравнений надо:
1) используя свойства логарифмов, преобразовать уравнение;
2) решить полученное уравнение;
3) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
log 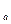f(х) = log 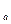g(х) 
f(x) = g(x) (f(x) >0 или g(x) > 0).
3. Уравнение второй и выше степени относительно логарифма.
Для решения таких уравнений надо:
1) сделать замену переменной;
2) решить полученное уравнение;
3) сделать обратную замену;
4) решить полученное уравнение;
5) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
4. Уравнения, содержащие неизвестное в основании и в показателе степени.
Для решения таких уравнений надо:
1) прологарифмировать уравнение;
2) решить полученное уравнение;
3)сделать проверку или найти область допустимых значений
для неизвестного числа и отобрать соответствующие им
корни (решения).
5. Уравнения, которые не имеют решения.
1) Для решения таких уравнений надо найти ОДЗ уравнения.
2) Проанализировать левую и правую часть уравнения.
3) Сделать соответствующие выводы.
Примеры:
log 
(4х+17) = log (4х- 3) + 1;
log (4х+17) = log 5(4х- 3);
4х + 17 = 5 (4х – 3);
ОДЗ: (4х+17)>0, (4х – 3) >0.
Ответ: 2.
log 
(х – 1) - log (2 х – 7) = 1 + 
(х – 4);
log (х – 1) = log (2х – 7) + log 2 - log (х – 4);
log (х – 1) + log (х – 4) = log ((2 х – 7) ∙ 2);
log ( (х – 1) ∙ (х – 4) ) = log ((2 х – 7) ∙ 2);
ОДЗ: х – 1>0; х – 4> 0; (2х – 7) > 0.
Ответ: 6.
lg (2х – 5) 
= 0;
lg (2х – 5) = lg 1;
(2х – 5) = 1;
х 
=3, х 
= 2.
Ответ: 2; 3.
Исходное уравнение равносильно системе:
log 
х > 0, log х ≠ 1, log х = 3 
х = 3 
.
Ответ: 3 .
Доказать, что уравнение не имеет решения.
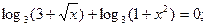
ОДЗ уравнения определяется неравенством х ≥ 0. На ОДЗ имеем
3 +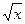 
≥ 3 и 1 + х ≥ 1;
Следовательно, log (3 + 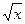) ≥ 1 и log (1 + х ) ≥ 0.
Сумма положительного числа и неотрицательного числа не равна нулю, поэтому исходное уравнение решений не имеет.
Ответ: решений нет.
ОДЗ: х > 0.
(log 4 + log х) - (log 2 + log х) + log х = 9;
4 + 4 log х + log 
х - log х - 2 log х – 1 + log х – 9 = 0;
log х – 2 = 0;
log х = 2;
х = 4. Ответ: 4.
3 log (х + 3) + 6 = 2 log (3 
-х) 
+ 2 log (х + 3 ) ;
ОДЗ: - 3 < х < 3 ; х ≠ - 3.
3∙ 2 log (х + 3) + 6 = 2∙ 3 log (3 - х) + 2∙ 3 log (3 + х);
log (х + 3) + 1 = log (3 -х) + log (3 +х);
log 2(х + 3) = log ( (3 -х) (3 + х) );
2 (х + 3) = (3 - х) (3 + х);
(2 (х + 3)) = (18 - х ) ;
2 (х + 3) = 18 - х или 2(х + 3) = - (18 - х ).
Ответ: -4; 
- 1.
log (х + 1) 
∙ log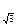 
(х + 3) = 3; ОДЗ: х > - 1;
3 log (х + 1) + 3 log (х + 3) = 3;
log (х + 1) + log (х + 3) = 1;
log [(х + 1) ∙(х + 3)] = 1;
(х + 1) ∙(х + 3) = 3;
х + 4х = 0;
х =0, х = -4.
В ОДЗ попадает только один корень х = 0.
Ответ: 0.
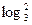х - log х 
- 7 = 0; ОДЗ: х >0;
9 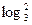х- 2 log х – 7 = 0.
Введем обозначение t = log х.
9t - 2t – 7 = 0;
t = 1, t = - 
.
Произведем обратную замену.
log х = 1, х = 3.
log х = - , х = 3 
.
Найденные корни принадлежат ОДЗ.
Ответ: 3; 3 
.
log 
+ 3log х + log 
х = 2;
ОДЗ уравнения – множество всех положительных чисел.
Поскольку
то исходное уравнение равносильно уравнению
Обозначим t = log 
х. Тогда последнее уравнение можно записать в виде 
t + t – 2 = 0 (t + 2) (t – 1) = 0 t = 1, t = -2.
Итак, данное уравнение на своей ОДЗ равносильно совокупности двух уравнений:
Ответ: 
Аналогично решаются данные уравнения:
1). 2log (х - 3) = log (х + 3) + log (х + 1) .
Ответ: -2.
2). log х - 5 log х + 87 = (
) + х .
Ответ: 9.
3). log 
х + log х – 1 = (
) + х .
Ответ: 0,125.