Например, водонапорные башни. У них основная масса сосредоточена наверху, поэтому водонапорную башню можно рассмотреть как систему с одной степенью свободы.
Дымовую трубу с равномерно распределенной массой нежелательно рассматривать как систему с одной степенью свободы, т.к. это приводит к большим погрешностям. Ее следует рассматривать как систему с большим числом степеней свободы.
Определение периодов, частот и форм собственных
Колебаний каркаса
Под частотой колебания системы понимается количество циклов колебаний, совершаемых системой в одну секунду. Период колебаний Т – это величина, обратная частоте, представляющая собой время, затраченное на совершение одного полного цикла колебаний.
Собственные формы колебаний отражают спектр частот и периодов, которыми обладает каркас здания. Название «собственные» связано с тем, что формы этих колебаний и соответствующие частоты определяются только собственными характеристиками системы: величинами и распределением масс, жесткостей, видом опор и т.д. Количество форм колебаний, которыми обладает каркас, равно числу степеней свободы масс. Однако в практических расчетах в целях упрощения можно принимать количество форм равным числу масс системы. Например, одномассовая система имеет одну форму колебания (рис. 1.5 а), двухмассовая – две (рис.1.5 б), четырехмассовая – четыре (рис. 1.5 в) и т.д.
Следует отметить, что для многомассовых систем при определении сейсмических сил допускается ограничить количество учитываемых форм. Согласно [1], для зданий и сооружений с простым конструктивно-планировочным решением при применении консольной расчётной модели усилия в конструкциях допускается определять с учётом не менее трёх форм собственных колебаний, если период первой (низшей) формы собственных колебаний значение Т1 более 0,4 с, и с учётом только первой формы, если значение Т1 равно или менее 0,4 с.
|
|
Для одномассовой системы период собственных колебаний, определяется по формуле:
, (1)
где 
- масса сооружения; Q– груз, сосредоточенный на уровне верха консоли;
g=.81 м/с2 – ускорение свободного падения;
- перемещение точки с массой m по направлению ее степени свободы от единичной силы, действующей в том же направлении, определяемое по формуле Мора с использованием единичной эпюры 
(рис. 1.6).
Рис.1.5. Формы колебаний:
а) одномассовая система;
б) двухмассовая система;
в) многомассовая система.
Рис.1.6. Формы колебаний:
а) расчетная динамическая модель здания;
б) деформированное состояние системы при действии единичной силы;
в) единичная эпюра моментов.
, (2)
где Н – длина консольного стержня;
- жесткость консольного стержня.
Также учитывая, что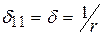 
[2,3], период собственных колебаний одномассовой системы может быть определен по формуле:
, (3)
где r – коэффициент жесткости консольного стержня; определяется по формуле:
. (4)
Для двухмассовой и многомассовой систем периоды (частоты) и формы собственных колебаний каркаса определяются на основе решения уравнений динамического равновесия системы [2, 3].
При расчете многоэтажных каркасных зданий при определении периодов колебаний можно использовать упрощенные формулы [6,7]:
|
|
- для зданий рамной системы:
, (5)
где i – номер формы колебаний (i = 1,2,3)
Н = Н 0 n/ (n- 0,5) – расчетная высота здания;
Н 0 - расстояние от обреза фундамента до оси ригеля верхнего этажа;
n – общее число этажей;
l= высота этажа;
m– масса яруса здания.
К – сила, вызывающая единичный угол перекоса здания, характеризующая сдвиговую жесткость многоэтажной рамы определяемая по формуле (15.147)[6]:
, (6)
s – сумма погонных жесткостей стоек одного этажа;
r – сумма погонных жесткостей ригелей одного этажа,
- для зданий связевой системы (см. формулу 15.162 [6]):
, (7)
где В – изгибная жесткость сплошной диафрагмы в своей плоскости;
ai - коэффициенты, определяемые по графику (рис. 15.52 [6]);
a 1 = 1,8; a 2 = 0,3; a 3 = 0,1.
Амплитуды колебаний или относительные смещения точек (масс) при собственных колебаниях динамической системы определяются путем решения уравнений ее динамического равновесия [2, 3]. В практических расчетах уравнения аппроксимируются в виде тригонометрических полиномов, и амплитуды колебаний можно найти по формуле:
Рис. 1.7.
|  (8)
где i – номер формы колебаний (i = 1,2,3,....);
j – номер расчетной точки (массы);
 - безразмерная координата точки j;
yj – положение точки j по вертикали относительно заделки.
Для одномассовой системы относительное смещение массы (груза) при собственных колебаниях  .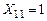
|