Д.ф.-м.н., проф. Блохин А.М.
Обыкновенные дифференциальные уравнения
Й и 4-й семестры, 2013/14 уч.год
Организационно-методический раздел.
1. Название курса: Обыкновенные дифференциальные уравнения. Курс обыкновенных дифференциальных уравнений с одной стороны является общематематической дисциплиной, а с другой стороны выступает как продолжение и дополнение к курсу математического анализа.
2. Цели и задачи курса. Дисциплина ”Обыкновенные дифференциальные уравнения” является основой для дальнейшего изучения таких разделов математики, как уравнения математической физики, функциональный анализ, вычислительная математика. С другой стороны, хорошие знания по этому курсу необходимы студентам, изучающим курсы теоретической механики, механики сплошной среды и т.д.
3. Требования к уровню освоения содержания курса. По окончанию изучения указанной дисциплины студент должен без труда уметь находить решения простейших обыкновенных дифференциальных уравнений.
4. Формы контроля. Для контроля усвоения дисциплины предусмотрен зачет (после 3-го семестра) и экзамен (после 4-го семестра). В течении каждого семестра выполняются контрольные работы (не реже 1-го раза в месяц), принимаются коллоквиумы (1-2 коллоквиума в семестр).
Содержание дисциплины.
1. Новизна курса: в целенаправленном использовании понятия матричной экспоненты при изложении материала курса.
2. Распределение часов.
Лекции: 68 часов.
Консультации: 27 часов.
Прием экзаменов: 48 часов.
Семинары: 68 часов.
Зачеты: 4 часа (на группу).
Проверка контрольных: 48 часов.
3. Содержание отдельных разделов и тем.
2.3.1 Линейные системы уравнений с постоянными коэффициентами. Единственность и существование решений у однородных уравнений. Пространство решений системы с постоянными коэффициентами и одного уравнения произвольного порядка. Фундаментальная система решений и определитель ее матрицы. Фундаментальная матрица и матричная экспонента. Вычисление матричной экспоненты для некоторых специальных матриц. Каноническое представление матричной экспоненты. Фундаментальные системы решений одного линейного уравнения с постоянными коэффициентами.
2.3.2 Система неоднородных линейных уравнений с постоянными
коэффициентами. Теорема о непрерывной зависимости решений от параметра.
2.3.3 Линейные системы уравнений с переменными коэффициентами. Априорная оценка решений. Существование и единственность решения задачи Коши. Основные свойства решений. Уравнение произвольного порядка с переменными коэффициентами.
2.3.4 Существование и единственность решений не обязательно линейных систем дифференциальных уравнений с достаточно гладкими правыми частями. Лемма Адамара. Обсуждение утверждений локальной теоремы существования. Достаточные условия для существования решений в целом.
2.3.5 Непрерывная дифференцируемая зависимость решений от параметра. Примеры на теорему о дифференцируемости решений по параметру.
2.3.6 Определение устойчивости и асимптотической устойчивости. Устойчивость и неустойчивость нулевого решения линейной системы в зависимости от расположения собственных значений. Матричное уравнение Ляпунова. Функции Ляпунова. Критерии устойчивости и неустойчивости.
2.3.7 Первые интегралы обыкновенных дифференциальных уравнений и уравнения в частных производных первого порядка. Представление общего решения линейного однородного уравнения с частными производными. Квазилинейные уравнения с частными производными. Уравнение Гамильтона-Якоби. Условие интегрируемости уравнений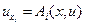 
, 
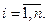
2.3.8 Краевые задачи для линейных систем уравнений первого порядка. Матрица Грина. Собственные значения. Ограниченные решения линейных неоднородных систем с постоянными коэффициентами. Краевые условия, удовлетворяющие условию Лопатинского. Линейное уравнение 2-го порядка.
Перечень примерных задач, позволяющих контролировать степень усвоения материала курса.
1. Докажите неравенства Куранта
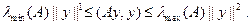
Здесь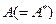 
- эрмитова матрица, 
, 
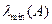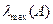- наименьшее и наибольшее
собственные значения матрицы A.
2. Найдите такие вектора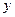 
, на которых достигаются равенства в левом и правом неравенствах
Куранта
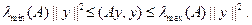
3. Докажите неравенство
где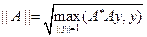 
- операторная норма матрицы A,
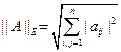- евклидова норма матрицы 
.
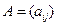4. Докажите неравенство
где 
- целое число.
5. Докажите неравенство
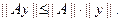
Здесь 
- квадратная матрица порядка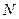 
.
6. Докажите, что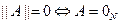 
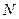. Здесь - квадратная матрица порядка , 
- нулевая матрица порядка .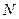
7. Построить векторный ряд для решения системы
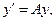
где
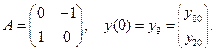
8. Построить векторный ряд для решения системы
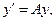
где
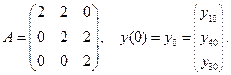
9. Доказать равномерную сходимость рядов
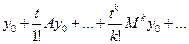
и
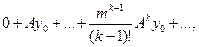
где 
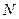- постоянный вектор, - матрица порядка с постоянными коэффициентами, 
.
10. Пусть
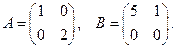
Покажите, что
11. Докажите неравенство треугольника
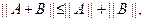
где , 
- квадратные матрицы порядка .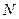
12. Покажите, что
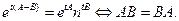
13. Пусть
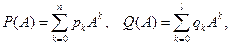
где 
, 
, 
, 
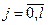- некоторые постоянные.
Покажите, что 
14. Докажите, что для любой матрицы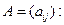 
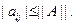
15. Доказать, что произведение двух верхних треугольных матриц будет снова верхней треугольной матрицей. Вывести отсюда утверждение, что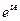 
, где - верхняя треугольная матрица, будет тоже верхней треугольной матрицей.
16. Показать, что решение Задача Коши для матричного уравнения
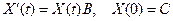
дается формулой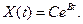 
17. Пусть (см. Теорему Шура)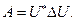 
Доказать, что
Здесь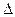 
- верхняя треугольная матрица.
18. Показать, что решение матричного уравнения
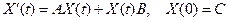
дается формулой
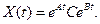
19. Покажите, что если уравнение с вещественными коэффициентами
имеет некратные корни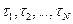 
, среди которых есть пара комплексно сопряженных 
, то в фундаментальной системе решений можно комплексные экспоненты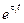 
, 
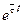заменить на вещественные решения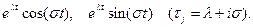 
20. Постройте для уравнения с вещественными коэффициентами и комплексными корнями вещественную фундаментальную систему, в случае, если среди корней есть кратные.
21. Покажите, что для уравнения с вещественными коэффициентами совокупность частных решений
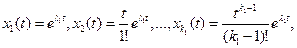
где 
является корнем кратности 
и т.д.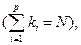 
образует фундаментальную систему решений.
22. Докажите, что матричная экспонента 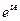непрерывно зависит от матрицы 
.
23. Пусть дана система
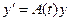
с непрерывными коэффициентами на отрезке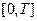 
. Известно, что на отрезке 
. Предполагая, что на отрезке 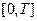существуют решение задачи
доказать, что
24. Даны матричные уравнения
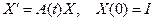
и
Показать, что
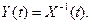
25. Известно, что любое решение Задачи Коши
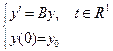
таково, что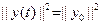 
. Показать, что это справедливо тогда и только тогда, когда 
(
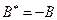-постоянная матрица).
26. Система
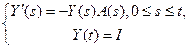
называется сопряженной по отношению к системе
Показать, что
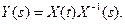
27. Показать, что решение матричного уравнения
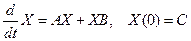
дается равенством
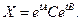
28. Пусть дано уравнени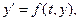е 
где
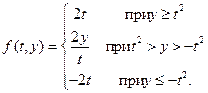
Убедитесь, что эта функция непрерывная (в том числе при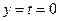 
). Докажите, что задача
Коши
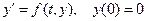
имеет бесконечно много решений. Почему?
29. Пусть дано уравнение 
, где
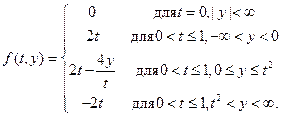
На множестве 
, 
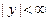функция 
непрерывна и ограничена постоянной:
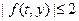(докажите). Докажите, что задача Коши 
не имеет решения.
Почему?
30. Задача Коши
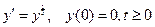
имеет решение 
.
Докажите, что решение этой задачи Коши не единственно.
31. Убедитесь, что для задачи
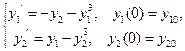
все решения стремятся к нулю при 
32. Рассмотрим задачу Коши
Докажите, что если функция 
непрерывно дифференцируема, то
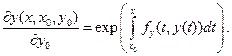
33. Докажите, что любая фундаментальная матрица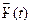 
системы 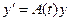может быть получена из любой другой 
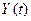умножением справа на некоторую невырожденную матрицу .
34. Докажите, что если
то задача
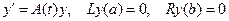
имеет только нулевое решение.
35. Для уравнения 
доказать, что колеблющееся решение не может иметь точки накопления нулей. Иными словами, все нули решения уравнения 
суть изолированные точки.
36. Пусть задано уравнение 
где коэффициент 
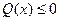при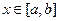 
. Тогда все решения уравнения не колеблющиеся на отрезке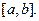 
37. Для системы
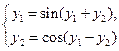
найти точки равновесия и исследовать их устойчивость.
38. Найти решение следующей задачи:
39. Найти решение следующей задачи:
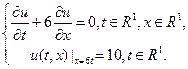
40. Найти решение следующей задачи:
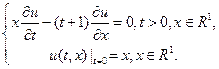
41. Найти время существования гладкого решения задачи:
- Учебно-методическое обеспечение дисциплины. Список основной и дополнительной литературы.
1. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.: Физматгиз, 1961.
2. Годунов С. К. Матричная экспонента, матрица Грина и условие Лопатинского. Новосибирск: НГУ, 1983.
3. Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: Наука 1970.
4. Годунов С. К. Квадратичные функции Ляпунова. Новосибирск: НГУ, 1982.
5. Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. М.: Наука 1973.
6. Годунов С. К и др. Сборник задач по обыкновенным дифференциальным уравнениям. Новосибирск: НГУ, 1986.
7. Блохин А. М. Равномерная ограниченность матричной экспоненты. Методические указания к курсу "Обыкновенные дифференциальные уравнения" Новосибирск: НГУ, 1986.
8. Блохин А. М. Элементы теории гиперболических систем и уравнений. Учебное пособие. Новосибирск: НГУ, 1995.
Изучение не предусматривает использование нормативно-правовых актов.
Проф., д.ф.-м.н. А. М. Блохин