Будем рассматривать твёрдое тело как систему жёстко связанных материальных точек с массой 
, и пусть ось вращения неподвижная. Для всякой системы материальных точек имеет место закон изменения суммарного момента импульса во времени:
Это уравнение справедливо и для твёрдого тела. В этом случае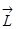 
- момент импульса тела, а справа стоит 
- сумма моментов внешних сил, действующих на тело, т.е.
- основной закон динамики вращения твёрдого тела
Если ось вращеня главная, то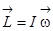 
, и получаем
,
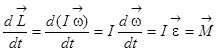т.е. 
- аналог второго закона Ньютона для
вращательного движения твёрдого тела
В случае главной оси вращения при суммарном моменте внешней силы, действующем на тело, равном нулю, имеет место закон сохранения момента импульса твёрдого тела:
- закон сохранения момента импульса твёрдого тела.
Если суммарный момент внешних сил 
, то он совершает работу, которая приводит к увеличению кинетической энергии вращающегося твёрдого тела (в этом случае потенциальная энергия 
).
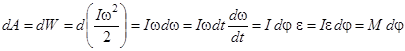
Итак 
- работа при вращении твёрдого тела
Вычислим также мощность при вращении твёрдого тела:
,
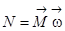- мощность при вращении твёрдого тела
Аналогия между поступательным и вращательным движением
| Поступательное движение | Вращательное движение |
s(t) - путь 
- линейная скорость
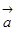- линейное ускорение
m - масса
- сила
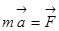- 2-ой закон
Ньютона
- импульс
-кинетическая
энергия
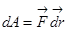-работа
-мощность 
- угол поворота
- угловая скорость
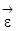- угловое ускорение
I - момент инерции
- момент силы
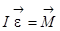- 2-ой закон Ньютона
для вращательного движения
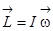- момент импульса
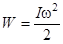- кинетическая
энергия вращающегося
твёрдого тела
|
|
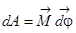- работа при
вращательном движении
- мощность при
| вращательном движении |
Из этого сопоставления легко заключить, что во всех случаях роль массы играет момент инерции, роль силы -момент силы, роль импульса -момент импульса, и т.д.
Гироскопы
Гироскопом (или волчком) называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. Эту ось будем называть осью гироскопа. Ось гироскопа является одной из главных осей инерции. Поэтому, если она не поворачивается в пространстве, момент импульса равен 
, где I -момент инерции относительно оси гироскопа.
При попытке вызвать поворот оси гироскопа наблюдается своеобразное явление, получившее название гироскопического эффекта: под действием сил, которые, казалось бы, должны вызвать поворот оси гироскопа ОО вокруг прямой 
(см. рисунок), ось гироскопа поворачивается вокруг прямой О''О'' направленной вдоль направления действия сил 
и 
. Поведение гироскопа оказывается полностью соответствующим законам динамики вращательного движения. Действительно, момент сил и направлен вдоль прямой О'О'. За время dt момент импульса гироскопа 
получит приращение 
, которое имеет такое же направление, как и . Спустя время dt момент импульса гироскопа будет равен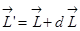 
и будет лежать в плоскости рисунка.. Таким образом, ось гироскопа повернётся вокруг прямой О''О'' на некоторый угол 
.
Из рисунка видно, что
,
Отсюда следует, что поворот оси гироскопа в новое положение произошел с угловой скоростью
.
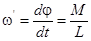Перепишем это соотношение в виде: 
|
|
Векторы , и 
взаимно перпендикулярны (вектор 
направлен вдоль прямой О’’О’’, на нас). Поэтому связь между ними можно записать в векторном виде:
.
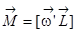Заметим, что эта формула справедлива лишь в том случае, если w’ << w
Допустим, что ось гироскопа может свободно поворачивается вокруг некоторой точки О (см. рисунок).
Рассмотрим поведение такого гироскопа в поле сил тяжести. Момент сил, приложенных к гироскопу, равен по величине: 
, где m - масса гироскопа, l - расстояние от точки О до центра инерции гироскопа, 
- угол, образованный осью гироскопа с вертикалью.
Под действием момента сил момент импульса получит за время dt приращение , перпендикулярное вектору .
При этом вертикальная плоскость, проходящая через ось гироскопа, повернётся на угол . Угол при этом не меняется.
Таким образом, в поле сил тяжести ось гироскопа с неподвижной точкой О поворачивается вокруг вертикали, описывая конус. Такое движение гироскопа называется прецессией Угловую скорость прецессии w’ можно найти, приняв во внимание полученное ранее соотношение
.
Подставляем сюда M, получим
, отсюда 
- угловая скорость прецессии.
Литература
Савельев И. В. Курс физики. Т. 1. Механика. Молекулярная физика. - М.: Наука, 1989. - 350 с.
Савельев И. В. Курс физики. Т. 2. Электричество и магнетизм. - М.: Наука, 1989. - 496 с.
Савельев И. В. Курс физики. Т. 3. Квантовая физика. - М.: Наука, 1989. - 301 с.
Сивухин Д. В. Механика. - М.: Физматлит, 2002. - 576 с.
Сивухин Д. В. Термодинамика и молекулярная физика. - М.: Физматлит, 2002. - 592 с.
Сивухин Д. В. Электричество. - М.: Физматлит, 2002. - 688 с.
|
|
Сивухин Д. В. Оптика. - М.: Физматлит, 2002. - 752 с.
Сивухин Д. В. Атомная физика. - М.: Физматлит, 2002.